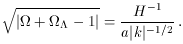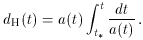2.5. Characteristic scales and horizons
The big bang Universe has two characteristic scales
The first of these gives the characteristic timescale of evolution of a(t), and the second gives the distance up to which space can be taken as having a flat (Euclidean) geometry. As written above they are both physical scales; to obtain the corresponding comoving scale one should divide by a(t). The ratio of these scales gives a measure of the total density; from the Friedmann equation we find
A crucial property of the big bang Universe is that it possesses horizons; even light can only have travelled a finite distance since
the start of the Universe t*, given by
For example, matter domination gives
dH(t) = 3t = 2H-1.
In a big bang Universe,
dH(t0) is a good approximation to
the distance to the surface of last scattering (the origin of the
observed microwave background, at a time known as `decoupling'), since
t0 >> tdec.