


3.4. Equations of motion and solutions
Let us assume there is only a single dynamical scalar field, and that
any extra contribution to the energy density from a second field is
included in its potential
V( ). The equations for an expanding
Universe containing a homogeneous scalar field are easily obtained by
substituting Eqs. (21) and (22) into the
Friedmann and fluid equations, giving
). The equations for an expanding
Universe containing a homogeneous scalar field are easily obtained by
substituting Eqs. (21) and (22) into the
Friedmann and fluid equations, giving
where prime indicates d /
d
Since
we will have inflation whenever the potential energy dominates. This
should be possible provided the potential is flat enough, as the
scalar field would then be expected to roll slowly.
The standard strategy for solving these equations is the slow-roll
approximation (SRA); this assumes that a term can be
neglected in each of the equations of motion to leave the simpler set
If we define slow-roll parameters
[6]
where the first measures the slope of the potential and the second the
curvature, then necessary conditions for the slow-roll approximation
to hold are (3)
Unfortunately, although these are necessary conditions for the
slow-roll approximation to hold, they are not sufficient, since even
if the potential is very flat it may be that the scalar field has a
large velocity. A more elaborate version of the SRA exists, based on
the Hamilton-Jacobi formulation of inflation
[7], which is
sufficient as well as necessary
[8].
Note also that the SRA reduces the order of the system of equations by
one, and so its general solution contains one less initial condition.
It works only because one can prove
[7,
8]
that the solution to
the full equations possesses an attractor property, eliminating the
dependence on the extra parameter.
3 Note that
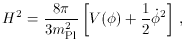
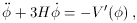
 . Here I have ignored the
curvature
term k, as it will quickly become negligible once inflation
starts. This is done for simplicity only; there is no obstacle to
including that term if one wished.
. Here I have ignored the
curvature
term k, as it will quickly become negligible once inflation
starts. This is done for simplicity only; there is no obstacle to
including that term if one wished.
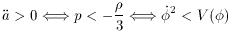
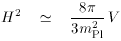
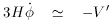
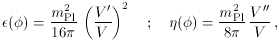
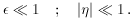
 is positive by definition,
whilst
is positive by definition,
whilst  can have
either sign. Back.
can have
either sign. Back.