


3.5. The relation between inflation and slow-roll
As it happens, the applicability of the slow-roll condition is closely connected to the condition for inflation to take place, and in many contexts the conditions can be regarded as equivalent. Let's quickly see why.
The inflationary condition
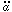 > 0 is satisfied for a much
wider range of behaviours than just (quasi-)exponential expansion. A
classic example is power-law inflation
a
> 0 is satisfied for a much
wider range of behaviours than just (quasi-)exponential expansion. A
classic example is power-law inflation
a  tp for p > 1,
which is an exact solution for an exponential potential
tp for p > 1,
which is an exact solution for an exponential potential
We can rewrite the condition for inflation as
where the last manipulation uses the slow-roll approximation. The
final condition is just the slow-roll condition
Inflation will occur when the slow-roll conditions are satisfied
(subject to some caveats on whether the `attractor' behaviour has been
attained [8]).
However, the converse is not strictly true, since we had to use the
SRA in the derivation. However, in practice
The last condition arises because unless the curvature of the
potential is small, the potential will not be flat for a wide enough
range of 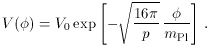
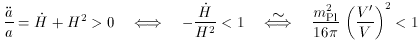
 < 1, and
hence
< 1, and
hence
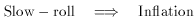
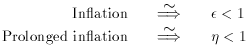
 .
.