


3.7. A worked example: polynomial chaotic inflation
The simplest inflation model
[9]
arises when one chooses a
polynomial potential, such as that for a massive but otherwise
non-interacting field,
V( ) =
m2
) =
m2 2 / 2
where m is the mass
of the scalar field. With this potential, the slow-roll equations are
2 / 2
where m is the mass
of the scalar field. With this potential, the slow-roll equations are
and the slow-roll parameters are
So inflation can proceed provided
|
The slow-roll equations are readily solved to give
(where
This last equation can be obtained from the solution for a, but in
fact is more easily obtained directly by integrating
Eq. (32), for which one needn't have bothered to solve the
equations of motion.
In the older inflationary literature, it was typically assumed that in
order for classical physics to be valid, we would require
V << mPl4 but no other restriction
would be necessary. In particular,
considering scalar field theory in flat space-time, there is no
particular meaning to the actual value of the scalar field (which for
instance could be shifted by a constant). With those presumptions, we
see that while sufficient inflation requires
|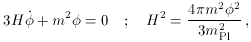
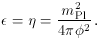
 | > mPl /
| > mPl /
 (4
(4
 ), i.e. as
long as we are not too close to the minimum.
), i.e. as
long as we are not too close to the minimum.
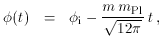
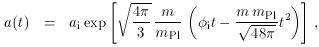
 =
=
 i
and a = ai at t = 0) and the
total amount of inflation is
i
and a = ai at t = 0) and the
total amount of inflation is
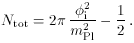
 | > mPl,
one can readily get enough inflation provided m is small enough, and
indeed we will see later that m is in fact required to be small from
observational limits on the size of density perturbations produced,
allowing far more than the minimum amount of inflation required to
solve the various cosmological problems we originally set out to
solve.
| > mPl,
one can readily get enough inflation provided m is small enough, and
indeed we will see later that m is in fact required to be small from
observational limits on the size of density perturbations produced,
allowing far more than the minimum amount of inflation required to
solve the various cosmological problems we originally set out to
solve.