


3.7.1. Multi-field theories
While much of early investigation of inflation featured potentials
such as the massive field discussed above, such models are widely
regarded by inflation model builders as unsatisfactory. The reason is
that current thinking in particle physics is dominated by
supersymmetry, implying that in a cosmological context we should be
operating within the framework of supergravity. Once supergravity is
brought into play, the numerical value of the scalar field acquires a
well-defined meaning, and it is believed that its value must be less
than the (reduced) Planck mass
mPl /
 (8
(8
 ) if the
potential is not to be vulnerable to large nonrenormalizable
corrections, which typically will destroy slow-roll and anyway will
render theoretical calculations unreliable. As we have just seen, one
cannot obtain sufficient inflation (or indeed any at all) with the
polynomial potential under this restriction, and this conclusion is
fairly generic for models where there is only a single scalar field.
) if the
potential is not to be vulnerable to large nonrenormalizable
corrections, which typically will destroy slow-roll and anyway will
render theoretical calculations unreliable. As we have just seen, one
cannot obtain sufficient inflation (or indeed any at all) with the
polynomial potential under this restriction, and this conclusion is
fairly generic for models where there is only a single scalar field.
An attractive way of circumventing this problem is the hybrid inflation model [10], where a second field provides an additional energy density which dominates over that from the inflaton itself. A typical potential takes the form
where g2 is the coupling constant governing the
interaction between
the two fields. This is shown in Fig. 1. For large
inflaton values the coupling stabilizes
The interesting case is where the constant term dominates, as it
provides extra friction to the
Figure 1. The potential for the hybrid
inflation model. The field rolls down the channel at
The original models
[10]
assumed that the inflaton potential
V(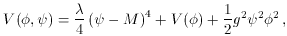
 at zero, where it
contributes a potential energy
at zero, where it
contributes a potential energy
 M4 / 4 but
otherwise does not
participate in the dynamics, so that the inflaton sees a potential
M4 / 4 but
otherwise does not
participate in the dynamics, so that the inflaton sees a potential
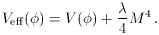
 equation of motion which makes
it roll much more slowly, enabling sufficient inflation without
violating the condition
equation of motion which makes
it roll much more slowly, enabling sufficient inflation without
violating the condition
 << mPl /
<< mPl /
 (8
(8
 ). Inflation
ends when the
). Inflation
ends when the  field drops below a
critical value, destabilizing
the
field drops below a
critical value, destabilizing
the  field and allowing the system
to rapidly evolve into its
true minimum at
field and allowing the system
to rapidly evolve into its
true minimum at  = 0,
= 0,
 = ±M.
= ±M.
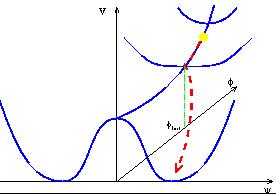
 = 0 until
it reaches the critical
= 0 until
it reaches the critical  value,
then falls off the side to the
true minimum at
value,
then falls off the side to the
true minimum at  = 0 and
= 0 and
 = ±M.
= ±M.
 ) was just that of a
massive field, but unfortunately this
choice is vulnerable to large loop corrections which dominate over the
mass term. However many other possible models have been derived within
the hybrid framework; for an extensive discussion of this and other
model-building issues see the review of Lyth and Riotto
[11].
) was just that of a
massive field, but unfortunately this
choice is vulnerable to large loop corrections which dominate over the
mass term. However many other possible models have been derived within
the hybrid framework; for an extensive discussion of this and other
model-building issues see the review of Lyth and Riotto
[11].