


4.3. Observational consequences
Observations have moved on beyond us wanting to know the overall normalization of the potential. The interesting things are
These can be neatly summarized using the slow-roll parameters
 and
and  we defined
earlier
[6].
we defined
earlier
[6].
The standard approximation used to describe the spectra is the power-law approximation, where we take
where the spectral indices n and
nG are given by
The power-law approximation is usually valid because only a limited
range of scales are observable, with the range 1 Mpc to 104 Mpc
corresponding to
The crucial equation we need is that relating
(since within the slow-roll approximation
k
where now
Finally, we need a measure of the relevant importance of density
perturbations and gravitational waves. The natural place to look is
the microwave background; a detailed calculation which I cannot
reproduce here (see e.g. Ref.
[18]) gives
Here the Cl are the contributions to the microwave
multipoles, in the usual notation.
(5)
From these expressions we immediately see
At present, a large number of inflationary models exist covering a
large part of the n-r parameter space. Observations are just
beginning to narrow down the allowed region, and in the future
satellite microwave anisotropy experiments such as MAP and Planck
[20]
should determine n sufficiently accurately to exclude
almost all models of inflation on that basis, and may be able to
measure r as well.
The principal observational challenge is to untangle the effects of
the inflationary parameters
(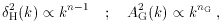
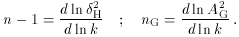
 ln k
ln k
 9.
9.
 values to when a scale
k crosses the Hubble radius, which from Eq. (43) is
values to when a scale
k crosses the Hubble radius, which from Eq. (43) is
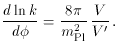
 exp N). Direct
differentiation then yields
[6]
exp N). Direct
differentiation then yields
[6]
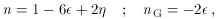
 and
and
 are to be evaluated
on the appropriate part of the potential.
are to be evaluated
on the appropriate part of the potential.
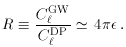
 << 1 and
|
<< 1 and
| | << 1 do we get
n
| << 1 do we get
n  1 and
R
1 and
R  0.
0.
 is quite a bit smaller than one.
is quite a bit smaller than one.
 H(k0), n and r)
from all the
other parameters required to specify a complete cosmological model,
such as the Hubble constant, the density of each component of matter,
and so on. The two sets of parameters cannot be studied separately; an
attempt to match the observations must fit for both simultaneously. A
typical set of parameters likely to be important in determining
predictions for observations such as microwave anisotropies contains
about ten different parameters, with some authors suggesting this list
extends up to fifteen or more. It is a testament to the predicted
accuracy of upcoming observations that considerable progress is
expected in this direction over the next decade.
H(k0), n and r)
from all the
other parameters required to specify a complete cosmological model,
such as the Hubble constant, the density of each component of matter,
and so on. The two sets of parameters cannot be studied separately; an
attempt to match the observations must fit for both simultaneously. A
typical set of parameters likely to be important in determining
predictions for observations such as microwave anisotropies contains
about ten different parameters, with some authors suggesting this list
extends up to fifteen or more. It is a testament to the predicted
accuracy of upcoming observations that considerable progress is
expected in this direction over the next decade.