


4.2. A worked example
The easiest way to see what is going on is to work through a specific
example, the
m2 2 /
2 potential which we already saw in
Section 3.7. We'll see that we don't even have to
solve the evolution equations to get our predictions.
2 /
2 potential which we already saw in
Section 3.7. We'll see that we don't even have to
solve the evolution equations to get our predictions.
 = 1, so
= 1, so
 end
end
 mPl /
mPl /
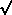 (4
(4 ).
).
 60
60
 3mPl.
3mPl.
 H
H
 2 x 10-5
(provided AG <<
2 x 10-5
(provided AG <<
 H), so we need
m
H), so we need
m  10-6mPl.
10-6mPl.
Because the required value of m is so small, that means it is easy
to get sufficient inflation to solve the cosmological problems if one
only requires the classicality condition
V < mPl4. Since that
condition implies only that  <
mPl2 / m
<
mPl2 / m
 106mPl, and as
Ntot
106mPl, and as
Ntot  2
2
 2 /
mPl2, we can get up to about
1013 e-foldings in principle. This compares extremely
favourably with the 70 or so actually required.
2 /
mPl2, we can get up to about
1013 e-foldings in principle. This compares extremely
favourably with the 70 or so actually required.