


5.1. Cosmological constant: exact or effective?
The discovery of strong evidence that the present Universe is accelerating is one of the most striking discoveries of recent cosmology. The results from Type Ia supernovae have been confirmed by two separate teams [26], and have subsequently stood up to detailed examination of the underlying mechanisms. The general conclusion has been further bolstered by support [1, 2] from the microwave background for the expectation that the Universe is spatially flat, which coupled with the observed low matter density gives independent demonstration of the need for a cosmological constant or similar.
These developments have confirmed the
 CDM model as the
standard cosmological model. It has a matter density around one third
of the critical density, with the cosmological constant making up the
remainder. It explains a range of phenomena concerning the observed
content and dynamics of the Universe (including the age and the
observed acceleration), and provides a model of structure formation
which is not in serious disagreement with any existing
observations. It is accepted almost universally amongst cosmologists
that this model is currently the most observationally viable.
CDM model as the
standard cosmological model. It has a matter density around one third
of the critical density, with the cosmological constant making up the
remainder. It explains a range of phenomena concerning the observed
content and dynamics of the Universe (including the age and the
observed acceleration), and provides a model of structure formation
which is not in serious disagreement with any existing
observations. It is accepted almost universally amongst cosmologists
that this model is currently the most observationally viable.
Despite that, the fraction of cosmologists willing to accept the
 CDM model is significantly
less, because of serious
philosophical objections to the idea of a cosmological constant. First
of all, there is absolutely no fundamental understanding of the
cosmological constant. The standard interpretation is that it
corresponds to the energy density of the vacuum state, but attempts to
compute it typically result in answers so large as to be immediately
excluded, leading to the suspicion that some as-yet-unknown physical
mechanism sets it precisely to zero. This is known as the cosmological
constant problem. Secondly, that the cosmological constant has just
come to dominate at the present epoch marks out this time as a special
point in the Universe's history; at a redshift of a few it was
completely negligible, and within a Hubble time it will be completely
dominant. As the historical theme of cosmology has been to avoid
placing ourselves at preferred locations both spatially and
temporally, this situation causes great unease and has become known as
the coincidence problem.
CDM model is significantly
less, because of serious
philosophical objections to the idea of a cosmological constant. First
of all, there is absolutely no fundamental understanding of the
cosmological constant. The standard interpretation is that it
corresponds to the energy density of the vacuum state, but attempts to
compute it typically result in answers so large as to be immediately
excluded, leading to the suspicion that some as-yet-unknown physical
mechanism sets it precisely to zero. This is known as the cosmological
constant problem. Secondly, that the cosmological constant has just
come to dominate at the present epoch marks out this time as a special
point in the Universe's history; at a redshift of a few it was
completely negligible, and within a Hubble time it will be completely
dominant. As the historical theme of cosmology has been to avoid
placing ourselves at preferred locations both spatially and
temporally, this situation causes great unease and has become known as
the coincidence problem.
The observed value of the cosmological constant is that it is close to the critical density, which in particle physics units gives
The naïvest fundamental physics estimates of the vacuum energy
assume no suppression of contributions to the vacuum energy all the
way to the Planck scale, and thus yield
For an early Universe cosmologist, the temptation is irresistible to
try and employ the same physical mechanisms in the present Universe as
we did for inflation in the early Universe. Both correspond to an
acceleration of Universe, and both could be the consequence of
domination of the Universe's energy density by the potential energy of
a scalar field. Because we know, for example from nucleosynthesis,
that there must have been a longer deceleration phase in between these
two epochs, with some notable exceptions
[27] the standard
assumption is that different scalar fields are responsible for the two
epochs, but that the physical mechanism is analogous. Describing the
cosmological constant as an effective one via a scalar field has
become known as quintessence, though that is a recent term to
describe an idea with quite a long history
[28,
29].
As far as modelling is concerned, there are some differences between
the early Universe and today. In the early Universe, we know that
inflation has to come to an end, and arranging that this happens
satisfactorily is a significant constraint on model building. By
contrast, we have no idea whether the present acceleration will end in
the future. Secondly, in the present Universe we are interested in the
earliest stages of the acceleration, and indeed the way in which the
Universe entered the accelerating phase, and so we cannot neglect the
effect of the non-scalar field matter as is common in early Universe
inflation studies.
Broadly speaking, one can recognize three different possibilities. One
is that in our Universe the scalar field is in the true minimum of its
potential, whose value happens to be non-zero. Phenomenologically this
is no different from a true cosmological constant. Secondly, we might
live in a metastable false vacuum state, destined at some future epoch
to tunnel into the true vacuum. Such tunnelling would almost certainly
have drastic consequences for the material world, but we can be
somewhat reassured by the fact that the decay time is at least a
Hubble time. The false vacuum in this case also mimics a cosmological
constant. Neither of these scenarios give us the possibility of
addressing the coincidence problem, so mostly attention has been
focussed on the third possibility, that the scalar field is slowly
rolling in its potential akin to the chaotic inflation models. In this
situation, the effective cosmological constant is in fact not constant
at all but rather is slowly varying, and as such observations can seek
to distinguish it from a pure cosmological constant.
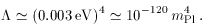

 mPl4. Reasonable arguments can bring this
down to the scale of
supersymmetry,
mPl4. Reasonable arguments can bring this
down to the scale of
supersymmetry,
 =
msusy4
=
msusy4  10-64 mPl4, by
presuming that at energies where supersymmetry is restored
the bosonic and fermionic contributions to the cosmological constant
cancel exactly. The vast discrepancy between expectation and reality
puts us in an awkward situation; either we have to find an argument
for a dimensionless prefactor to that estimate making up the remaining
factor of 10-56, or we might conclude that there must be some
fundamental principle setting it to zero leaving us to look elsewhere.
10-64 mPl4, by
presuming that at energies where supersymmetry is restored
the bosonic and fermionic contributions to the cosmological constant
cancel exactly. The vast discrepancy between expectation and reality
puts us in an awkward situation; either we have to find an argument
for a dimensionless prefactor to that estimate making up the remaining
factor of 10-56, or we might conclude that there must be some
fundamental principle setting it to zero leaving us to look elsewhere.