


5.2. Scaling solutions and trackers
One reason for having optimism that quintessence can at least address
the coincidence problem comes from an interesting class of solutions
known as scaling solutions or trackers. These arise because the scalar
field does not have a unique equation of state
p  p(
p( ). Although
we can usefully define an effective equation of state
). Although
we can usefully define an effective equation of state
in which terminology cosmological constant behaviour corresponds to
w = - 1, the scalar field velocity depends on the Hubble
expansion, which in turn depends not only on the scalar field itself but on the
properties of any other matter that happens to be around. That is to
say, the scalar field responds to the presence of other matter.
A particularly interesting case is the exponential potential
which we already saw in the early Universe context as
Eq. (30). If there is only a scalar field present, this
model has inflationary solutions
a
Unfortunately this is not good enough. We don't want the scalar field
to be behaving like matter at the present, since it is supposed to be
driving an acceleration, and we need it to be negligible in the fairly
recent past. This requires us to consider alternatives to the
exponential potential, a common example being the inverse power-law
potential
[28]
where
With negative
This type of scenario can give a model capable of explaining the
observational data, though it turns out that quite a shallow power-law
is required in order to get the field to be behaving sufficiently like
a cosmological constant (current limits require
w
Various other forms of the potential have been experimented with, and
many possibilities are known to give viable evolution histories
[33].
While such models do give a framework for interpretting
the type Ia supernova results, in many cases with the possibility
ultimately of being distinguished from a pure cosmological constant, I
believe it is fair to say that so far no very convincing resolution of
either the cosmological constant problem or the coincidence problem
has yet appeared. However, quintessence is currently the only approach
which has any prospect of addressing these issues.
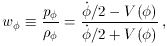
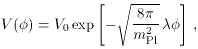
 t2/
t2/ 2 for
2 for
 2 < 2, and
non-inflationary power-law solutions
otherwise. However, if we add conventional matter with equation of state
p = w
2 < 2, and
non-inflationary power-law solutions
otherwise. However, if we add conventional matter with equation of state
p = w ,
a new class of solutions can arise, which turn out
to be attractors whenever they exist
[28,
29,
30]. These
solutions take the form of scaling solutions, where the scalar field
energy density (indeed both its potential and kinetic energy density
separately) exhibit the same scaling with redshift as the conventional
matter. That is to say, the scalar field mimics whatever happens to be
the dominant matter in the Universe. So, for example, in a
matter-dominated Universe, we would find
,
a new class of solutions can arise, which turn out
to be attractors whenever they exist
[28,
29,
30]. These
solutions take the form of scaling solutions, where the scalar field
energy density (indeed both its potential and kinetic energy density
separately) exhibit the same scaling with redshift as the conventional
matter. That is to say, the scalar field mimics whatever happens to be
the dominant matter in the Universe. So, for example, in a
matter-dominated Universe, we would find


 1/a3. If
the matter era were preceded by a radiation era, at that time the
scalar field would redshift as 1/a4, and it would make
a smooth
transition between these behaviours at equality. The ratio of
densities is decided only by the fundamental parameters
1/a3. If
the matter era were preceded by a radiation era, at that time the
scalar field would redshift as 1/a4, and it would make
a smooth
transition between these behaviours at equality. The ratio of
densities is decided only by the fundamental parameters
 and
w. So, at any epoch one expects the scalar field energy density to
be comparable to the conventional matter.
and
w. So, at any epoch one expects the scalar field energy density to
be comparable to the conventional matter.
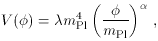
 < 0. In fact, Liddle
and Scherrer
[31] gave a
complete classification of Einstein gravity models with scaling
solutions, defined as models where the scalar field potential and
kinetic energies stay in fixed proportion. The exponential potential
is a particular case of that, but in general the scaling of the
components of the scalar field energy density need not be the same as
the scaling of the conventional matter, and indeed the inverse
power-law potential is an example of that; if the conventional matter
is scaling as 1/am where m = 3(1 + w),
there is an attractor solution
in which the scalar field densities will scale as
< 0. In fact, Liddle
and Scherrer
[31] gave a
complete classification of Einstein gravity models with scaling
solutions, defined as models where the scalar field potential and
kinetic energies stay in fixed proportion. The exponential potential
is a particular case of that, but in general the scaling of the
components of the scalar field energy density need not be the same as
the scaling of the conventional matter, and indeed the inverse
power-law potential is an example of that; if the conventional matter
is scaling as 1/am where m = 3(1 + w),
there is an attractor solution
in which the scalar field densities will scale as
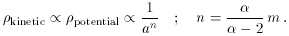
 , the scalar
field energy density is redshifting
more slowly and eventually overcomes the conventional matter, at which
point the Universe starts to accelerate.
, the scalar
field energy density is redshifting
more slowly and eventually overcomes the conventional matter, at which
point the Universe starts to accelerate.
 < - 0.6 at the
present epoch, where
< - 0.6 at the
present epoch, where 

 0.7
[32]). Also, the
epoch at which the field takes over and drives an acceleration is
still more or less being put in by hand; it turns out that the
acceleration takes over when
0.7
[32]). Also, the
epoch at which the field takes over and drives an acceleration is
still more or less being put in by hand; it turns out that the
acceleration takes over when

 mPl, and so
mPl, and so

 10-120 is required
to ensure this epoch is delayed until the present.
10-120 is required
to ensure this epoch is delayed until the present.