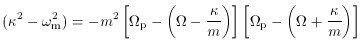3.3. Dynamics of barred galaxies
The central problem in the dynamics of spiral galaxies is the understanding of the origin and evolution of the spiral and barred structures that appear with a range of shapes in these partly stellar, partly gaseous systems, where young stars are continuously being born out of the gas. In particular, these structures appear to be long-lived in spite of the presence of a shearing velocity field where the angular velocity of rotation varies with distance from the centre. This led to the idea that the observed structure is the manifestation of a density wave rather than a material configuration.
In the early 1960s B. Lindblad (1963, 1964) suggested a circulation theory of spiral structure, where due to the gravitational forces of the spiral arms matter would circulate between the arms and create a self-supporting quasi-permanent spiral structure. Lin and Shu (1964) linearized the problem and formulated a theory for self-consistent tightly wound spiral stellar density waves. (For a recent review of the density wave theory see Bertin & Lin 1996.) This triggered a large amount of work in this field (see Toomre 1977 for a review) and a picture emerged where the circulating interstellar matter was strongly compressed in the potential well of the spiral arms and there created young stellar associations which ionize the gas to form H II regions and then leave the arms with increasing age. The extent of the spiral structure was governed by a series of resonances between orbital motion and the rotating potential.
However, the barred galaxies pose a somewhat different problem and, as a matter of fact, it seems that when considering the origin and maintenance of structures of galaxies our understanding is more complete for the barred galaxies. Sellwood and Wilkinson (1993) have reviewed in a very comprehensive way our present understanding of the dynamics of barred galaxies. Numerous numerical N-body simulations have shown that a rotationally supported stellar disk of a certain flatness is strongly unstable to the formation of a bi-symmetric stellar bar running through the centre and rotating with a certain pattern angular velocity. These numerical results are supported by stability analyses which lead to the study of normal modes of an axisymmetric stellar disk. The dominant modes found in these studies grow fast and have an open bi-symmetric S-shape. The numerical N-body simulations show that this modal bar straightens up and as time goes on ends just inside the Lagrange points on the bar major axis (defining the so called co-rotation radius), while the originally formed weak trailing spiral arms extending from the ends of the bar are transient and fade away. It seems likely that the formation of the disk and the bar are not two separate events, as assumed in most simulations, but are in fact intimately coupled (Sellwood & Wilkinson 1993). As suggested by Ostriker and Peebles (1973) a massive halo may check this bar instability. However, as pointed out by Sellwood and Wilkinson, there are reasons why this checking mechanism does not seem to work in spiral galaxies.
The bar potential affects the dynamics of the rest of the system and there are numerous studies of orbits in rotating bar potentials. The majority of stars within the bar seem to follow epicyclic orbits, trapped around elongated closed (in the frame rotating with the bar) periodic orbits aligned with the bar. The gaseous component, due to internal friction, reacts in a different way. When gas pressure is neglected, the gas stream lines must nearly coincide with the stellar periodic orbits. Gas stream lines are not permitted to intersect and large scale shocks may develop when the perturbing potential becomes strong. As shown by hydrodynamical calculations (e.g. Sanders & Huntley 1976) the flow pattern settles down to a density wave which is steady in the rotating frame of the bar. The dominating shape is a trailing spiral structure, which is governed by the series of main resonances in the system.
To understand the nature of these resonances, let us assume that the
differential rotation of the disk in the presence of a weak bar is
described by the circular angular velocity as a function of the radius
 (R) and that the
perturbing bar potential rotates as a solid
body with the pattern angular velocity
(R) and that the
perturbing bar potential rotates as a solid
body with the pattern angular velocity
 p. The most
fundamental resonance occurs where the circular angular velocity equals
the angular velocity of the bar, i.e.
p. The most
fundamental resonance occurs where the circular angular velocity equals
the angular velocity of the bar, i.e.
 =
=
 p. This
is the corotation resonance.
p. This
is the corotation resonance.
In a non-circular orbit a particle oscillates in the radial direction
with a frequency, which we will denote by
 , and which is a
function of the mean radius and the amplitude of the radial motion. Such
an orbit can always be transferred into a closed periodic orbit by
introducing a rotating coordinate system. If we choose the closed orbit
to have m apocentra, the angular velocity of this coordinate system is
, and which is a
function of the mean radius and the amplitude of the radial motion. Such
an orbit can always be transferred into a closed periodic orbit by
introducing a rotating coordinate system. If we choose the closed orbit
to have m apocentra, the angular velocity of this coordinate system is
 -
-
 /m or
/m or
 +
+
 /m, depending on whether the
particle should describe the closed orbit in the direct or retrograde
direction. For a bar with its two-fold symmetry the fundamental
resonances occur when
/m, depending on whether the
particle should describe the closed orbit in the direct or retrograde
direction. For a bar with its two-fold symmetry the fundamental
resonances occur when
Resonances with values of m other than 2 will arise due to other order
Fourier components in the development of the bar potential. Such
resonances also arise due to the non-linear nature of the problem (so
called ultra- or hyper-harmonic resonances).
If the radial amplitude is small,
The prime effect of the bar on stellar orbits is to enhance their
radial amplitudes, in particular in the neighbourhood of resonances. In
the case of m = 2, closed stellar orbits will be elongated along the
bar or at right angles to the bar depending on the position with
respect to the resonances and the relative rate of radial change of the
bar potential. At each resonance the phase of the oscillation and the
orientation of the orbit in this case will shift by
We will give a more mathematical illustration as follows using the
epicyclic approximation with some simplifying assumptions (see
Lindblad & Lindblad 1994;
Wada 1994).
Consider an orbit that does not deviate
much from a circular orbit with radius Ro, and introduce a
coordinate system rotating with the angular velocity of circular motion
where m only takes even values.
To simulate gas dynamics we introduce a frictional force proportional to
the deviation from circular motion at the position of the particle and
with a damping coefficient
where Oort's constant A = -1/2 R
d
where
and
The solution given by (4) and (5) represents the
forced oscillation due to the perturbing potential.
As
we see that the amplitudes get large for the resonance conditions for
the ILR and OLR mentioned above. Also, when passing across a resonance
the orientation of the closed orbit turns smoothly by close to
180°/m.
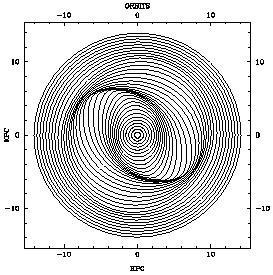
This is illustrated in Fig. 12 where the exact
solution to Eqs. (2) and (3) has been used and the bi-symmetric bar has
been modeled from the bar of NGC 1365 (see
Section 3.4). The
axisymmetric component of the potential, however, is chosen to give a
strictly flat rotation curve with a clearcut single ILR at a distance of
6.7 kpc from the centre. As can be seen, the innermost elongated gas
orbits are oriented close to perpendicular to the (horizontal) bar. When
approaching the ILR the amplitude increases and the orbits twist in the
counter-clockwise direction until outside the resonance they tend to be
elongated along the bar. The result is a trailing spiral density wave
pattern. With increasing strength of the bar, the amplitudes increase
until the orbits touch and large-scale shocks develop along the leading
side of the bar.
Figure 12. Closed gas orbits in a barred
potential computed analytically in the epicyclic approximation. The bar
is horizontal and the rotation is clockwise. The ILR is at 6.7 kpc from
the centre.
Lindblad and Lindblad
(1994)
as well as Wada (1994)
compared the
results given by the linear epicyclic approximation with
numerical hydrodynamic calculations demonstrating the general
agreement. The linear
approximation is a useful tool to give insight into the orbital structures and
to very quickly scan the multi-dimensional parameter space. However,
this simple approximation fails around corotation where closed stellar
orbits tend to circulate around Lagrange points and the gas response
seems to be rather dependent on the self-gravity of the gas
(Section 3.4).
Sellwood and Sparke
(1988)
introduce a complication to this picture of
a completely bar driven spiral structure. They note that in a number of
N-body simulations an outer spiral structure appears with a pattern
speed much lower than that of the bar. They argue that barred galaxies
with well-developed outer spiral structure must have spiral density
waves in the stellar component which are driven by some other mechanism
than a steady bar and thus could well have a pattern speed different
from that of the bar. As far as observations go they mention NGC 1365
as giving supporting evidence and
Sellwood and Wilkinson
(1993)
even state that the most convincing evidence for two separate pattern speeds
in a galaxy is given by NGC 1365.
P.A.B. Lindblad et
al. (1996)
find no need for two pattern speeds in NGC 1365 and we will further
discuss this question in Section 3.4.
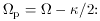 the so-called Inner Lindblad
(1) Resonance (ILR),
the so-called Inner Lindblad
(1) Resonance (ILR),
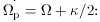 the so-called Outer Lindblad Resonance (OLR).
the so-called Outer Lindblad Resonance (OLR).
 can be considered as a
function of R only. Fig. 13
shows the rotation curve,
i.e. circular velocity as a function of R, which we later will adopt
for NGC 1365, as well as the functions
can be considered as a
function of R only. Fig. 13
shows the rotation curve,
i.e. circular velocity as a function of R, which we later will adopt
for NGC 1365, as well as the functions
 and
and
 °
°  /m, where
m = 2, 4, and 6. The horizontal line, representing
the pattern angular velocity
/m, where
m = 2, 4, and 6. The horizontal line, representing
the pattern angular velocity
 p, then gives the positions
of the corresponding resonances.
p, then gives the positions
of the corresponding resonances.
 /2 with
respect to the bar (in analogy with the forced oscillation of a
pendulum, where the phase of the oscillation shifts by
/2 with
respect to the bar (in analogy with the forced oscillation of a
pendulum, where the phase of the oscillation shifts by
 at the
resonance frequency). If, however, dissipative forces are present as in
the gas dynamical case, the amplitudes will be damped and the
orientation of the closed orbits of the gas will deviate from that of
the bar and gradually twist when passing over a resonance and thereby
form a spiral density wave pattern.
at the
resonance frequency). If, however, dissipative forces are present as in
the gas dynamical case, the amplitudes will be damped and the
orientation of the closed orbits of the gas will deviate from that of
the bar and gradually twist when passing over a resonance and thereby
form a spiral density wave pattern.
 (Ro). The deviation
from circular motion at R = Ro is given by the
coordinates
(Ro). The deviation
from circular motion at R = Ro is given by the
coordinates  in the
radial direction and
in the
radial direction and
 along the circular
arc with radius Ro. We assume a
perturbing bisymmetric bar potential
along the circular
arc with radius Ro. We assume a
perturbing bisymmetric bar potential
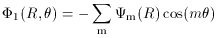
 is the angular distance from
the bar potential minimum. This bar is supposed to rotate with the
angular velocity
is the angular distance from
the bar potential minimum. This bar is supposed to rotate with the
angular velocity
 p, and we introduce
p, and we introduce
 m(R) as the
frequency with which a
particle in circular orbit encounters the potential minimum of a
certain Fourier component, i.e.
m(R) as the
frequency with which a
particle in circular orbit encounters the potential minimum of a
certain Fourier component, i.e.
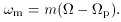
 . Assuming that we are not
close to corotation the equations of motion in the linear epicyclic
approximation are
. Assuming that we are not
close to corotation the equations of motion in the linear epicyclic
approximation are
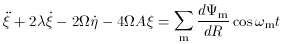
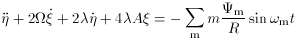
 / dR. All
quantities dependent on R are to be evaluated at R =
Ro. We choose Ro to be the radius of the
circular orbit described by the guiding centre of the final
orbit. Further we assume
that
/ dR. All
quantities dependent on R are to be evaluated at R =
Ro. We choose Ro to be the radius of the
circular orbit described by the guiding centre of the final
orbit. Further we assume
that  is small and that we
are close to a resonance, i.e.
(
is small and that we
are close to a resonance, i.e.
( 2 -
2 -
 m2) is
small. We then get the solution to
Eqs. (2) and (3) after oscillations
around the central orbit have damped out due to friction:
m2) is
small. We then get the solution to
Eqs. (2) and (3) after oscillations
around the central orbit have damped out due to friction:
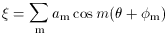
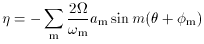
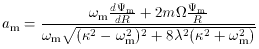
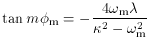
 is
small, the amplitudes get large for
is
small, the amplitudes get large for
 m
m

 ,
and the terms with the corresponding value of m will dominate the
solutions. The equations describe an orbit closed in a frame rotating
with the perturbing potential and an orientation with respect to the
bar determined by the phase angle
,
and the terms with the corresponding value of m will dominate the
solutions. The equations describe an orbit closed in a frame rotating
with the perturbing potential and an orientation with respect to the
bar determined by the phase angle
 m. Realising from
Eq. (1) that
m. Realising from
Eq. (1) that