


With the help of some simple stellar population synthesis tools it is
possible at this stage to make an estimate of the integrated stellar mass
density today. The total bolometric luminosity of a simple stellar
population (a single generation of coeval stars) having mass M
can be well approximated by a power-law with time for all ages t
 100
Myr,
100
Myr,
(cf. [5]),
where we have assumed solar metallicity and a Salpeter IMF truncated at 0.1
and 125 M
The total background light observed at Earth (t =
tH) is
where the factor (1 + z) at the denominator is lost to cosmic expansion
when converting from observed to radiated luminosity density. From the
above equations it is easy to derive
The observations shown in Figure 1
therefore imply a ``fiducial'' mean star
formation density of <
(corresponding to 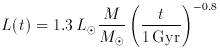
 . In
a stellar system with arbitrary star-formation rate per
unit cosmological volume,
. In
a stellar system with arbitrary star-formation rate per
unit cosmological volume,  *, the comoving bolometric emissivity
at time t is given by the convolution integral
*, the comoving bolometric emissivity
at time t is given by the convolution integral
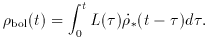
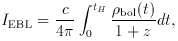
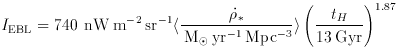 (4)
(4)
 > = 0.054 I40 M
> = 0.054 I40 M yr-1 Mpc-3.
In the instantaneous recycling approximation, the total stellar mass
density observed today is
yr-1 Mpc-3.
In the instantaneous recycling approximation, the total stellar mass
density observed today is
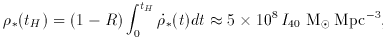 (5)
(5)
 * = 0.007
I40) where R is the mass fraction
of a generation of stars that is returned to the interstellar medium,
R
* = 0.007
I40) where R is the mass fraction
of a generation of stars that is returned to the interstellar medium,
R  0.3 for a Salpeter
IMF. The optical /COBE background
therefore requires that about 10% of the nucleosynthetic baryons (
0.3 for a Salpeter
IMF. The optical /COBE background
therefore requires that about 10% of the nucleosynthetic baryons ( b
h50 = 0.08
[4])
are in the forms of stars and their remnants.
The predicted stellar mass-to-blue light ratio is
< M / LB >
b
h50 = 0.08
[4])
are in the forms of stars and their remnants.
The predicted stellar mass-to-blue light ratio is
< M / LB >  5.
Note that these values are quite sensitive to the
lower-mass cutoff of the IMF, as very-low mass stars can contribute
significantly to the mass but not to the integrated light of the whole stellar
population. A lower cutoff of 0.5 M
5.
Note that these values are quite sensitive to the
lower-mass cutoff of the IMF, as very-low mass stars can contribute
significantly to the mass but not to the integrated light of the whole stellar
population. A lower cutoff of 0.5 M instead of the 0.1
M
instead of the 0.1
M adopted
would decrease the mass-to-light ratio (and
adopted
would decrease the mass-to-light ratio (and  *) by a factor of 1.9
for a Salpeter function.
*) by a factor of 1.9
for a Salpeter function.