


The Jeans length  J was
originally defined
(Jeans 1928)
in Newtonian gravity as the critical wavelength that separates
oscillatory and exponentially-growing density perturbations in an
infinite, uniform, and stationary distribution of gas. On scales
J was
originally defined
(Jeans 1928)
in Newtonian gravity as the critical wavelength that separates
oscillatory and exponentially-growing density perturbations in an
infinite, uniform, and stationary distribution of gas. On scales
 smaller than
smaller than
 J, the sound
crossing time,
J, the sound
crossing time,  /
cs is shorter than the gravitational free-fall time,
(G
/
cs is shorter than the gravitational free-fall time,
(G )-1/2,
allowing the build-up of a pressure force that counteracts gravity. On
larger scales, the pressure gradient force is too slow to react to a
build-up of the attractive gravitational force. The Jeans mass is
defined as the mass within a sphere of radius
)-1/2,
allowing the build-up of a pressure force that counteracts gravity. On
larger scales, the pressure gradient force is too slow to react to a
build-up of the attractive gravitational force. The Jeans mass is
defined as the mass within a sphere of radius
 J / 2,
MJ = (4
J / 2,
MJ = (4 / 3)
/ 3)
 (
( J /
2)3. In a perturbation with a mass
greater than MJ, the self-gravity cannot be supported by the
pressure gradient, and so the gas is unstable to gravitational
collapse. The Newtonian derivation of the Jeans instability suffers
from a conceptual inconsistency, as the unperturbed gravitational
force of the uniform background must induce bulk motions (compare
Binney & Tremaine
1987).
However, this inconsistency is remedied
when the analysis is done in an expanding universe.
J /
2)3. In a perturbation with a mass
greater than MJ, the self-gravity cannot be supported by the
pressure gradient, and so the gas is unstable to gravitational
collapse. The Newtonian derivation of the Jeans instability suffers
from a conceptual inconsistency, as the unperturbed gravitational
force of the uniform background must induce bulk motions (compare
Binney & Tremaine
1987).
However, this inconsistency is remedied
when the analysis is done in an expanding universe.
The perturbative derivation of the Jeans instability criterion can be
carried out in a cosmological setting by considering a sinusoidal
perturbation superposed on a uniformly expanding background. Here, as
in the Newtonian limit, there is a critical wavelength
 J that
separates oscillatory and growing modes. Although the expansion of
the background slows down the exponential growth of the amplitude to a
power-law growth, the fundamental concept of a minimum mass that can
collapse at any given time remains the same (see, e.g.
Kolb & Turner 1990;
Peebles 1993).
J that
separates oscillatory and growing modes. Although the expansion of
the background slows down the exponential growth of the amplitude to a
power-law growth, the fundamental concept of a minimum mass that can
collapse at any given time remains the same (see, e.g.
Kolb & Turner 1990;
Peebles 1993).
We consider a mixture of dark matter and baryons with density parameters
 dmz =
dmz =
 dm
/
dm
/  c
and
c
and  bz =
bz =
 b /
b /
 c, where
c, where
 dm
is the average dark matter density,
dm
is the average dark matter density,
 b
is the average baryonic density,
b
is the average baryonic density,
 c
is the critical density, and
c
is the critical density, and
 dmz +
dmz +
 bz =
bz =
 mz is
given by equation (23). We also assume
spatial fluctuations in the gas and dark matter densities with the
form of a single spherical Fourier mode on a scale much smaller than
the horizon,
mz is
given by equation (23). We also assume
spatial fluctuations in the gas and dark matter densities with the
form of a single spherical Fourier mode on a scale much smaller than
the horizon,
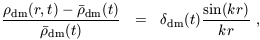
| (33) |
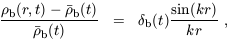
| (34) |
where  dm(t) and
dm(t) and
 b(t) are the
background densities of the dark matter and baryons,
b(t) are the
background densities of the dark matter and baryons,
 dm(t) and
dm(t) and
 b(t) are
the dark matter and baryon
overdensity amplitudes, r is the comoving radial coordinate, and
k is the comoving perturbation wavenumber. We adopt an ideal gas
equation-of-state for the baryons with a specific heat ratio
b(t) are
the dark matter and baryon
overdensity amplitudes, r is the comoving radial coordinate, and
k is the comoving perturbation wavenumber. We adopt an ideal gas
equation-of-state for the baryons with a specific heat ratio
 =
5/3. Initially, at time t = ti, the gas
temperature is uniform
Tb(r, ti) =
Ti, and the perturbation amplitudes are small
=
5/3. Initially, at time t = ti, the gas
temperature is uniform
Tb(r, ti) =
Ti, and the perturbation amplitudes are small
 dm,i,
dm,i,
 b,i << 1. We
define the region inside the first zero of
sin(kr) / (kr), namely 0 < kr <
b,i << 1. We
define the region inside the first zero of
sin(kr) / (kr), namely 0 < kr <
 , as the collapsing ``object''.
, as the collapsing ``object''.
The evolution of the temperature of the baryons
Tb(r, t) in
the linear regime is determined by the coupling of their free
electrons to the Cosmic Microwave Background (CMB) through Compton
scattering, and by the adiabatic expansion of the gas. Hence,
Tb(r, t) is generally somewhere between
the CMB temperature,
T
 (1 +
z)-1 and the adiabatically-scaled
temperature Tad
(1 +
z)-1 and the adiabatically-scaled
temperature Tad
 (1 +
z)-2. In the limit of tight coupling to
T
(1 +
z)-2. In the limit of tight coupling to
T ,
the gas temperature remains uniform. On the
other hand, in the adiabatic limit, the temperature develops a
gradient according to the relation
,
the gas temperature remains uniform. On the
other hand, in the adiabatic limit, the temperature develops a
gradient according to the relation
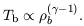
| (35) |
The evolution of dark matter overdensity,
 dm(t), in the
linear regime is described by the equation (see Section 9.3.2 of
Kolb & Turner 1990),
dm(t), in the
linear regime is described by the equation (see Section 9.3.2 of
Kolb & Turner 1990),
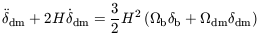
| (36) |
whereas the evolution of the overdensity of the baryons,
 b(t), is
described by
b(t), is
described by
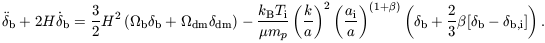
| (37) |
Here, H(t) =  /
a is the Hubble parameter at a cosmological time
t, and µ = 1.22 is the mean molecular weight of the neutral
primordial gas in atomic units. The parameter
/
a is the Hubble parameter at a cosmological time
t, and µ = 1.22 is the mean molecular weight of the neutral
primordial gas in atomic units. The parameter
 distinguishes
between the two limits for the evolution of the gas temperature. In
the adiabatic limit
distinguishes
between the two limits for the evolution of the gas temperature. In
the adiabatic limit  = 1, and when the baryon temperature is
uniform and locked to the background radiation,
= 1, and when the baryon temperature is
uniform and locked to the background radiation,
 = 0. The last
term on the right hand side (in square brackets) takes into account
the extra pressure gradient force in
= 0. The last
term on the right hand side (in square brackets) takes into account
the extra pressure gradient force in
 (
( bT) =
(T
bT) =
(T 
 b +
b +
 b
b
 T), arising from the
temperature
gradient which develops in the adiabatic limit. The Jeans wavelength
T), arising from the
temperature
gradient which develops in the adiabatic limit. The Jeans wavelength
 J =
2
J =
2 / kJ is
obtained by setting the right-hand side of
equation (37) to zero, and solving for the critical wavenumber
kJ. As can be seen from equation (37), the critical
wavelength
/ kJ is
obtained by setting the right-hand side of
equation (37) to zero, and solving for the critical wavenumber
kJ. As can be seen from equation (37), the critical
wavelength  J (and
therefore the mass MJ) is in general
time-dependent. We infer from equation (37) that as time
proceeds, perturbations with increasingly smaller initial wavelengths
stop oscillating and start to grow.
J (and
therefore the mass MJ) is in general
time-dependent. We infer from equation (37) that as time
proceeds, perturbations with increasingly smaller initial wavelengths
stop oscillating and start to grow.
To estimate the Jeans wavelength, we equate the right-hand-side of
equation (37) to zero. We further approximate
 b ~
b ~
 dm, and consider
sufficiently high redshifts at which
the universe is matter-dominated and flat (equations (9)
and (10) in
Section 2.1). We also assume
dm, and consider
sufficiently high redshifts at which
the universe is matter-dominated and flat (equations (9)
and (10) in
Section 2.1). We also assume
 b <<
b <<
 m, where
m, where
 m =
m =
 dm +
dm +
 b is the total
matter density parameter. Following cosmological recombination at
z
b is the total
matter density parameter. Following cosmological recombination at
z  103,
the residual ionization of the cosmic gas keeps its
temperature locked to the CMB temperature (via Compton scattering)
down to a redshift of (p. 179 of
Peebles 1993)
103,
the residual ionization of the cosmic gas keeps its
temperature locked to the CMB temperature (via Compton scattering)
down to a redshift of (p. 179 of
Peebles 1993)
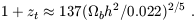
| (38) |
In the redshift range between recombination and zt,
 = 0 and
= 0 and
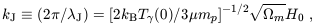
| (39) |
so that the Jeans mass is therefore redshift independent and obtains the value (for the total mass of baryons and dark matter)
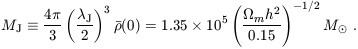
| (40) |
Based on the similarity of MJ to the mass of a globular cluster, Peebles & Dicke (1968) suggested that globular clusters form as the first generation of baryonic objects shortly after cosmological recombination. Peebles & Dicke assumed a baryonic universe, with a nonlinear fluctuation amplitude on small scales at z ~ 103, a model which has by now been ruled out. The lack of a dominant mass of dark matter inside globular clusters (Moore 1996; Heggie & Hut 1996) makes it unlikely that they formed through direct cosmological collapse, and more likely that they resulted from fragmentation during the process of galaxy formation. Furthermore, globular clusters have been observed to form in galaxy mergers (e.g., Miller et al. 1997).
At z  zt, the gas temperature declines adiabatically as
[(1 + z) / (1 + zt)]2 (i.e.,
zt, the gas temperature declines adiabatically as
[(1 + z) / (1 + zt)]2 (i.e.,
 = 1) and the
total Jeans mass obtains the value,
= 1) and the
total Jeans mass obtains the value,
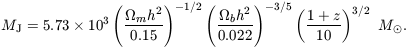
| (41) |
Note that we have neglected Compton drag, i.e., the radiation force which suppresses gravitational growth of structure in the baryon fluid as long as the electron abundance is sufficiently high to keep the baryons dynamically coupled to the photons. After cosmological recombination, the net friction force on the predominantly neutral fluid decreases dramatically, allowing the baryons to fall into dark matter potential wells, and essentially erasing the memory of Compton drag by z ~ 100 (e.g., Section 5.3.1. of Hu 1995).
It is not clear how the value of the Jeans mass derived above relates
to the mass of collapsed, bound objects. The above analysis is
perturbative (Eqs. [36] and [37] are valid only as long as
 b and
b and
 dm are much
smaller than unity),
and thus can only describe the initial phase of the collapse. As
dm are much
smaller than unity),
and thus can only describe the initial phase of the collapse. As
 b and
b and
 dm grow and
become larger than
unity, the density profiles start to evolve and dark matter shells may
cross baryonic shells
(Haiman, Thoul, &
Loeb 1996)
due to their different dynamics. Hence the amount of mass enclosed
within a given baryonic shell may increase with time, until eventually the dark
matter pulls the baryons with it and causes their collapse even
for objects below the Jeans mass.
dm grow and
become larger than
unity, the density profiles start to evolve and dark matter shells may
cross baryonic shells
(Haiman, Thoul, &
Loeb 1996)
due to their different dynamics. Hence the amount of mass enclosed
within a given baryonic shell may increase with time, until eventually the dark
matter pulls the baryons with it and causes their collapse even
for objects below the Jeans mass.
Even within linear theory, the Jeans mass is related only to the
evolution of perturbations at a given time. When the Jeans mass itself
varies with time, the overall suppression of the growth of
perturbations depends on a time-averaged Jeans mass.
Gnedin & Hui (1998)
showed that the correct time-averaged mass is the filtering
mass MF = (4 / 3)
/ 3)
 (2
(2 a
/ kF)3, in terms of the
comoving wavenumber kF associated with the ``filtering
scale''. The
wavenumber kF is related to the Jeans wavenumber
kJ by
a
/ kF)3, in terms of the
comoving wavenumber kF associated with the ``filtering
scale''. The
wavenumber kF is related to the Jeans wavenumber
kJ by
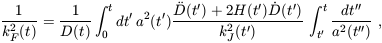
| (42) |
where D(t) is the linear growth
factor (Section 2.2). At high redshift
(where  mz ->
1), this relation simplifies to
(Gnedin 2000b)
mz ->
1), this relation simplifies to
(Gnedin 2000b)
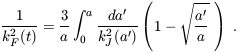
| (43) |
Then the relationship between the
linear overdensity of the dark matter
 dm and the linear
overdensity of the baryons
dm and the linear
overdensity of the baryons
 b, in the limit
of small k, can be written as
(Gnedin & Hui 1998)
b, in the limit
of small k, can be written as
(Gnedin & Hui 1998)
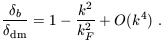
| (44) |
Linear theory specifies whether an initial perturbation, characterized
by the parameters k,
 dm,i,
dm,i,
 b,i and
ti, begins to grow. To determine the minimum mass of
nonlinear baryonic objects resulting from the shell-crossing and
virialization of the dark matter, we must use a different model which
examines the response of the gas to the gravitational potential of a
virialized dark matter halo.
b,i and
ti, begins to grow. To determine the minimum mass of
nonlinear baryonic objects resulting from the shell-crossing and
virialization of the dark matter, we must use a different model which
examines the response of the gas to the gravitational potential of a
virialized dark matter halo.
3.2. Response of Baryons to Nonlinear Dark Matter Potentials
The dark matter is assumed to be cold and to dominate gravity, and so its collapse and virialization proceeds unimpeded by pressure effects. In order to estimate the minimum mass of baryonic objects, we must go beyond linear perturbation theory and examine the baryonic mass that can accrete into the final gravitational potential well of the dark matter.
For this purpose, we assume that the dark matter had already
virialized and produced a gravitational potential
 (r) at a
redshift zvir (with
(r) at a
redshift zvir (with
 -> 0 at large distances,
and
-> 0 at large distances,
and  < 0 inside the object)
and calculate the resulting
overdensity in the gas distribution, ignoring cooling (an assumption
justified by spherical collapse simulations which indicate that
cooling becomes important only after virialization; see
Haiman, Thoul, &
Loeb 1996).
< 0 inside the object)
and calculate the resulting
overdensity in the gas distribution, ignoring cooling (an assumption
justified by spherical collapse simulations which indicate that
cooling becomes important only after virialization; see
Haiman, Thoul, &
Loeb 1996).
After the gas settles into the dark matter potential well, it satisfies the hydrostatic equilibrium equation,
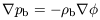
| (45) |
where pb and
 b are
the pressure and mass density of the gas. At z
b are
the pressure and mass density of the gas. At z
 100 the gas
temperature is decoupled from the CMB, and its pressure evolves
adiabatically (ignoring atomic or molecular cooling),
100 the gas
temperature is decoupled from the CMB, and its pressure evolves
adiabatically (ignoring atomic or molecular cooling),
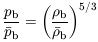
| (46) |
where a bar denotes the background conditions. We substitute equation (46) into (45) and get the solution,
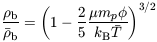
| (47) |
where 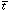 =
=
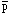 b
µmp / (kB
b
µmp / (kB
 b)
is the background gas temperature. If we define
Tvir = - 1/3 µmp
b)
is the background gas temperature. If we define
Tvir = - 1/3 µmp
 / kB as the
virial temperature for a potential
depth -
/ kB as the
virial temperature for a potential
depth -  , then the overdensity
of the baryons at the virialization redshift is
, then the overdensity
of the baryons at the virialization redshift is
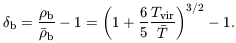
| (48) |
This solution is approximate for two reasons: (i) we assumed that the gas is stationary throughout the entire region and ignored the transitions to infall and the Hubble expansion at the interface between the collapsed object and the background intergalactic medium (henceforth IGM), and (ii) we ignored entropy production at the virialization shock surrounding the object. Nevertheless, the result should provide a better estimate for the minimum mass of collapsed baryonic objects than the Jeans mass does, since it incorporates the nonlinear potential of the dark matter.
We may define the threshold for the collapse of baryons by the
criterion that their mean overdensity,
 b, exceeds a
value of 100, amounting to
b, exceeds a
value of 100, amounting to
 50% of the baryons
that would
assemble in the absence of gas pressure, according to the spherical
top-hat collapse model (Section 2.3).
Equation (48) then implies that
Tvir > 17.2
50% of the baryons
that would
assemble in the absence of gas pressure, according to the spherical
top-hat collapse model (Section 2.3).
Equation (48) then implies that
Tvir > 17.2
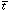 .
.
As mentioned before, the gas temperature evolves at z
 160
according to the relation
160
according to the relation
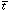
 170[(1 + z) /
100]2 K. This implies that baryons are overdense by
170[(1 + z) /
100]2 K. This implies that baryons are overdense by
 b > 100 only
inside halos with a virial temperature Tvir
b > 100 only
inside halos with a virial temperature Tvir
 2.9 ×
103 [(1 + z)/100]2
K. Based on the top-hat model
(Section 2.3), this implies a minimum halo
mass for baryonic objects of
2.9 ×
103 [(1 + z)/100]2
K. Based on the top-hat model
(Section 2.3), this implies a minimum halo
mass for baryonic objects of
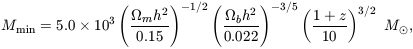
| (49) |
where we set µ = 1.22 and consider sufficiently high redshifts so
that  mz
mz
 1. This minimum mass is
coincidentally almost
identical to the naive Jeans mass calculation of linear theory in
equation (41) despite the fact that it incorporates shell
crossing by the dark matter, which is not accounted for by linear
theory. Unlike the Jeans mass, the minimum mass depends on the choice
for an overdensity threshold [taken arbitrarily as
1. This minimum mass is
coincidentally almost
identical to the naive Jeans mass calculation of linear theory in
equation (41) despite the fact that it incorporates shell
crossing by the dark matter, which is not accounted for by linear
theory. Unlike the Jeans mass, the minimum mass depends on the choice
for an overdensity threshold [taken arbitrarily as
 b > 100 in
equation (49)]. To estimate the minimum halo
mass which produces any significant accretion we set, e.g.,
b > 100 in
equation (49)]. To estimate the minimum halo
mass which produces any significant accretion we set, e.g.,
 b = 5, and get a
mass which is lower than Mmin by a factor of 27.
b = 5, and get a
mass which is lower than Mmin by a factor of 27.
Of course, once the first stars and quasars form they heat the surrounding IGM by either outflows or radiation. As a result, the Jeans mass which is relevant for the formation of new objects changes (Ostriker & Gnedin 1996; Gnedin 2000a). The most dramatic change occurs when the IGM is photo-ionized and is consequently heated to a temperature of ~ (1-2) × 104 K. As we discuss in Section 6.5, this heating episode had a dramatic impact on galaxy formation.
3.3. Molecular Chemistry, Photo-Dissociation, and Cooling
Before metals are produced, the primary molecule which acquires sufficient abundance to affect the thermal state of the pristine cosmic gas is molecular hydrogen, H2. The dominant H2 formation process is
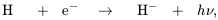
| (50) |
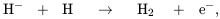
| (51) |
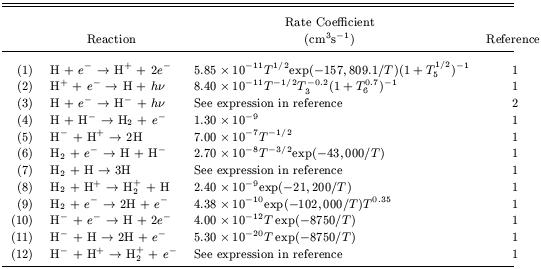
where free electrons act as catalysts. The complete set of chemical reactions leading to the formation of H2 is summarized in Table 1, together with the associated rate coefficients (see also Haiman, Thoul, & Loeb 1996; Abel et al. 1997; Galli & Palla 1998; and the review by Abel & Haiman 2000). Table 2 shows the same for deuterium mediated reactions. Due to the low gas density, the chemical reactions are slow and the molecular abundance is far from its value in chemical equilibrium. After cosmological recombination the fractional H2 abundance is small, ~ 10-6 relative to hydrogen by number (Lepp & Shull 1984; Shapiro, Giroux & Babul 1994). At redshifts z << 100, the gas temperature in most regions is too low for collisional ionization to be effective, and free electrons (over and above the residual electron fraction) are mostly produced through photoionization of neutral hydrogen by UV or X-ray radiation.
|
| References. - (1) Haiman, Thoul, & Loeb 1996; (2) Abel, et al. 1997. |

|
| References. - (1) Haiman, Thoul, & Loeb 1996; (3) Gali & Palla 1998. |
In objects with baryonic masses
 3 × 104
M
3 × 104
M , gravity
dominates and results in the bottom-up hierarchy of structure
formation characteristic of CDM cosmologies; at lower masses, gas
pressure delays the collapse. The first objects to collapse are those
at the mass scale that separates these two regimes. Such objects
reach virial temperatures of several hundred degrees and can fragment
into stars only through cooling by molecular hydrogen (e.g.,
Abel 1995;
Tegmark et al. 1997).
In other words, there are two independent
minimum mass thresholds for star formation: the Jeans mass (related to
accretion) and the cooling mass. For the very first objects, the
cooling threshold is somewhat higher and sets a lower limit on the
halo mass of ~ 5 × 104
M
, gravity
dominates and results in the bottom-up hierarchy of structure
formation characteristic of CDM cosmologies; at lower masses, gas
pressure delays the collapse. The first objects to collapse are those
at the mass scale that separates these two regimes. Such objects
reach virial temperatures of several hundred degrees and can fragment
into stars only through cooling by molecular hydrogen (e.g.,
Abel 1995;
Tegmark et al. 1997).
In other words, there are two independent
minimum mass thresholds for star formation: the Jeans mass (related to
accretion) and the cooling mass. For the very first objects, the
cooling threshold is somewhat higher and sets a lower limit on the
halo mass of ~ 5 × 104
M at z ~ 20.
at z ~ 20.
However, molecular hydrogen (H2) is fragile and can easily be
photo-dissociated by photons with energies of 11.26-13.6eV, to
which the IGM is transparent even before it is ionized. The
photo-dissociation occurs through a two-step process, first suggested by
Solomon in 1965
(compare
Field et al. 1966)
and later analyzed quantitatively by
Stecher & Williams (1967).
Haiman, Rees, & Loeb
(1997)
evaluated the average cross-section for this process between
11.26eV and 13.6eV, by summing the oscillator strengths for the Lyman
and Werner bands of H2, and obtained a value of
3.71 × 10-18 cm2. They showed that the
UV flux capable of
dissociating H2 throughout the collapsed environments in the
universe is lower by more than two orders of magnitude than the
minimum flux necessary to ionize the universe. The inevitable
conclusion is that soon after trace amounts of stars form, the
formation of additional stars due to H2 cooling is
suppressed. Further fragmentation is possible only through atomic
line cooling, which is effective in objects with much higher virial
temperatures, Tvir
 104K. Such objects correspond to a total mass
104K. Such objects correspond to a total mass
 108
M
108
M [(1 +
z) / 10]-3/2.
Figure 4
illustrates this sequence of events by describing two classes of
objects: those with Tvir < 104K (small
dots) and those with
Tvir > 104K (large dots). In the first
stage (top panel),
some low-mass objects collapse, form stars, and create ionized
hydrogen (H II) bubbles around them. Once the UV background
between 11.2-13.6eV reaches a specific critical level, H2 is
photo-dissociated throughout the universe and the formation of new
stars is delayed until objects with
Tvir
[(1 +
z) / 10]-3/2.
Figure 4
illustrates this sequence of events by describing two classes of
objects: those with Tvir < 104K (small
dots) and those with
Tvir > 104K (large dots). In the first
stage (top panel),
some low-mass objects collapse, form stars, and create ionized
hydrogen (H II) bubbles around them. Once the UV background
between 11.2-13.6eV reaches a specific critical level, H2 is
photo-dissociated throughout the universe and the formation of new
stars is delayed until objects with
Tvir  104K collapse
(Haiman, Abel, &
Rees 2000;
Ciardi, Ferrara, &
Abel 2000;
Ciardi et al. 2000).
Machacek, Bryan &
Abel (2000)
have confirmed that the
soft UV background can delay the cooling and collapse of low-mass
halos (~ 106
M
104K collapse
(Haiman, Abel, &
Rees 2000;
Ciardi, Ferrara, &
Abel 2000;
Ciardi et al. 2000).
Machacek, Bryan &
Abel (2000)
have confirmed that the
soft UV background can delay the cooling and collapse of low-mass
halos (~ 106
M ) based on
analytical arguments and
three-dimensional hydrodynamic simulations; they also determined the
halo mass threshold for collapse for a range of UV fluxes.
Nishi & Omukai
(1999;
see also
Silk 1977)
have argued that the
photo-dissociation of H2 could be even more effective due to a
small number of stars embedded within the gas clouds themselves.
) based on
analytical arguments and
three-dimensional hydrodynamic simulations; they also determined the
halo mass threshold for collapse for a range of UV fluxes.
Nishi & Omukai
(1999;
see also
Silk 1977)
have argued that the
photo-dissociation of H2 could be even more effective due to a
small number of stars embedded within the gas clouds themselves.
When considering the photo-dissociation of H2 before reionization,
it is important to incorporate the processed spectrum of the UV
background at photon energies below the Lyman limit. Due to the
absorption at the Lyman-series resonances this spectrum obtains the
sawtooth shape shown in Figure 11. For any
photon energy
above Ly at a particular
redshift, there is a limited redshift
interval beyond which no contribution from sources is possible because
the corresponding photons are absorbed through one of the Lyman-series
resonances along the way. Consider, for example, an energy of 11 eV at
an observed redshift z = 10. Photons received at this energy would
have to be emitted at the 12.1 eV
Ly
at a particular
redshift, there is a limited redshift
interval beyond which no contribution from sources is possible because
the corresponding photons are absorbed through one of the Lyman-series
resonances along the way. Consider, for example, an energy of 11 eV at
an observed redshift z = 10. Photons received at this energy would
have to be emitted at the 12.1 eV
Ly line from
z = 11.1. Thus,
sources in the redshift interval 10-11.1 could be seen at 11 eV, but
radiation emitted by sources at z > 11.1 eV would have passed through
the 12.1 eV energy at some intermediate redshift, and would have been
absorbed. Thus, an observer viewing the universe at any photon energy
above Ly
line from
z = 11.1. Thus,
sources in the redshift interval 10-11.1 could be seen at 11 eV, but
radiation emitted by sources at z > 11.1 eV would have passed through
the 12.1 eV energy at some intermediate redshift, and would have been
absorbed. Thus, an observer viewing the universe at any photon energy
above Ly would see sources
only out to some horizon, and the
size of that horizon would depend on the photon energy. The number of
contributing sources, and hence the total background flux at each
photon energy, would depend on how far this energy is from the nearest
Lyman resonance. Most of the photons absorbed along the way would be
re-emitted at Ly
would see sources
only out to some horizon, and the
size of that horizon would depend on the photon energy. The number of
contributing sources, and hence the total background flux at each
photon energy, would depend on how far this energy is from the nearest
Lyman resonance. Most of the photons absorbed along the way would be
re-emitted at Ly and then
redshifted to lower energies. The
result is a sawtooth spectrum for the UV background before
reionization, with an enhancement below the
Ly
and then
redshifted to lower energies. The
result is a sawtooth spectrum for the UV background before
reionization, with an enhancement below the
Ly energy (see
Haiman et al. 1997
for more details). Unfortunately, the direct
detection of the redshifted sawtooth spectrum as a remnant of the
reionization epoch is not feasible due to the much higher flux
contributed by foreground sources at later cosmic times.
energy (see
Haiman et al. 1997
for more details). Unfortunately, the direct
detection of the redshifted sawtooth spectrum as a remnant of the
reionization epoch is not feasible due to the much higher flux
contributed by foreground sources at later cosmic times.
The radiative feedback on H2 need not be only
negative, however. In the dense interiors of gas clouds, the
formation rate of H2 could be accelerated through the production of
free electrons by X-rays. This effect could counteract the
destructive role of H2 photo-dissociation
(Haiman, Rees, &
Loeb 1996).
Haiman, Abel, & Rees
(2000)
have shown that if a significant
(  10%) fraction of
the early UV background is produced by
massive black holes (mini-quasars) with hard spectra extending to
photon energies ~ 1 keV, then the X-rays will catalyze
H2 production and the net radiative feedback will be positive,
allowing low mass objects to fragment into stars. These objects may
greatly alter the topology of reionization
(Section 6.3). However,
if such quasars do not exist or if low mass objects are disrupted by
supernova-driven winds (see Section 7.2),
then most of the stars
will form inside objects with virial temperatures
10%) fraction of
the early UV background is produced by
massive black holes (mini-quasars) with hard spectra extending to
photon energies ~ 1 keV, then the X-rays will catalyze
H2 production and the net radiative feedback will be positive,
allowing low mass objects to fragment into stars. These objects may
greatly alter the topology of reionization
(Section 6.3). However,
if such quasars do not exist or if low mass objects are disrupted by
supernova-driven winds (see Section 7.2),
then most of the stars
will form inside objects with virial temperatures
 104K, where
atomic cooling dominates. Figure 12 and
Table 3 summarize
the cooling rates as a function of gas temperature in high-redshift,
metal-free objects.
104K, where
atomic cooling dominates. Figure 12 and
Table 3 summarize
the cooling rates as a function of gas temperature in high-redshift,
metal-free objects.
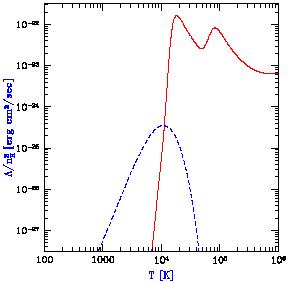
|
Figure 12.
Cooling rates as a function of temperature for a primordial
gas composed of atomic hydrogen and helium, as well as molecular
hydrogen, in the absence of any external radiation. We assume a
hydrogen number density
nH = 0.045 cm-3, corresponding to
the mean density of virialized halos at z = 10. The plotted quantity
|

|
| Note. - T is the gas temperature in K, T3 = T / 103 K, T5 = T / 105 K, T6 = T / 106 K, ne is the density of free electrons, z is the redshift, and TCMB = 2.73 (1 + z) K is the temperature of the CMB. |
| References. - (1) Galli & Palla 1998; (2) Flower, Le Bourlot, Pineau des Forêts, & Roueff 2000; (3) Cen 1992; Verner & Ferland 1996; Ferland et al. 1992; Voronov 1997 (4) Ikeuchi & Ostriker 1986. |