5. GALAXY PROPERTIES

5.1. Formation and Properties of Galactic Disks

The formation of disk galaxies within hierarchical models of structure formation was first explored by Fall & Efstathiou (1980). More recently, the distribution of disk sizes was derived and compared to observations by Dalcanton, Spergel, & Summers (1997) and Mo, Mao, & White (1998). Although these authors considered a number of detailed models, we adopt here the simple model of an exponential disk in a singular isothermal sphere halo. We consider a halo of mass M, virial radius r_vir, total energy E, and angular momentum J, for which the spin parameter is defined as

(55)

The spin parameter simply expresses the halo angular momentum in a dimensionless form. The gas disk is assumed to collapse to a state of rotational support in the dark matter halo. If the disk mass is a fraction m_d of the halo mass and its angular momentum is a fraction j_d of that of the halo, then the exponential scale radius of the disk is given by (Mo et al. 1998)

(56)

The observed distribution of disk sizes suggests that the specific angular momentum of the disk is similar to that of the halo (e.g., Dalcanton et al. 1997; Mo et al. 1998), and so we assume that j_d/m_d = 1. Although this result is implied by observed galactic disks, its origin in the disk formation process is still unclear. The formation of galactic disks has been investigated in a large number of numerical simulations (Navarro & Benz 1991; Evrard, Summers, & Davis 1994; Navarro, Frenk, & White 1995; Tissera, Lambas, & Abadi 1997; Navarro & Steinmetz 1997; Elizondo, et al. 1999). The overall conclusion is that the collapsing gas loses angular momentum to the dark matter halo during mergers, and the disks which form are much smaller than observed galactic disks. The most widely discussed solution for this problem is to prevent the gas from collapsing into a disk by injecting energy through supernova feedback (e.g. Eke, Efstathiou, & Wright 1999; Binney, Gerhard, & Silk 2001; Efstathiou 2000). However, some numerical simulations suggest that feedback may not adequately suppress the angular momentum losses (Navarro & Steinmetz 2000).

With the assumption that j_d / m_d = 1, the distribution of disk sizes is then determined by the Press-Schechter halo abundance and by the distribution of spin parameters [along with equation (24) for r_vir]. The spin parameter distribution is approximately independent of mass, environment, and cosmological parameters, apparently a consequence of the scale-free properties of the early tidal torques between neighboring systems responsible for the spin of individual halos (Peebles 1969; White 1984; Barnes & Efstathiou 1987; Heavens & Peacock 1988; Steinmetz & Bartelmann 1995; Eisenstein & Loeb 1995a; Cole & Lacey 1996; Catelan & Theuns 1996). This distribution approximately follows a lognormal distribution in the vicinity of the peak,

(57)

with 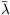= 0.05 and = 0.5 following Mo et al. (1998), who determined these values based on the N-body simulations of Warren et al. (1992). Although Mo et al. (1998) suggest a lower cutoff on due to disk instability, it is unclear if halos with low indeed cannot contain disks. If a dense bulge exists, it can prevent bar instabilities, or if a bar forms it may be weakened or destroyed when a bulge subsequently forms (Sellwood & Moore 1999).

5.2. Phenomenological Prescription for Star Formation

Schmidt (1959) put forth the hypothesis that the rate of star formation in a given region varies as a power of the gas density within that region. Thus, the star formation rate can be parameterized as

(58)

where _* is the mass density of stars, and _g is the mass density of gas. Although Schmidt originally focused on different regions within our own Galaxy, this relation has since been used to interpret observations of the global star formation rates in different galaxies.

One particular value of N is theoretically favored for self-gravitating disks (e.g., Larson 1992; Elmegreen 1994). The star formation rate can be written in the form

(59)

where is an efficiency coefficient, and t_c is a characteristic time for star formation. If t_c is proportional to the dynamical free-fall time, i.e., t_{c g}^-1/2, then N = 1.5. However, observations yield estimates of surface densities , not volume densities . If the average gas scale height is roughly constant in different environments, then the same relation as equation (58) should hold between the surface densities of stars and gas, with N = 1.5.

Such a relation has, indeed, been observed to hold over a large range of physical conditions in galaxies. Synthetic models which include stellar evolution tracks and stellar atmosphere models are used to infer star formation rates using spectral observations of stellar populations. Star formation rates have been inferred in this way in the disks of normal spiral and irregular galaxies, most often using H luminosities. Star formation also occurs in much denser environments in the nuclear regions of galaxies, where far-infrared luminosities are most useful for determining star formation rates. Thus, the relation between star formation and gas density has been measured over conditions ranging from the outskirts of normal disks to the central engines of infrared-luminous starburst galaxies. The result is a tight correlation in accordance with the Schmidt law, empirically given by (Kennicutt 1998)

(60)

where _SFR and _gas are the disk-averaged star formation rate and gas surface densities, respectively. This relation is observed to hold over almost five orders of magnitude in gas surface density.