Growth of primordial fluctuations

4.2.1 Growth of primordial fluctuations

Suppose we start our analysis shortly after Annihilation. Then, a primordial energy density fluctuation spectrum must be assumed. One of the most simple hypotheses is the spectrum of Harrison and Zeldovich which is rest mass independent and which arises naturally from the quantum fluctuation at Inflation, but there are other more exotic possibilities; indeed, the spectrum has been characterized by some parameters which are considered free in some numerical calculations. The subsequent evolution is a consequence of this initial spectrum and of the nature of the matter, mainly through the equation of state.

Most models do not explicitly consider this first phase. It is considered that an unknown primordial density fluctuation spectrum is responsible for an unknown post-Recombination spectrum and this, therefore, is equivalent to assuming the initial spectrum after Recombination and this complicated phase is thus avoided. We consider this procedure somewhat dangerous because even if the initial spectrum is random some regular structure may be inherited after Recombination. For example, primordial magnetic fields may be responsible for very large scale filaments ( $\sim$ 100 Mpc) as discussed later. Moreover, the existence of periodic structures forming a lattice, actually observed whatever the cause may be, must be understood to assess how CDM halos merge at later epochs. These points will be addressed later.

As in the case of stellar collapses, the basic concept is Jeans' Mass. We must know which masses are able to collapse and how the collapse grows as a function of time. Both phenomena depend on the epoch during the thermal history of the Universe. The basic treatment was developed by Lifshitz (1946), Zeldovich (1967) and Field (1974) and has been clearly incorporated in the well-known book by Weinberg (1972). Some more recent books also address this analysis (Kolb and Turner, 1990; Battaner, 1996).

The protogalactic collapse has some differences with respect to the protostellar collapse, mainly:

a) Protostellar collapses are considered to be isothermal, because photons are able to quit the protostellar cloud freely and the temperature remains constant. It is then obtained for Jeans' Mass, M_J $\propto$ $\rho^{1/2}_{}$ . The fact that M_J, the minimum mass able to collapse, increases when the collapse proceeds produces the fragmentation of the cloud until the smaller fragments are so dense that the isothermal regime breaks down. The pre-Recombination collapse involves clouds made up of CDM particles, baryons and, mainly, photons. Photon clouds have no way to remain isothermal when they contract. Adiabatic collapses are to be assumed, which does not lead to any fragmentation.

b) Contraction within the expansion. During the collapse, the dimensionless quantity $\delta$ , defined as $\delta$ = ( $\rho$ - < $\rho$ > )/ < $\rho$ > (where $\rho$ is the inhomogeneity density and < $\rho$ > its mean value in the Universe), increases, but as < $\rho$ > decreases because of the general expansion, $\rho$ need not necessarily increase. The collapse is relative. Indeed, present densities in a galaxy are greater than, but comparable to, densities before the collapse. As a zeroth-order language, isolation rather than absolute contraction gives rise to galaxies. The time evolution of $\delta$ , i.e. of the relative overdensity, provides a simpler description. The effect of expansion is not at all negligible, because the characteristic time of expansion, 1/H, is of the order of the period of Jeans' wave, $\lambda_{J}^{}$ /V_s, where $\lambda_{J}^{}$ is Jeans' wavelength and V_s the speed of sound, with both being variable during history of the Universe.

From the point of view of the physics involved, pre-Recombination collapses require a general-relativistic treatment as they are fluctuations in a very hot medium (photons) and the curvature they produce is not only non-ignorable but a dominant effect.

Jeans' Mass is calculated to be M_J $\propto$ R³ during the era between Annihilation of electrons and positrons and the transition epoch dividing the radiation and matter dominations; R is the cosmological scale factor. Between this last epoch (i.e. Equality) and Recombination, Jeans' Mass increases to a constant asymptotic value, M_J $\approx$ 4 × 10¹⁹M, which is never reached because, at Recombination, the scenario abruptly changes, with a sudden fall from about 10¹⁷M to about 10⁵M. In the post-Recombination era M_J $\propto$ R^-3/2. The complete function M_J(R) is depicted in Fig. 14.

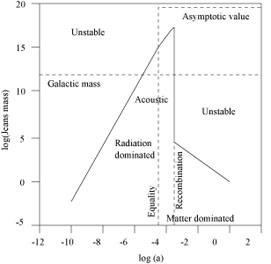
Figure 14. The evolution of Jean's mass as a function of a (the cosmological scale factor taking its present value as unit, i.e. a = R/R₀). Points over the curve correspond to unstable situations leading to gravitational collapse. An inhomogeneity as the Milky Way, with a rest mass of about 10¹²M was unstable until a slightly greater than 10^-6. Then, it underwent acoustic oscillations until the epoch of Recombination, when it become unstable again. Adopted from Battaner (1996).

In this picture, we may follow the stability of an inhomogeneity with a rest mass of 10¹²M, a typical value of the galactic mass, dark matter included. Its mass is in principle higher than Jeans' Mass, and therefore we initially find this protogalaxy in a collapsing phase. The collapse is not so fast, as we will see later, and is truncated when R/R₀ $\sim$ 10^-5 approximately. The proto-galaxy then enters a stable state and Jeans' wave just produces acoustic oscillations. There is not much time to oscillate in this Acoustic era, less than one complete period, because the Recombination sudden falls, leading our homogeneity to unstable conditions again. In other words, once baryons are no longer coupled to photons they are free to collapse.

CDM particles may alter this picture if they have no interaction with photons, as they are free to collapse when they become dominant. They then create potential wells where, after Recombination, the baryons fall. In this case the Acoustic era would be absent.

In the same way that the study of Jeans' waves provides the value of typical stellar masses, it would be desirable to obtain typical values of masses of galaxies and also of clusters and superclusters, because the analysis mentioned considers any inhomogeneity. A large enough mass would always collapse, but we could expect at least a minimum value of collapsed systems.

If the dominant matter particles were baryons, or any other type of particles interacting with photons, then damping by non-perfect fluid effects would affect the oscillations in the Acoustic Era, therefore preventing small mass inhomogeneities from reaching Recombination. The mechanism of photon diffusion is of this type. The fast photons would tend to escape from the overdensity cloud and then push baryons outwards, via the interaction due to Thomson scattering. This is equivalent to a viscosity and a heat conduction, which are expected to be important when the photon mass free time is of the order of the cloud size. The so called Silk Mass is calculated is such a way. Numerical estimations provide values of the Silk Mass of the order of 10¹²M, a very significant value. However, we will see that the model of CDM hierarchical structure formation considers a different scenario, with high masses only being limited by the finite time of the Universe. Even if a mechanism similar to photon diffusion had been at work before Recombination, much smaller masses, much lower than 10¹²M, would be the components of the initial merging CDM blocks. The smaller galaxies are of the order of 10⁷ - 10⁸M.

Another mechanism, called Free Streaming, would give a lower limit to collapsing clouds, if the DM particles were hot. Suppose they were neutrinos, for example; in this case, they would escape from the initial inhomogeneity if this homogeneity were small. When the expansion proceeds and the temperature of the Universe is low enough, the neutrino speed becomes small, which limits the distance a neutrino is able to run. When kT $\sim$ mc², where m is the neutrino's mass, the neutrino can be considered stopped. Normal estimations of the free streaming lower limit mass are of the order of 10¹²M too, although current ideas about the nature of dark matter favour CDM.

Once we have considered the question of when an inhomogeneity is unstable, and therefore when an overdensity region grows and $\delta$ increases, let us briefly speak about the $\delta$ (t) function, or its equivalent, $\delta$ (R). Again a pre-Recombination treatment requires general relativistic tools, Newtonian Mechanics being adequate after Recombination. However, this later epoch is much more complicated from the mathematical point of view, because we know that at present $\delta$ > 1, which means that the evolution is non-linear. In the radiation dominated epoch it was $\delta$ < < 1 and the standard linear perturbation analysis is a very good approximation.

It has been obtained that growth perturbations increase as $\delta$ $\propto$ t, therefore $\delta$ $\propto$ R², during the radiation dominated epoch before entering the Acoustic era. During this Acoustic era, if it really existed, it is apparent that $\delta$ is a constant, or, rather, periodic. After Recombination, inhomogeneities grow as $\delta$ $\propto$ t^2/3, therefore $\delta$ $\propto$ R, until $\delta$ is closer to unity. Then, the simple linear analysis technique is no longer adequate. Non-linear calculations suggest that first $\delta$ $\propto$ R², afterwards $\delta$ $\propto$ R³, but then the hierarchical models, as commented below, constitute the most widely accepted technique to study this recent evolution.

Figure 15 plots $\delta$ (R), but is only a rough description due to the many factors which are at present poorly understood.

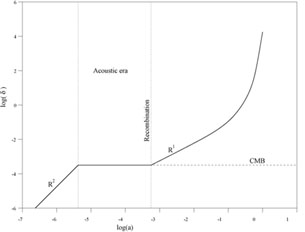
Figure 15. The evolution of the relative overdensity of an inhomogeneity cloud as a function of a = R/R₀, being R the cosmological scale factor and R₀ its present value. Adopted from Battaner (1996).