Magnetic fields in the outermost region of galactic disks

Magnetic fields in the outermost region of galactic disks

Measurements carried out in this zone have not been reported. By roughly interpolating between the large 10 $\mu$ G fields in the inner disk and the lower than 1 $\mu$ G fields outside the galaxy, we cannot exclude fields $\ge$ 1 $\mu$ G in the outermost disk.

Objections to the existence of 1 $\mu$ G fields at large radii could be raised, with the argument that no detectable synchrotron emission has been reported. However, the non-detection of synchrotron emission cannot be interpreted as the absence of magnetic fields. Kronberg (1995) wrote that "synchrotron radiation can tell us only that magnetic field is present, but not measure its strength".

Despite this pessimistic point of view, let us make some simple estimations. When the relativistic electrons responsible for the synchrotron emission have an energy distribution given by NdE = N₀E^-dE, with N₀ and $\gamma$ being constants, then the synchrotron intensity can be calculated with (e.g. Pacholczyk, 1970; Ruzmaikin, Shukurov and Sokoloff, 1988)

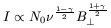
(112)

where B is the component of $\vec{B}\,$ perpendicular to the line-of-sight. The calculation of B once I is measured, is difficult because N_o is unknown. The spectrum of the synchrotron continuum itself [I, $\nu$ ] permits the easy obtention of $\gamma$ , but not of N₀, meaning the number density of relativistic electrons is unknown. To surmount this difficulty the most usual assumption is that of equipartition.

Equipartition is equivalent to the assumption of equal values of the turbulent and magnetic energy densities and that the energy density is the minimum for a given magnetic field, in which case (Ruzmaikin, Shukurov and Sokoloff, 1988)

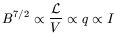
(113)

where $\cal {L}$ is the luminosity of an emitting cloud, V the volume and q the flux.

We will later show that magnetic fields with a gradient slightly less than B $\propto$ R^-1 can produce a flat rotation curve. If for an estimation we take B $\propto$ R^-1, then

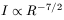
(114)

i.e. I decreases much more rapidly than B does (Lisenfeld, 2000). Therefore, we would not observe synchrotron emission where the magnetic field presents significant values.

The coefficient in (113), I $\propto$ B^7/2, is not perfectly known because it depends on the ratio of protons to electrons in cosmic rays, which has a value in the range 1-100, but following current estimates (Lisenfeld et al. 1996) for a typical VLA beam of 15 arcsec², 2.6 $\mu$ Jy would correspond to 1 $\mu$ G. However, the confusion limit, or minimum detectable flux at, say, 1.5 GHz is about 20 $\mu$ Jy, noticeably larger than the expected 2.6 $\mu$ Jy.

Some works take the equation (112) with a hypothesis about N₀. If relativistic electrons are born in type-II Supernova explosions, which in turn are produced in regions of star formation, i.e. in sites with high gas density, and if relativistic electrons are not able to travel far from the birth region, then N₀ $\propto$ $\rho$ , could be an interesting, simple and acceptable assumption. But in this case, the radial decrease of I would be much faster; much faster even than the exponential (with typical radial scale length about 3 kpc). The reduction of $\rho$ because of the external flaring would give a still faster truncation of the synchrotron continuum. If we assume that type-I Supernovae also contribute to producing relativistic electrons, the truncation of I will be even faster, as a result of the stellar truncation typical in all disks. In the Milky Way it takes place at about 12 kpc (Porcel, Battaner and Jiménez-Vicente, 1997).

Moreover, there is another argument to show that the absence of synchrotron radiation does not imply the absence of magnetic fields. It is observed that the synchrotron spectrum suddenly steepens for large radii. This feature takes place, for instance, in NGC 891 (Hummel et al, 1991; Dahlem, Dettmar and Hummel 1994) for $\ge$ 6 kpc. If the slope of the [logI, log $\nu$ ] curve, usually called $\gamma$ , is high, the number of very high energy electrons is relatively low. It is known (Lisenfeld et al. 1996) that these very high energy electrons have less penetration capacity, i.e. they cannot travel far from their sources. The simplest form of interpreting the increase of $\gamma$ at those radii when the synchrotron becomes undetectable is a truncation of the relativistic electron sources. It is then probable that, the absence of cosmic electrons, rather than the absence of magnetic fields, is responsible for the low synchrotron intensity in the outermost disk.