
| (120) |



In this model by Battaner and Florido (1995) the vertical component of the equation of motion is written as

| (120) |
where vz(R, z) is the vertical velocity,
vA(R) is the Alfven
velocity considered to be a constant in the vertical direction
(because of the assumption
B2 ![]()
![]() ,
as
vA = B/
,
as
vA = B/![]() ); also
); also
![]() = p(R, z)/
= p(R, z)/![]() (R, z) is
assumed to be constant (isothermal condition, or rather, constant
cloud-to-cloud velocity dispersion) and the vertical component of the
gravitational force is simplified to that due to a central point
mass; this assumption is in part justified because it is assumed that
no dark matter halo is present and because we are considering just the
outermost part of the disk. Many of these simplifying conditions are
not necessary and, indeed, are only justified in a model with
exploratory aims.
(R, z) is
assumed to be constant (isothermal condition, or rather, constant
cloud-to-cloud velocity dispersion) and the vertical component of the
gravitational force is simplified to that due to a central point
mass; this assumption is in part justified because it is assumed that
no dark matter halo is present and because we are considering just the
outermost part of the disk. Many of these simplifying conditions are
not necessary and, indeed, are only justified in a model with
exploratory aims.
Therefore the motion in the vertical direction was considered to be
the result of four terms: the inertial term, the magnetic, the
gravitational and the pressure gradient forces. Horizontal velocities
were considered, but the term
vR![]() vz/
vz/![]() z was
neglected.
z was
neglected.
The equation of continuity restricts the possibilities of the vertical flux. It was assumed that
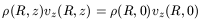
| (121) |
To calculate vz(R, 0) at z = 0 in the
plane (or slightly above the
plane, to avoid the problem arising from the symmetry in the galactic
plane;
vz(R,![]() z) = - vz(R, -
z) = - vz(R, - ![]() z), for very
small
z), for very
small ![]() z, this would imply
vz(R, 0) = 0) some assumptions
must be made; i.e.
adopting a physical mechanism responsible for the vertical flux, which
could be produced by supernova explosions. In this case it would be
preferable to adopt a hypothesis of the type
vz(R, 0)
z, this would imply
vz(R, 0) = 0) some assumptions
must be made; i.e.
adopting a physical mechanism responsible for the vertical flux, which
could be produced by supernova explosions. In this case it would be
preferable to adopt a hypothesis of the type
vz(R, 0) ![]()
![]() ,
if for large time scales supernovae are born where the gas is
denser. Battaner and Florido, instead, considered that Parker
instabilities were the main origin of the vertical flux and assumed
for the flux at z = 0:
,
if for large time scales supernovae are born where the gas is
denser. Battaner and Florido, instead, considered that Parker
instabilities were the main origin of the vertical flux and assumed
for the flux at z = 0:

| (122) |
the value of k being considered a free parameter. This condition is equivalent to

| (123) |
Instead of ![]() , it is preferable to use
, it is preferable to use

| (124) |
because the calculation of ![]() (R, 0) and the profile y(R,
z) were
made using different equations. Using Alfven's velocity the radial
component of the equation of motion is now written as
(R, 0) and the profile y(R,
z) were
made using different equations. Using Alfven's velocity the radial
component of the equation of motion is now written as
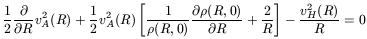
| (125) |
The variable vH(R) is defined by
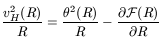
| (126) |
which is what in more conventional theories is called the "halo
velocity" as a way of introducing the halo potential. This quantity
vH(R) was used because it can be found directly
in the literature,
but no dark matter halo was introduced. No inertial terms, neither
vz![]() vR/
vR/![]() z nor
vR
z nor
vR![]() vR/
vR/![]() R, were
considered to be important and the gradient pressure force was again
considered negligible.
R, were
considered to be important and the gradient pressure force was again
considered negligible.
The surface density was adopted from the literature, and therefore
![]()
![]() (R, z)dz was kept constant. To
compensate for the escape, it was assumed that the horizontal flux from
the central region was so easily established that it was able
to supply the necessary escaped mass at all radii. The function
vR(r) was
however found to be negligible. When the vertical velocities reached a
value higher than the typical velocity dispersion, say 8 km/s, gas
clouds were considered to have escaped from the disk, but not necessarily from
the galaxy.
(R, z)dz was kept constant. To
compensate for the escape, it was assumed that the horizontal flux from
the central region was so easily established that it was able
to supply the necessary escaped mass at all radii. The function
vR(r) was
however found to be negligible. When the vertical velocities reached a
value higher than the typical velocity dispersion, say 8 km/s, gas
clouds were considered to have escaped from the disk, but not necessarily from
the galaxy.
Though not affecting the numerical computations, it is interesting to obtain two functions of interest in the interpretation. One of these is the "Flaring Function", Z(R) defined by

| (127) |
and the other is the total mass loss rate

| (128) |
where R0 is the adopted inner boundary
radius. Z(R) is important
because if the disk is highly magnetized, Z(R) can become
unacceptably large. If ![]() is calculated to be too large, the
whole galaxy could evaporate.
is calculated to be too large, the
whole galaxy could evaporate.
A numerical integration of these equations was carried out by Battaner and Florido (1995) taking M31 as a representative galaxy, with a convergent procedure that we do not reproduce here, but just show the results (see Fig. 20).

|
Figure 20. Top left: Alfvén's speed in km s-1 for three values of the free parameter k (10-9, upper curve; 3 × 10-9, middle curve; 10-8cm-1s, lower curve). Top right: Magnetic field strength in gauss. Botton left: The flaring function Z(r) in kpc, for three different values of the free parameter k defined in the text (10-9, upper curve; 3 × 10-9, middle curve; 10-8cm-1s, lower curve). Botton right: Density profiles for the value of the free parameter k = 3 × 10-9cm-1s, for three different values of z=0, 4 and 8 kpc from the galactic plane. From Battaner and Florido (1995). Courtesy of the Royal Astronomical Society. |
The free parameter k should have a value of between
10-9 and
10-8cm-1s, with
k = 3 × 10-9 being the value giving the
most reliable results. The mass loss rate, ![]() was found to
be 0.054, 0.16 and 0.55
M
was found to
be 0.054, 0.16 and 0.55
M![]() yr-1 for
k = 10-9,
3 × 10-9 and
10-8cm-1s; this is still rather low,
lower in
any case than the typical value given by fountain models (15
M
yr-1 for
k = 10-9,
3 × 10-9 and
10-8cm-1s; this is still rather low,
lower in
any case than the typical value given by fountain models (15
M![]() yr-1;
Kahn, 1994).
Part of this gas that escaped from the disk would
eventually fall back into the disk. Even if this were not the case and
in the worst situation in which all the gas escaping from the disk
escaped from the galaxy, the total mass loss during the whole history
of the galaxy (assuming the flux to be constant in time) would be of the
order of 0.16
M
yr-1;
Kahn, 1994).
Part of this gas that escaped from the disk would
eventually fall back into the disk. Even if this were not the case and
in the worst situation in which all the gas escaping from the disk
escaped from the galaxy, the total mass loss during the whole history
of the galaxy (assuming the flux to be constant in time) would be of the
order of 0.16
M![]() yr-1 ×
1010yr
yr-1 ×
1010yr ![]() 1.6 × 109M
1.6 × 109M![]() ,
an acceptable value.
,
an acceptable value.
Even with the simplifying conditions assumed, a coherent general scenario is obtained:
a) The Alfven speed increases outwards is always lower than the
rotational velocity but has a common order of magnitude. B and
![]() decrease but B2/
decrease but B2/![]() increases.
increases.
b) The effect of flaring and escape reduces the magnetic field required
to drive the rotation of the outer disk. In the previous simple model,
6![]() G at 30 kpc was obtained. Now it is a full order of
magnitude less. This is a very exciting figure, as it confirms that
moderate magnetic field strengths can have a decisive influence on the
rotation curve.
G at 30 kpc was obtained. Now it is a full order of
magnitude less. This is a very exciting figure, as it confirms that
moderate magnetic field strengths can have a decisive influence on the
rotation curve.
c) The flaring seems to be high but this is in reasonable agreement with
observations. For low radii, the adoption of the central point mass
potential is not appropriate. For instance, Z(R) is too high for radii
less than about 17 kpc. But in our Galaxy, where precise data exist for
very large radii, a value of Z ![]() 6 kpc at R= 20 kpc from the
plots provided by
Diplas and Savage (1991)
is reproduced by the model fairly well.
6 kpc at R= 20 kpc from the
plots provided by
Diplas and Savage (1991)
is reproduced by the model fairly well.
d) The densities are reasonable. At 30 kpc, values of the order of 1.6 × 10-28gcm-3 (10-4atoms cm-3) were obtained, and at 25 km, 5 × 10-28gcm-3. In any case these values are compatible with the observed surface density, as this function was adopted from the observations.
e) Velocities (vertical at the base of the galactic plane and radial)
are small, of the order of a few km/s, which are nearly undetectable and
therefore do not introduce problems of disagreement with any
measurement. Consider that 2 km/s at z ![]() 0 may produce 10 km/s at
z
0 may produce 10 km/s at
z ![]() 8kpc and
R
8kpc and
R ![]() 20kpc, due to
continuity. (The flux would be conserved, so the decrease in density
accelerates the vertical speed). Velocities of this order of magnitude
are observed even in a quiet disk (see for instance
Jiménez-Vicente et
al. 1999).
20kpc, due to
continuity. (The flux would be conserved, so the decrease in density
accelerates the vertical speed). Velocities of this order of magnitude
are observed even in a quiet disk (see for instance
Jiménez-Vicente et
al. 1999).