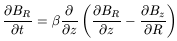
| (129) |
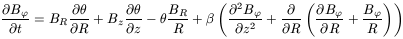
| (130) |
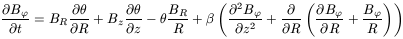
| (131) |



In this Section let us summarize the work by Battaner, Lesch and Florido (1999). The similarities of the strengths in the interstellar, the extragalactic and the pregalactic media suggest a fast and efficient connection between them. In this work, it is proposed that this connection is the result of a highly turbulent magnetic diffusion in the vertical direction.
It is an observational fact that convective phenomena are very active in disks. Galaxies sometimes exhibit "boiling" disks, with NGC 253 being a good example (Sofue, Wakamatsu and Malin, 1994), where dark filaments, lanes, arcs and other micro-structures are features revealing a very complex convective region. This fact is in part explained by "fountain" models (Shapiro and Field, 1976; Breitschwert et al., 1991; Kahn, 1994; Breitschwerdt and Komossa, 1999). Of course, these turbulent motions constitute a transporting of magnetic fields, as a result of the condition of frozen-in lines. Because of this transporting, extra and intergalactic fields merge.
Suppose first that no dynamo is acting on the galactic gas. The equation of induction will tell us (e.g. Ruzmaikin, Shukurov and Sokoloff, 1988; Battaner, 1996)
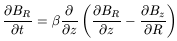
| (129) |
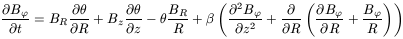
| (130) |
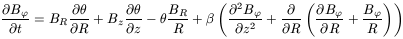
| (131) |
where BR, B![]() and Bz are the
magnetic field strength
components and
and Bz are the
magnetic field strength
components and ![]() is the coefficient of turbulent magnetic
diffusion. Cylindrical symmetry has been assumed. The usual expression
to calculate
is the coefficient of turbulent magnetic
diffusion. Cylindrical symmetry has been assumed. The usual expression
to calculate ![]() is
is
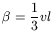
| (132) |
where l is a typical length of the larger convective cells, say
l ![]() 1kpc, and v is a typical convection
velocity corresponding
to the larger scale turbulence, say 20 km s-1. Hence
1kpc, and v is a typical convection
velocity corresponding
to the larger scale turbulence, say 20 km s-1. Hence ![]() is
of the order of
2 × 1027cm2s-1
is
of the order of
2 × 1027cm2s-1 ![]() 6kpc2Gyr-1. In
comparison,
6kpc2Gyr-1. In
comparison, ![]() is taken as being of the order of
1026cm2s-1 in the inner
disk), of
5 × 1027cm2s-1 in
the galactic corona and of
8 × 1029cm2s-1 in the
intergalactic medium in a cluster
(Ruzmaikin, Sokoloff and
Shukurov, 1989;
Sokoloff and Shukurov, 1990;
Ruzmaikin, Shukurov and
Sokoloff, 1988).
is taken as being of the order of
1026cm2s-1 in the inner
disk), of
5 × 1027cm2s-1 in
the galactic corona and of
8 × 1029cm2s-1 in the
intergalactic medium in a cluster
(Ruzmaikin, Sokoloff and
Shukurov, 1989;
Sokoloff and Shukurov, 1990;
Ruzmaikin, Shukurov and
Sokoloff, 1988).
The characteristic diffusion time is calculated with
l2/![]() ,
therefore having a typical value of 0.2 Gyr, very little compared with
the lifetime of the galaxy. Extragalactic magnetic fields would have spatial
variations at scales much larger than a galaxy. The field strength
can be assumed to be constant outside the galaxy, as a boundary
condition. This external steady state magnetic field could have
produced an initial penetration of magnetic fields which would have
been subsequently ordered by differential rotation, resulting in a
predominantly toroidal field. Or rather, the disk was born out of already
magnetized material, then was magnetized at birth and maintains a
permanent interchange with the magnetized environment, because of the
high magnetic diffusivity.
,
therefore having a typical value of 0.2 Gyr, very little compared with
the lifetime of the galaxy. Extragalactic magnetic fields would have spatial
variations at scales much larger than a galaxy. The field strength
can be assumed to be constant outside the galaxy, as a boundary
condition. This external steady state magnetic field could have
produced an initial penetration of magnetic fields which would have
been subsequently ordered by differential rotation, resulting in a
predominantly toroidal field. Or rather, the disk was born out of already
magnetized material, then was magnetized at birth and maintains a
permanent interchange with the magnetized environment, because of the
high magnetic diffusivity.
However, the magnetic field is assumed to be homogeneous outside and toroidal inside. A configuration that continuously transforms a constant into a toroidal field was proposed by Battaner and Jiménez-Vicente (1998), but here we need to adopt convenient boundary conditions taken at a large enough height.
All three components -Bx, By, Bz- are constant in the extragalactic medium. But not all penetrate and diffuse inwards equally. For instance, there is no difficulty for Bz to penetrate, because it is not perturbed by rotation. And if the transport is so effective we could even assume that Bz is a constant in the whole outer disk considered, equal to the extragalactic value of Bz. We then assume as a reasonable mathematical assumption that Bz=cte everywhere in the integration region.
It is more difficult for the other components to penetrate (or exit). For
instance, BR penetrates into the disk at a given time
and point (R,
![]() ); the rotation would transport the frozen-in magnetic
field
lines into the azimuthally opposite position (R,
); the rotation would transport the frozen-in magnetic
field
lines into the azimuthally opposite position (R,
![]() +
+ ![]() ) in
half a rotation period. The direction of the penetrated field
vector there would be opposite to the vector transported from the
opposite azimuth. The two vectors would meet with the
same modulus and opposite direction and would destroy one another
through the reconnection of field lines. It is therefore
tempting, in a first simplified model, to assume that
BR = 0, at
the boundaries. We may even adopt BR = 0 everywhere
inside the disk.
) in
half a rotation period. The direction of the penetrated field
vector there would be opposite to the vector transported from the
opposite azimuth. The two vectors would meet with the
same modulus and opposite direction and would destroy one another
through the reconnection of field lines. It is therefore
tempting, in a first simplified model, to assume that
BR = 0, at
the boundaries. We may even adopt BR = 0 everywhere
inside the disk.
With respect to B![]() , we have a similar situation. B
, we have a similar situation. B![]() when penetrating at (R,
when penetrating at (R, ![]() ) would be frozen-in transported to (R,
) would be frozen-in transported to (R,
![]() +
+ ![]() ) in half a rotation and then interact with the field
penetrated there. Reconnection would then act and we could reasonably
adopt
B
) in half a rotation and then interact with the field
penetrated there. Reconnection would then act and we could reasonably
adopt
B![]() = 0 at the boundaries. But
B
= 0 at the boundaries. But
B![]() is easily
amplified by rotation and can be generated from Bz,
which is non-vanishing; therefore we cannot assume
B
is easily
amplified by rotation and can be generated from Bz,
which is non-vanishing; therefore we cannot assume
B![]() = 0 everywhere;
rather it is
B
= 0 everywhere;
rather it is
B![]() (R, z) that we want to
calculate. We also assume
steady-state conditions,
(R, z) that we want to
calculate. We also assume
steady-state conditions,
![]() /
/![]() t = 0. The equations then
become greatly simplified which also permits a simplified
interpretation of what is essential in the process, much more
understandable than a lengthy numerical calculation. In the above
equations, we set
t = 0. The equations then
become greatly simplified which also permits a simplified
interpretation of what is essential in the process, much more
understandable than a lengthy numerical calculation. In the above
equations, we set
![]() /
/![]() t = 0, Bz=constant,
BR = 0 and obtain
t = 0, Bz=constant,
BR = 0 and obtain
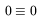
| (133) |
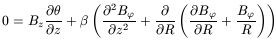
| (134) |
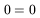
| (135) |
The first and third are tautologic, telling us that we could have deduced much of what was assumed (as Battaner, Lesch and Florido did), but that is unimportant. We now see that our assumptions do not lead to incoherent results.
The second equation would provide us with B![]() if
if ![]() (z) were
known. Let us further assume
(z) were
known. Let us further assume
![]()
![]() /
/![]() z = 0, which is
not unrealistic given the relatively low thickness of the disk. In order
to find a fast solution (which is not necessary, but just didactic)
let us assume that
z = 0, which is
not unrealistic given the relatively low thickness of the disk. In order
to find a fast solution (which is not necessary, but just didactic)
let us assume that
![]() B
B![]() /
/![]() z2 is
negligible (it cannot be zero, as B
z2 is
negligible (it cannot be zero, as B![]() must be zero at the
boundary). In fact,
some galaxies have a radio halo (e.g. NGC 253,
Beck et al. 1994;
NGC 891,
Dahlem, Lisenfeld and Golla, 1995
in other spirals). The decrease of magnetic field strength with z is
observed to be very slow, even in galaxies with no radio halo
(Ruzmaikin et al., 1988;
Wielebinski, 1993)
and also in the Milky Way
(Han and Qiao, 1994).
Then for small
| z | we simply obtain
must be zero at the
boundary). In fact,
some galaxies have a radio halo (e.g. NGC 253,
Beck et al. 1994;
NGC 891,
Dahlem, Lisenfeld and Golla, 1995
in other spirals). The decrease of magnetic field strength with z is
observed to be very slow, even in galaxies with no radio halo
(Ruzmaikin et al., 1988;
Wielebinski, 1993)
and also in the Milky Way
(Han and Qiao, 1994).
Then for small
| z | we simply obtain
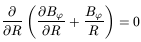
| (136) |
therefore
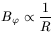
| (137) |
which is precisely the critical profile. Once we see how the critical profile is supported with this mechanism, it is expected that other more realistic calculations would be able to provide sub-critical profiles, capable therefore of producing inward magnetic forces.
The symmetries of the magnetic field predicted in this simple model agree with those obtained with Faraday rotation by Han et al. (1997) in our own galaxy. This model does not need a dynamo but provides a large-scale structure with much in common with the so called AO mode. We also predict an antisymmetry of the azimuthal field in both hemispheres for | l | < 90o. This AO dynamo mode has also been observed in other galaxies, but in view of the symmetry similarities with our predictions, these galaxies could be interpreted in terms of the mechanisms sought by Battaner, Lesch and Florido (1999).