Copyright © 1984 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1984. 22:
319-58 Copyright © 1984 by Annual Reviews. All rights reserved |
Without direct velocity indicators such as emission lines from material in the jet flows, estimates of the average flow velocities vj are indirect and sensitive to the initial assumptions. Most methods assume jet properties to be stationary in time and estimate vj from observables using one or more of the following arguments.
6.1.1 ENERGY FLUX If synchrotron losses
from a lobe of luminosity Llobe are
continuously replenished by the energy influx from a jet at an
efficiency epsilon, the energy flux supplied to the lobe must be
Lj = Llobe /
 . The flux
Lj is related to other jet parameters by
. The flux
Lj is related to other jet parameters by
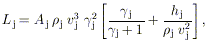
|
where
Aj, vj,
 j,
j,
 j, and
hj are the cross-sectional area, flow
velocity, density, Lorentz factor, and enthalpy per unit rest mass of
the jet at some point along it, respectively. (The transverse
structure of the jet is usually ignored when estimating
vj.)
j, and
hj are the cross-sectional area, flow
velocity, density, Lorentz factor, and enthalpy per unit rest mass of
the jet at some point along it, respectively. (The transverse
structure of the jet is usually ignored when estimating
vj.)
6.1.2 MOMENTUM FLUX For jets which
terminate at hot spots, the thrust
Tj / h in the rest
frame of the hot spot must balance
ph AH, where
p h and Ah are the
minimum pressure and cross-sectional area of the hot spot estimated
from its synchrotron parameters. The thrust
Tj = Aj
 j
vj2
j
vj2
 j2 in the
galaxy or QSR frame can be calculated from this by assuming the
dynamics of the interaction between the hot spot and the ambient density
j2 in the
galaxy or QSR frame can be calculated from this by assuming the
dynamics of the interaction between the hot spot and the ambient density
 e to
relate vj to the velocity v h
of advance of the hot
spot. Estimates for Tj can also be made for C-shaped
jets in
"head-tail" sources if these jets are bent by the ram pressure of an
intergalactic density
e to
relate vj to the velocity v h
of advance of the hot
spot. Estimates for Tj can also be made for C-shaped
jets in
"head-tail" sources if these jets are bent by the ram pressure of an
intergalactic density
 e
through which their parent galaxy moves at velocity vg
(10,
128).
If the radius of curvature of the C-structure
is Rc and the scale over which the ram pressure is
transmitted to the jet is H, momentum balance requires that
Tj =
e
through which their parent galaxy moves at velocity vg
(10,
128).
If the radius of curvature of the C-structure
is Rc and the scale over which the ram pressure is
transmitted to the jet is H, momentum balance requires that
Tj =
 e
vg2 Aj
Rc / H. The
parameter H is the radius Rj of the jet in the
"naked" jet-bending model of
(10),
but it is a scale associated with the ISM of the parent
galaxy in the "shielded" model of
(128).
e
vg2 Aj
Rc / H. The
parameter H is the radius Rj of the jet in the
"naked" jet-bending model of
(10),
but it is a scale associated with the ISM of the parent
galaxy in the "shielded" model of
(128).
6.1.3 MASS FLUX The mass flux
dm / dt = Aj
 j
vj
j
vj
 j down the jet
must meet either
reasonable constraints on the rate of ejection from the "central
engine" or constraints from depolarization data on the total mass
injected into the lobes over the lifetime of the source. (The latter
constraints are generally less stringent, but they could be tightened
by high-resolution polarimetry of lobes at frequencies below 1 GHz.)
j down the jet
must meet either
reasonable constraints on the rate of ejection from the "central
engine" or constraints from depolarization data on the total mass
injected into the lobes over the lifetime of the source. (The latter
constraints are generally less stringent, but they could be tightened
by high-resolution polarimetry of lobes at frequencies below 1 GHz.)
6.1.4 JET EXPANSION The Mach number
Mj of a free jet where it detached from its
confinement (Section 4.1) can be
estimated from its synchrotron expansion rate via
d /
d
/
d = (2 /
Mj)sec(i), where
i is the (assumed)
angle between the jet axis and the plane of the sky. Then
vj = Mj
sqrt[
= (2 /
Mj)sec(i), where
i is the (assumed)
angle between the jet axis and the plane of the sky. Then
vj = Mj
sqrt[ pj /
pj /
 j],
where
j],
where  is the
ratio of principal specific heats in the jet,
and a lower limit to pj is obtained from the synchrotron
parameters. If the jet is actually confined, Mj is
overestimated. If
the weak radio galaxy jets are alternately free and confined
(Section 4.1.1), Mj
is best indicated by the rapid expansions at
z
is the
ratio of principal specific heats in the jet,
and a lower limit to pj is obtained from the synchrotron
parameters. If the jet is actually confined, Mj is
overestimated. If
the weak radio galaxy jets are alternately free and confined
(Section 4.1.1), Mj
is best indicated by the rapid expansions at
z  1 - 10
kpc, which imply that
Mj
1 - 10
kpc, which imply that
Mj  10
there.
10
there.
6.1.5 ELIMINATING THE JET DENSITY
Usage of
the techniques of Sections 6.1.1 -
6.1.4 alone requires estimates of
 j,
generally from centimeter-wavelength Faraday
depolarization data that are hard to obtain and to interpret
(87).
High signal-to-noise is needed to reduce Ricean bias in the
polarized signal
(183,
270).
The configuration of Bj is unclear
(Section 3.2), particularly the scale
distribution of its reversals,
which may "hide" thermal gas. Some jets are surrounded by
emission-line filaments (Section 5.1.2)
and magnetoionic media with clumping scales of ~ 1 - 5 kpc
(33,
183;
Table 1, ref. L2). Differential
Faraday rotation across the radio beam by such media may decouple the
observed depolarization from
j,
generally from centimeter-wavelength Faraday
depolarization data that are hard to obtain and to interpret
(87).
High signal-to-noise is needed to reduce Ricean bias in the
polarized signal
(183,
270).
The configuration of Bj is unclear
(Section 3.2), particularly the scale
distribution of its reversals,
which may "hide" thermal gas. Some jets are surrounded by
emission-line filaments (Section 5.1.2)
and magnetoionic media with clumping scales of ~ 1 - 5 kpc
(33,
183;
Table 1, ref. L2). Differential
Faraday rotation across the radio beam by such media may decouple the
observed depolarization from
 j, so
even setting limits to
j, so
even setting limits to
 j from
low-resolution depolarization data without mapping the rotation
measure gradients is hazardous, especially at low frequencies. The
methods in Section 6.1.1 - 6.1.4
all permit vj -> c if
j from
low-resolution depolarization data without mapping the rotation
measure gradients is hazardous, especially at low frequencies. The
methods in Section 6.1.1 - 6.1.4
all permit vj -> c if
 j -> 0,
but Table 4 shows how vj can be
constrained using combinations of these methods to eliminate
j -> 0,
but Table 4 shows how vj can be
constrained using combinations of these methods to eliminate
 j for
"cold" (hj <<
j for
"cold" (hj <<
 j
vj2) jets. As
hj /
j
vj2) jets. As
hj /
 j
vj2 =
j
vj2 =
 /
Mj2(
/
Mj2( - 1)
from the gas laws and Section 6.1.4, this is a good
assumption for jets with
Mj
- 1)
from the gas laws and Section 6.1.4, this is a good
assumption for jets with
Mj  4. These
combinations also eliminate Aj, bypassing the
(uncertain) relationship between the jet's synchrotron width
4. These
combinations also eliminate Aj, bypassing the
(uncertain) relationship between the jet's synchrotron width
 and its
flow radius Rj. They normally yield velocities in the
range 1000 < vj < 30,000 km s-1
unless low efficiencies
and its
flow radius Rj. They normally yield velocities in the
range 1000 < vj < 30,000 km s-1
unless low efficiencies
 or high mass fluxes
dm/dt are assumed.
or high mass fluxes
dm/dt are assumed.
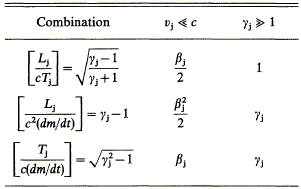
|
6.1.6 SUPERLUMINAL MOTION A simple model
for the observed proper motions of knots in compact
sources (57)
is that apparent "superluminal" motion at
 app =
vapp/c > 1
arises for features in the approaching side of a high-
app =
vapp/c > 1
arises for features in the approaching side of a high-
 j jet at a
large angle i to the plane of the sky, whereupon
vj = vapp /
[
j jet at a
large angle i to the plane of the sky, whereupon
vj = vapp /
[ app sin(i)
+ cos(i)].
app sin(i)
+ cos(i)].
6.1.7 DOPPLER BOOSTING With the above
notation, vj is related to the ratio of intensities
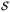 app of the
approaching and receding sides of an intrinsically symmetric
(
app of the
approaching and receding sides of an intrinsically symmetric
(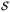 = 1) jet as
vj sin(i) =
c[
= 1) jet as
vj sin(i) =
c[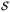 app
app - 1] /
[
- 1] /
[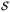 app
app + 1], where
+ 1], where
 = 1 / (2 +
= 1 / (2 +
 ) for a continuous jet with a
) for a continuous jet with a
 -
- spectrum (23).
Assuming
spectrum (23).
Assuming 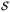 app
to be due entirely to Doppler boosting therefore constrains
app
to be due entirely to Doppler boosting therefore constrains
 jsin(i). Note that with the typical value
jsin(i). Note that with the typical value
 = 0.65
(Section 4.2),
= 0.65
(Section 4.2),
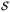 app varies as
app varies as
 j5.3
if the line of sight is
< 1/
j5.3
if the line of sight is
< 1/ j radians
from the jet
axis; also, note that a jet can be "one sided" as in
Section 3.1
(
j radians
from the jet
axis; also, note that a jet can be "one sided" as in
Section 3.1
(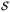 app > 4 : 1)
if
app > 4 : 1)
if  j sin(i)
> 0.26, which at i = 30° (the median value for
randomly oriented sources) requires only that
j sin(i)
> 0.26, which at i = 30° (the median value for
randomly oriented sources) requires only that
 j > 0.52.
j > 0.52.
6.1.8 JET WIGGLING Many jets wiggle
around their mean direction (e.g.
29,
172,
183,
214,
220,
262,
263).
Mechanisms for periodic lateral deflections
 as
a function of angle
as
a function of angle  from
the core [reviewed in
(252)]
include (a)
orbital motion of the primary collimator around a companion mass in
the parent nucleus
(9,
151)
or a nearby member of the same group or cluster
(22,
263);
(b) precession of the primary collimator or of a
larger-scale recollimating atmosphere due to interaction with another
body
(9,
104,
123,
143,
205,
284);
and (c) growth of helical
Kelvin-Helmholtz instabilities at the boundary of a confined jet
(Section 6.4). Pure orbital motion leads to
C-symmetry between the two sides of a jet, with fixed wiggle amplitude
from
the core [reviewed in
(252)]
include (a)
orbital motion of the primary collimator around a companion mass in
the parent nucleus
(9,
151)
or a nearby member of the same group or cluster
(22,
263);
(b) precession of the primary collimator or of a
larger-scale recollimating atmosphere due to interaction with another
body
(9,
104,
123,
143,
205,
284);
and (c) growth of helical
Kelvin-Helmholtz instabilities at the boundary of a confined jet
(Section 6.4). Pure orbital motion leads to
C-symmetry between the two sides of a jet, with fixed wiggle amplitude
 and a period
and a period
 0. Pure
precession of the source of a free nonrelativistic jet leads to
S-symmetry, linear growth of
0. Pure
precession of the source of a free nonrelativistic jet leads to
S-symmetry, linear growth of  with
with  , and a period
, and a period
 p. The analogue
for relativistic jets is more complicated as the S-symmetry is broken
by light travel time effects, which might themselves indicate
vj if other distortions were absent
(63,
104,
143).
Helical surface
instabilities on a confined expanding jet make wiggles whose
amplitudes
p. The analogue
for relativistic jets is more complicated as the S-symmetry is broken
by light travel time effects, which might themselves indicate
vj if other distortions were absent
(63,
104,
143).
Helical surface
instabilities on a confined expanding jet make wiggles whose
amplitudes  and wavelengths
and wavelengths
 i both grow with
i both grow with
 ; linear theory has
been used to estimate the most rapidly growing wavelength
; linear theory has
been used to estimate the most rapidly growing wavelength
 i as a
function of jet radius Rj, Mach number
Mj, and density contrast
i as a
function of jet radius Rj, Mach number
Mj, and density contrast
 j /
j /
 e
(Section 6.4).
e
(Section 6.4).
Attempts to constrain vj from jet-wiggling data "match" an
observed pattern
 (
( ) to one of these pure forms to
find a characteristic wavelength
) to one of these pure forms to
find a characteristic wavelength
 0 and a
self-consistent estimate of the characteristic
period
0 and a
self-consistent estimate of the characteristic
period  0 or
0 or
 p. Then,
vj or Mj is
derived from one of the following: vj =
p. Then,
vj or Mj is
derived from one of the following: vj =
 0 /
0 /
 0,
vj =
0,
vj =
 0 /
0 /
 p, or
p, or
 0
0

 i =
Rj F1 (Mj)
F2(
i =
Rj F1 (Mj)
F2( j /
j /
 e),
where the
functions F1 and F2 are provided by
(linear) instability theory. These
methods are fraught with uncertainties. Well-studied jets rarely match
simple orbital or ballistic precessional shapes convincingly
(22,
104,
105,
257),
so additional poorly constrained parameters (e.g. multiple
or eccentric orbits, variation of precession cone angle with time) are
invoked. Even goodness of fit to a simple C- or S-shape does not
guarantee uniqueness of the model
(63,
122).
Bending and buoyancy effects (e.g.
119,
235,
283)
may also be present and - unless the jet
is denser than the ambient medium - lateral motions may excite surface
instabilities, whose growth also alters the shape of the jet
(12).
Linear instability theory may be inadequate to describe any mode that
grows sufficiently to become detectable on radio maps.
e),
where the
functions F1 and F2 are provided by
(linear) instability theory. These
methods are fraught with uncertainties. Well-studied jets rarely match
simple orbital or ballistic precessional shapes convincingly
(22,
104,
105,
257),
so additional poorly constrained parameters (e.g. multiple
or eccentric orbits, variation of precession cone angle with time) are
invoked. Even goodness of fit to a simple C- or S-shape does not
guarantee uniqueness of the model
(63,
122).
Bending and buoyancy effects (e.g.
119,
235,
283)
may also be present and - unless the jet
is denser than the ambient medium - lateral motions may excite surface
instabilities, whose growth also alters the shape of the jet
(12).
Linear instability theory may be inadequate to describe any mode that
grows sufficiently to become detectable on radio maps.
The above methods give velocities ranging from
vj  1000
km s-1 in C-shaped jets in head-tail sources (using
Section 6.1.2) to
1000
km s-1 in C-shaped jets in head-tail sources (using
Section 6.1.2) to
 c (using
Section 6.1.6 to interpret one sidedness or
Section 6.1.7 to interpret
superluminal motion). This uncertainty in vj seriously
obstructs progress in elucidating the physics of radio jets.
c (using
Section 6.1.6 to interpret one sidedness or
Section 6.1.7 to interpret
superluminal motion). This uncertainty in vj seriously
obstructs progress in elucidating the physics of radio jets.
6.2.1 ARGUMENTS FOR vj
 c ON PARSEC
SCALES Five arguments favor
vj
c ON PARSEC
SCALES Five arguments favor
vj  c on parsec scales in some sources:
c on parsec scales in some sources:
 j
j
 2.5 - 10 (for
H0 = 100) and these structures are within
1 /
2.5 - 10 (for
H0 = 100) and these structures are within
1 / i radians of
the line of sight (Section 6.1.6).
i radians of
the line of sight (Section 6.1.6).
 j)
may explain the
high brightness temperatures implied by the rapid low-frequency
variability of some compact radio sources
(89,
and references therein).
j)
may explain the
high brightness temperatures implied by the rapid low-frequency
variability of some compact radio sources
(89,
and references therein).
 90°) required by this
interpretation of the properties of strong compact cores are
consistent with the large apparent bending of the jets in
core-dominated sources (Section 3.3).
90°) required by this
interpretation of the properties of strong compact cores are
consistent with the large apparent bending of the jets in
core-dominated sources (Section 3.3).
There is little evidence against
vj  c on parsec scales: 3C 147 has
a complex, two-sided parsec-scale structure
(194),
but two sidedness
may be ascribed to bending a one-sided jet across the line of sight,
in a suitably small number of cases, without endangering the
relativistic-jet picture of compact sources.
c on parsec scales: 3C 147 has
a complex, two-sided parsec-scale structure
(194),
but two sidedness
may be ascribed to bending a one-sided jet across the line of sight,
in a suitably small number of cases, without endangering the
relativistic-jet picture of compact sources.
6.2.2 ARGUMENTS AGAINST vj
 c ON
KILOPARSEC SCALES The sensitivity of Doppler boosting
(Section 6.1.7) to vjsin(i)
argues against vj
c ON
KILOPARSEC SCALES The sensitivity of Doppler boosting
(Section 6.1.7) to vjsin(i)
argues against vj
 c in the C-shaped
jets in "narrow head-tail"
sources. If these are indeed swept back by ram pressure of the
intergalactic medium (Section 6.1.2),
vj changes direction along them by as much as 90°
(e.g.
171,
214,
257).
If vj
c in the C-shaped
jets in "narrow head-tail"
sources. If these are indeed swept back by ram pressure of the
intergalactic medium (Section 6.1.2),
vj changes direction along them by as much as 90°
(e.g.
171,
214,
257).
If vj
 c, they would
(a) have
large side-to-side asymmetries and (b) brighten or fade dramatically
as they bend, in conflict with observation
(265).
The orientations of
dust lanes in some weak radio galaxies also suggest that brightness
asymmetry at the bases of their two-sided jets
(Section 3.1) is
unlikely to be due to Doppler favoritism. The jets are generally
> 70° from the dust lanes in projection
(134
and Table 1, ref. L1), so they
should generally be nearly perpendicular to them in three
dimensions. The orientation of the dust lane
(266)
in M84 thereby
suggests that the northern jet, which is the brighter and has the
one-sided base (Figure 1), is either
receding or very close to the
plane of the sky (if it is an outflow). Both this constraint and the
fact that it becomes two sided without bending argue that its greater
brightness is due to greater power output or greater dissipation on
its side of the nucleus, rather than to Doppler boosting. R.A. Laing
(personal communication) finds similar results in NGC 3665 and for the
possible jet in NGC 612, although in Cen A the peculiar velocities of
the optical filaments (Section 5.1.2)
argue that the bright radio jet is approaching.
c, they would
(a) have
large side-to-side asymmetries and (b) brighten or fade dramatically
as they bend, in conflict with observation
(265).
The orientations of
dust lanes in some weak radio galaxies also suggest that brightness
asymmetry at the bases of their two-sided jets
(Section 3.1) is
unlikely to be due to Doppler favoritism. The jets are generally
> 70° from the dust lanes in projection
(134
and Table 1, ref. L1), so they
should generally be nearly perpendicular to them in three
dimensions. The orientation of the dust lane
(266)
in M84 thereby
suggests that the northern jet, which is the brighter and has the
one-sided base (Figure 1), is either
receding or very close to the
plane of the sky (if it is an outflow). Both this constraint and the
fact that it becomes two sided without bending argue that its greater
brightness is due to greater power output or greater dissipation on
its side of the nucleus, rather than to Doppler boosting. R.A. Laing
(personal communication) finds similar results in NGC 3665 and for the
possible jet in NGC 612, although in Cen A the peculiar velocities of
the optical filaments (Section 5.1.2)
argue that the bright radio jet is approaching.
This evidence against
vj  c in sources with
Ptot1.4 < 1025 W
Hz-1 (FR I
structures) leaves open the possibility that vj
increases with Ptot, so
that the long one-sided jets in powerful sources might be
Doppler-boosted flows with
c in sources with
Ptot1.4 < 1025 W
Hz-1 (FR I
structures) leaves open the possibility that vj
increases with Ptot, so
that the long one-sided jets in powerful sources might be
Doppler-boosted flows with
 j >>
1. Some bent one-sided jets have
smooth brightness variations [e.g. 1150 + 497
(Figure 3), 4C 32.69
(191)],
which are inconsistent with changing Doppler boosts in
high-
j >>
1. Some bent one-sided jets have
smooth brightness variations [e.g. 1150 + 497
(Figure 3), 4C 32.69
(191)],
which are inconsistent with changing Doppler boosts in
high- j
jets if they bend because they are confined. Such jets could be
ballistic, however, with their shapes arising from wobble
(precession?) of the primary collimator;
vj would then not follow the
bends, but the wiggle pattern would move radially as a whole. Changes
in vjsin(i) and in the Doppler boosting
(Section 6.1.7) may then be
small. We must know whether or not such jets are confined
(Section 4.1), and if so where, to decide
whether their brightness distributions argue against vj
j
jets if they bend because they are confined. Such jets could be
ballistic, however, with their shapes arising from wobble
(precession?) of the primary collimator;
vj would then not follow the
bends, but the wiggle pattern would move radially as a whole. Changes
in vjsin(i) and in the Doppler boosting
(Section 6.1.7) may then be
small. We must know whether or not such jets are confined
(Section 4.1), and if so where, to decide
whether their brightness distributions argue against vj
 c. Doppler boosting
models for long
one-sided jets also require large angles i, so boosted one-sided jets
would be significantly longer in three dimensions than they appear in
projection. It is unclear whether this seriously conflicts with
vj
c. Doppler boosting
models for long
one-sided jets also require large angles i, so boosted one-sided jets
would be significantly longer in three dimensions than they appear in
projection. It is unclear whether this seriously conflicts with
vj  c
in these jets, as the existing statistics of QSR source sizes come
from samples containing significant numbers of one-sided jets
(Section 2.2). Maps with greater dynamic
range are needed to assess the degree
of one sidedness of these jets (we do not know by how much
c
in these jets, as the existing statistics of QSR source sizes come
from samples containing significant numbers of one-sided jets
(Section 2.2). Maps with greater dynamic
range are needed to assess the degree
of one sidedness of these jets (we do not know by how much
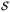 > 4 in
most cases), as the average deprojection increases with the average
asymmetry.
> 4 in
most cases), as the average deprojection increases with the average
asymmetry.
6.2.3 ARGUMENTS FOR vj
 c ON KILOPARSEC
SCALES Table 1 lists 22
sources with VLBI jets or elongations. Of these,
five exhibit superluminal expansion - 3C 120, 3C 179, 3C 273, 3C 279,
3C 345
(57).
In all five, the kiloparsec- and parsec-scale jets start
on the same side of the core, as in
Figure 4 (see references in
Table 1). Sixteen others have VLBI
elongations and kiloparsec-scale jets,
but their proper motions on parsec scales are unknown. In 11 of these
(NGC 315, 3C78, 3C84, 0957 + 56, 3C111, M87, Cen A, NGC 6251, 3C371,
3C405, and 3C418), the larger-scale jet starts on the same side
as the
small, e.g. Figures 2 and
5. Of the remaining five, two (3C 147 and
3C236) have two-sided small-scale structure, two (M84 and 3C 454.3) do
not have closure-phase VLBI maps, and 3C 309.1 has complex
structure. The correlation between small- and large-scale sidedness
argues that one sidedness has the same cause on both scales. It
supports the idea that vj can be high enough on kiloparsec
scales for Doppler favoritism to be important, if one is convinced by
the case for
c ON KILOPARSEC
SCALES Table 1 lists 22
sources with VLBI jets or elongations. Of these,
five exhibit superluminal expansion - 3C 120, 3C 179, 3C 273, 3C 279,
3C 345
(57).
In all five, the kiloparsec- and parsec-scale jets start
on the same side of the core, as in
Figure 4 (see references in
Table 1). Sixteen others have VLBI
elongations and kiloparsec-scale jets,
but their proper motions on parsec scales are unknown. In 11 of these
(NGC 315, 3C78, 3C84, 0957 + 56, 3C111, M87, Cen A, NGC 6251, 3C371,
3C405, and 3C418), the larger-scale jet starts on the same side
as the
small, e.g. Figures 2 and
5. Of the remaining five, two (3C 147 and
3C236) have two-sided small-scale structure, two (M84 and 3C 454.3) do
not have closure-phase VLBI maps, and 3C 309.1 has complex
structure. The correlation between small- and large-scale sidedness
argues that one sidedness has the same cause on both scales. It
supports the idea that vj can be high enough on kiloparsec
scales for Doppler favoritism to be important, if one is convinced by
the case for
 j >> 1 on
parsec scales (Section 6.2.1). This case
is strongest
for the five superluminal sources, but it is not yet impregnable.
Since there are no known coreless large-scale jets, either both the
cores and the jets are Doppler boosted or the luminosities of
intrinsically one-sided jets are coupled to those of the cores; the
reason for such coupling over such a wide range of linear scales is
unclear if the sidedness is due to asymmetric dissipation. If the
kiloparsec-scale sidedness is intrinsic
(124,
213,
218,
273,
280),
these data require a switching time-scale
j >> 1 on
parsec scales (Section 6.2.1). This case
is strongest
for the five superluminal sources, but it is not yet impregnable.
Since there are no known coreless large-scale jets, either both the
cores and the jets are Doppler boosted or the luminosities of
intrinsically one-sided jets are coupled to those of the cores; the
reason for such coupling over such a wide range of linear scales is
unclear if the sidedness is due to asymmetric dissipation. If the
kiloparsec-scale sidedness is intrinsic
(124,
213,
218,
273,
280),
these data require a switching time-scale
 >
dj/vj
and an alternative model for superluminal expansions. The constraint
>
dj/vj
and an alternative model for superluminal expansions. The constraint
 >
dj/vj is often
hard to reconcile with
>
dj/vj is often
hard to reconcile with  being
less than the synchrotron lifetimes in the hot spots (e.g.
113,
265).
On balance, the correlation between
parsec and kiloparsec sidedness favors
being
less than the synchrotron lifetimes in the hot spots (e.g.
113,
265).
On balance, the correlation between
parsec and kiloparsec sidedness favors
 core
core

 j
j
 1 in powerful sources.
1 in powerful sources.
Other (weaker) arguments for
vj  c on kpc scales are the following:
c on kpc scales are the following:
6.3. Jet/Hot-Spot Symmetries and the Sidedness Dilemma
The symmetries of the regions where powerful jets end may also offer
clues to the reasons for their one sidedness
(215).
If it is always
due to Doppler favoritism, the jetted and unjetted lobes should look
similar - unless
high- j jets push
the hot spots out at
vh
j jets push
the hot spots out at
vh  c, in
which case the brighter jet should appear to feed the brighter and
more distant hot spot if the two sides of the source have the same
history (146).
(In the extreme case of a "young"
high-
c, in
which case the brighter jet should appear to feed the brighter and
more distant hot spot if the two sides of the source have the same
history (146).
(In the extreme case of a "young"
high- j
source,
radiation from the receding side may also not yet have reached us.)
j
source,
radiation from the receding side may also not yet have reached us.)
In 34 of the 46 FR II sources in Table 1 with one-sided jets, one lobe has a significantly brighter hot spot than the other on the highest resolution map available. Seventeen of the 34 have fC = Score5 / Stot1.4 > 0.05; the brighter jet points to the brighter hot spot in 16 of these. Unless the jets are "young", either the brighter jet has a higher thrust or the jets and the hot spots in these sources are both Doppler boosted. In the 17 cases with fC < 0.05, the brighter jet points to the brighter hot spot in ten and to the weaker in seven. This is consistent with one sidedness due either to differential dissipation or to Doppler boosting. There is no trend in either group for the jetted hot spot to be more distant, so if boosting is important the hot-spot separations must not reflect travel time differences from simultaneous ejecta. They might instead be determined by the history of the source, e.g. by a wandering or intermittent jet illuminating different parts of a lobe at different times. These trends imply that either (a) jet one sidedness has different causes in FR II sources with different fC or (b) the jets, but not the hot spots, are boosted in sources with fC < 0.05, while both are boosted if the core is strong. The relative brightnesses of hot spots are sensitive to linear resolution, however, so the trends must be checked with more uniform data.
Jets are surprisingly stable. They can extend for hundreds of
kiloparsecs or bend through
 90° (in C-shaped
"head-tails") without
disruption. Early analyses of the stability of confined cylindrical
jets to helical, fluting, and pinching perturbations analogous to the
Kelvin-Helmholtz instabilities of a vortex sheet
(15,
92,
93,
95,
110,
195)
suggested that jets are generally unstable to modes with
wavelengths of a few jet radii. The growth rates are less for
Mj > 1 and for
vj
90° (in C-shaped
"head-tails") without
disruption. Early analyses of the stability of confined cylindrical
jets to helical, fluting, and pinching perturbations analogous to the
Kelvin-Helmholtz instabilities of a vortex sheet
(15,
92,
93,
95,
110,
195)
suggested that jets are generally unstable to modes with
wavelengths of a few jet radii. The growth rates are less for
Mj > 1 and for
vj  c, but the stability of observed jets forces
re-examination of simplifying assumptions made in these analyses. The
stabilizing influence of a surface shear layer on modes with
wavelengths less than its scale depth was examined in
(92) and
(196),
and that of jet expansion on long-wavelength modes in
(111).
Within a thermally confined jet,
B|| may stabilize long-wavelength
pinching modes
(12,
92,
195).
The firehose instability can be inhibited by
sizable Bj and by linking the inertia of a plasma
cocoon around the jet to Bj
(12).
The stability of magnetically confined jets has yet to
be studied thoroughly, although first steps have been taken
(12,
16,
61).
Progress here is hampered by ignorance of basic MHD parameters in
jets: we know little about ion or electron temperatures, field
strengths, particle densities, and sound or Alfvén speeds, independent
of the assumption of equipartition. Currently favored models of jet
production from rotating disks or tori near supermassive objects
(e.g. 251)
may produce flows with net helicity. The influence of such
helicity on jet stability merits attention, as helicity can lead to
efficient generation of large-scale
Bj by turbulent amplification of small seed fields
(72).
c, but the stability of observed jets forces
re-examination of simplifying assumptions made in these analyses. The
stabilizing influence of a surface shear layer on modes with
wavelengths less than its scale depth was examined in
(92) and
(196),
and that of jet expansion on long-wavelength modes in
(111).
Within a thermally confined jet,
B|| may stabilize long-wavelength
pinching modes
(12,
92,
195).
The firehose instability can be inhibited by
sizable Bj and by linking the inertia of a plasma
cocoon around the jet to Bj
(12).
The stability of magnetically confined jets has yet to
be studied thoroughly, although first steps have been taken
(12,
16,
61).
Progress here is hampered by ignorance of basic MHD parameters in
jets: we know little about ion or electron temperatures, field
strengths, particle densities, and sound or Alfvén speeds, independent
of the assumption of equipartition. Currently favored models of jet
production from rotating disks or tori near supermassive objects
(e.g. 251)
may produce flows with net helicity. The influence of such
helicity on jet stability merits attention, as helicity can lead to
efficient generation of large-scale
Bj by turbulent amplification of small seed fields
(72).
Instabilities in real jets may grow algebraically, rather than exponentially. Exponential growth can be stopped in many ways - shock formation when the perturbation velocities become supersonic, shifting of the modes to longer wavelengths as their amplitudes grow, or saturation of the instabilities by in situ particle acceleration (15, 93, 94). Nondestructive instabilities might dominate the observed shapes and relative brightnesses of radio jets and lobes (15, 112, 286): algebraic growth of short-wavelength instabilities may help to keep jets bright (Section 4.3), long-wavelength helical modes to explain jet wiggling (Section 6.1.8), and pinching modes to form knots (Sections 4.1.4 and 4.3). Instability growth may also determine overall source sizes. MHD stability analyses including jet expansion, velocity and density gradients, and realistic Bj configurations and velocity profiles are needed; the analytical difficulties are great, and numerical simulations that do not legislate axisymmetry may be required.
"Unified" models seek to relate differences between sources with
weak and powerful radio cores solely to differences in viewing
angle. If the arguments in Section 6.2.1 indeed
support
 j >> 1 and
i
j >> 1 and
i  90° in the
jets of core-dominated sources, a randomly oriented sample
should contain
~ 2
90° in the
jets of core-dominated sources, a randomly oriented sample
should contain
~ 2 j2
unboosted sources for every boosted one if the
jets have narrow cone angles. For
<
j2
unboosted sources for every boosted one if the
jets have narrow cone angles. For
< j>
j>
 5
(169),
core-dominated
sources would number only a few percent of their parent population in
the plane of the sky, which may therefore be a well-known class of
object. Proposed parent populations for the core-dominated QSRs are
radio-quiet QSOs
(223)
and QSRs with lobe-dominated extended radio sources
(23,
169).
The latter proposal is not encouraged by the fact
that the lobe-dominated sources have weaker [Fe II] emission and
broader lines than core-dominated sources
(242,
281).
It is hard to
see how such differences in the line strengths could be produced by
the small aspect differences
(
5
(169),
core-dominated
sources would number only a few percent of their parent population in
the plane of the sky, which may therefore be a well-known class of
object. Proposed parent populations for the core-dominated QSRs are
radio-quiet QSOs
(223)
and QSRs with lobe-dominated extended radio sources
(23,
169).
The latter proposal is not encouraged by the fact
that the lobe-dominated sources have weaker [Fe II] emission and
broader lines than core-dominated sources
(242,
281).
It is hard to
see how such differences in the line strengths could be produced by
the small aspect differences
( i
i
 1 /
1 /
 j
radians) over which the Doppler-boosting factor varies markedly
(115).
Although the flux
density distribution of strong radio sources in optically selected QSO
samples conflicts with the unified models
(131, and references
therein), VLA studies of the Schmidt-Green QSO sample to a limiting
flux density of 250 µJy at 6cm are consistent with them over
most of
the flux density range. The "excess" of strong sources may be due to a
separate population of extended sources, most of whose emission is
presumably unbeamed (K. Kellermann et al., in preparation). As the
emission lines cannot be beamed, models that beam the optical
continuum luminosities of core-dominated QSRs predict the existence of
emission-line QSOs without nonthermal continua; these have not been
detected.
j
radians) over which the Doppler-boosting factor varies markedly
(115).
Although the flux
density distribution of strong radio sources in optically selected QSO
samples conflicts with the unified models
(131, and references
therein), VLA studies of the Schmidt-Green QSO sample to a limiting
flux density of 250 µJy at 6cm are consistent with them over
most of
the flux density range. The "excess" of strong sources may be due to a
separate population of extended sources, most of whose emission is
presumably unbeamed (K. Kellermann et al., in preparation). As the
emission lines cannot be beamed, models that beam the optical
continuum luminosities of core-dominated QSRs predict the existence of
emission-line QSOs without nonthermal continua; these have not been
detected.
About half of all core-dominated sources have detectable kiloparsec-scale secondary structure, which is generally one sided, as in Figure 5 (182, 185, 274). If the parent population is to be "radio quiet" (223) or to have normal two-sided lobes (169), both "unified models" must assert that most of this one-sided secondary structure is also boosted. The parent population of most core-dominated sources must then be a class of numerous weak extended radio sources with at least mildly relativistic kiloparsec-scale jets and relatively strong Fe lines.
As about half of all radio galaxies and nearly all QSRs have
detectable radio cores
(131,
and references therein), there must be a
mixture of boosted and unboosted contributions to the core
emission. Furthermore, some kiloparsec-scale jets emerging from weak
cores must have nonrelativistic velocities and intrinsic emission
asymmetries (Section 6.2.1), while some jets
emerging from powerful
cores may be relativistic (Section 6.2.3). It may
be that  core
core

 j >
j >
 h> in all
sources, while all three tend to increase with the actual
source power (measured by the luminosity of the most extended radio
features). The correlations between
Pcore and fC, the
occurrence rates
of jets (Section 2.3), their sidedness
(Section 3.1), their magnetic
field configuration (Section 3.2), and
the large-scale source
structure (FR class) might be assimilated in a broader unified model
as follows.
h> in all
sources, while all three tend to increase with the actual
source power (measured by the luminosity of the most extended radio
features). The correlations between
Pcore and fC, the
occurrence rates
of jets (Section 2.3), their sidedness
(Section 3.1), their magnetic
field configuration (Section 3.2), and
the large-scale source
structure (FR class) might be assimilated in a broader unified model
as follows.
The kiloparsec-scale jets in most weak sources have
vj << c, and so
appear two sided, with minor asymmetries that are either intrinsic or
the result of asymmetric internal dissipation of flow kinetic energy
to synchrotron radiation. They expand rapidly, so
B dominates over
B|| except at their bases. They have low thrusts and
so are readily bent, sometimes maintaining
B|| layers at their edges by shearing or
stretching as they bend. Low Mach numbers allow them to become
turbulent, to entrain material and thus to decelerate [all effects
that keep them well lit up (Section 4.3)],
and to terminate gently
without forming hot spots. These characteristics lead to FR I
morphology (Figure 1). Weak sources
with
dominates over
B|| except at their bases. They have low thrusts and
so are readily bent, sometimes maintaining
B|| layers at their edges by shearing or
stretching as they bend. Low Mach numbers allow them to become
turbulent, to entrain material and thus to decelerate [all effects
that keep them well lit up (Section 4.3)],
and to terminate gently
without forming hot spots. These characteristics lead to FR I
morphology (Figure 1). Weak sources
with  j =
j =
 h
h
 1 but
1 but
 core >> 1
would be strongly core dominated if oriented near the line of sight; their
extended low-brightness FR I structure would be detected only on maps
with high dynamic range. Such sources could be BL Lac objects with
very weak large-scale structure
(23,
37,
254).
There cannot, however, be large numbers of sources with
core >> 1
would be strongly core dominated if oriented near the line of sight; their
extended low-brightness FR I structure would be detected only on maps
with high dynamic range. Such sources could be BL Lac objects with
very weak large-scale structure
(23,
37,
254).
There cannot, however, be large numbers of sources with
 core >>
core >>
 j, or else we
would see many "coreless jets."
j, or else we
would see many "coreless jets."
The kiloparsec-scale jets in more powerful sources may have higher
vj. They may also have higher Mach numbers, leading to
narrower cone
angles where they are free and to prominent hot spots where they end.
They may be more stable, less turbulent, and thus dimmer relative to
their lobes, leading to FR II morphology. Higher vj
may lead, however,
to deeper boundary layers with the intergalactic medium, in which
B|| is maintained by shearing
(129,
208).
The combination of such shearing
and good collimation could make the jets that do stay lit up appear
B||- dominated
(Section 3.2) at low transverse
resolution. If vj -> c
in the more powerful sources, Doppler boosting may contribute to
correlations between jet detectability, fC, and
jet/hot-spot
symmetries (Section 6.3). The jets and some core
emission in powerful
sources near the plane of the sky would be beamed away from us,
producing "jetless" FR II sources with weak cores, as in the distant
3CR2 radio galaxies
(Section 2.2). Similar sources turned
toward us
would have strong cores and one-sided jets, as in the extended
3CR2
QSRs. The ~ 40 to 50% detection rate of jets in 3CR2 QSRs
requires, however, that only mild boosting
( j
j
 2) is usually
involved, and the lack of "coreless jets" again implies that
2) is usually
involved, and the lack of "coreless jets" again implies that
 core
core

 j in
general. Intrinsic asymmetries may therefore still be significant in
the powerful sources. There are weak relationships between
fC and
projected linear size, misalignments, and lobe separations among
extended QSRs
(130);
these relationships are consistent with some core
boosting in these sources.
j in
general. Intrinsic asymmetries may therefore still be significant in
the powerful sources. There are weak relationships between
fC and
projected linear size, misalignments, and lobe separations among
extended QSRs
(130);
these relationships are consistent with some core
boosting in these sources.
Such "unified models" of extragalactic radio sources may ultimately be judged by whether or not the optical and X-ray differences between different source types can be correlated with intrinsic source power and with indicators of the viewing angle.