Since the fuel for star formation is the interstellar gas, it is straightforward to assume that the star formation rate should be proportional to some power of the volumic gas density in galaxies, as done by Schmidt (1959). Following this assumption, Schmidt derived that this power should be around n = 2 (1) in the solar neighborhood. However, this local hypothesis has revealed very difficult to confirm, although there is of course some correlations between global gas density and star formation rate in a Galaxy. The difficulty is certainly related to the time delays and time-scales for star formation processes and subsequent feedback, and also to the fact that the gas can be stabilised by dynamical mechanisms, instead of forming stars.
2.1. Global statistical studies
So far, only global quantities have been correlated
with success, when the gas surface density is averaged
out over the whole galaxy, and the same for the star formation rate.
The star formation tracer can vary, from the
H
flux
for normal galaxies, to the Far Infrared luminosity L(FIR) for
starbursts, which are highly obscured
(Kennicutt 1998).
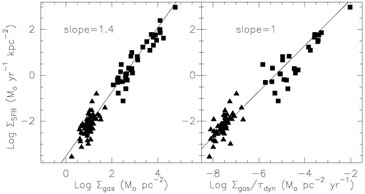
While the starbursts explore a wider range and dynamics of parameters, the relation between the global gas surface density and star formation rate (SFR) is the same for extreme and normal galaxies: it is possible to derive a "global" Schmidt law, with a power n = 1.4 (Kennicutt 1998).
|
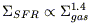
(cf figure 2). Another formulation works as well
|
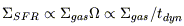
where 
is the angular
frequency in the galaxy, which is
inversely proportional to the dynamical time-scale tdyn.
Several justifications can be found a posteriori: if the star formation is locally due to the gravitational instability of the gas, this occurs on a free-fall time-scale, and the star-formation rate is:
|
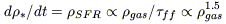
very close to the power n = 1.4; but the correlation is not observed locally. Globally, this applies also, if the star formation is due to the global gravitational instability of the gas disk, that occurs in a dynamical time-scale:
|
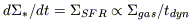
which accounts for the second formulation. Alternatively, star formation
could be triggered in marginally stable clouds, by the crossing of
spiral arms, and the frequency of arm crossing is
proportional to -
p
(Wyse & Silk 1989),
or roughly to far from
corotation (where the clouds never cross the arms).
This second formulation might also explain the Tully Fisher relation
(Silk, 1997;
Tan 2000),
since if 
SFR
gas
, then
|
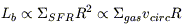
with vcirc2
R from the virial, and
provided that gas
* is
verified over the main spiral classes
(Roberts & Haynes
1994),
it can be deduced that Lb
vcirc3.
The numerical values found for the global Schmidt law correspond
to an SFR of 10% of gas per orbit transformed into stars,
at the outer edge typically for normal galaxies.
The much higher SFR in starbursts could be only a consequence of their much
higher surface density: indeed
gas is observed
to be 100 to 10 000 higher, and the star formation efficiencies (SFE)
about 6-40 times higher.
This higher efficiency can also be attributed to
smaller dynamical time-scales, since starbursts usually happen in
nuclear regions.
A starburst is obtained as soon as dynamical mechanisms have brought gas to the center; this can occur through gravity torques on dynamical time-scales. The gas infall must be sufficiently rapid to overcome the feedback processes, that will blow the gas out. These processes, such as supernovae explosions and violent stellar winds, occur on time-scales of 107 yr, the life-time of O-B stars. The latter is unchanged at any galactic radius, being intrinsic to stellar physics. Only in nuclei dynamical torques can bring the gas faster than these feedback mechanisms.
The global statistical studies appear to be slightly different for extreme
starbursts
(Taniguchi & Ohyama
1998).
The exponent of the global Schmidt law is more near n = 1, and
SFR
gas (cf also
Young et al 1986).
As for radial distribution, there is no correlation between
FIR and
gas.
It is the total gas amount of a galaxy that governs the infrared
luminosity L(FIR).
|
Figure 2. Relations between Star Formation
Rate (SFR) and gas surface densities, from
Kennicutt (1998).
Left: a global "Schmidt" law,
with a slope of n = 1.4 as the best fit. Right: linear relation
between SFR and gas over dynamical time (
|
2.2. Parameters governing the SFR
The difficulty is that there are many physical parameters determining the SFR and SFE in galaxy disks. Along the Hubble sequence, the star formation rate increases towards late-type, wich could be due to dynamical instability increasing with decreasing bulge-to-disk ratio. The SFE has been found to decrease with size (Young 1999). However, this could be due to a metallicity effect, since SFE is computed from the infrared to H2 ratio, SFE = L(FIR) / M(H2), itself derived from L(FIR) / L(CO), and L(CO) could lead to an underestimation of H2 in low-mass under-abundant galaxies.
The SFR also depends on environment, since galaxy interactions are one of the most widely recognized trigger of starbursts. Gravity torques are also essential for radial gas flows, and thus the bar phase or chronology might play a role, as well as the gas content.
The most essential physical parameters are :
c
(Quirk 1972,
Kennicutt 1989);
2,
that could imply a local Schmidt law. It is possible to account for
observations of SFR and SFE, by considering only collisions
(Scoville 2000,
Tan 2000);
Since all these phenomena play a role in the star formation, a global Schmidt law, averaged over the whole galaxy, is not sufficient to disentangle the relative importance of each process. In particular, local studies reveal that the gas density alone is not a sufficient parameter to predict SFR and SFE (cf gas concentrations without starbursts, Jogee & Kenney 2000).
It is tempting to test the stability of gaseous disks, with the Toomre
criterium Q (and its equivalent formulation as a critical gas density
c),
in order to explain the occurence of star formation in special regions
or galaxies. However in a dynamical time, gravitational instabilities
are able to heat a disk until the stability criterium is verified in
almost all disks, and external parameters are not included in the
criterium.
The main problem is that the criterium for gravitational instabilities is often undissociated from the criterium of star formation. But in reality, if gravitational instabilities are necessary for star formation, they are not sufficient. There are still some other parameters that are essential, controlling the onset of star formation in a gas medium that has formed self-gravitating structures, and those parameters are still to be sorted out and quantified to build a criterium for star formation:
1) Self-regulation
Gravitational instabilities are so important that disks are self-regulated to have the Toomre Q parameter of the order of 1. Indeed, as soon as Q falls below 1 because of gas dissipation, the disk becomes gravitationnally unstable: these instabilities have for immediate effect to increase the velocity dispersion, and heat the disk so that Q ~ O(1) again (e.g. Lin & Pringle 1987). But this self-gravitating process occurs even in the absence of star formation, so that Q ~ O(1) in any disk and cannot help to predict star formation.
For instance, in the outer parts of spiral disks, where it is obvious that there is no star formation at all, the HI gas is observed to be gravitationally unstable and form structures at all scales: there are spiral arms, giant clumps, and a mass spectrum of clouds (structures down to the smallest structure possible to see with the present 21cm beams). It is therefore likely that Q is also there of the order of 1, and the disk self-regulated. This occurs also inside some irregular galaxies, possessing a lot of gas, without star forming activity like N2915 (Bureau et al 1999). The gas has developped gravitational instabilities, spiral arms, etc..
2) Multi-phase gas and multi-components stability
Let us emphasize that Q and
c characterizing
the stability of disks, should be computed taking into account
all components, gas and stars, and in case of several gas components,
the total multi-phase medium. This is not possible analytically, since
the different components have not the same velocity dispersion, but an
empirical criterium has been proposed as:
|
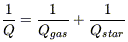
(Jog 1992).
Therefore, each component has a weight
/
in the stability.
When there is a large surface density of gas, the Qgas term
dominates, and it is justified to compute Q and
c taking
gas only into consideration. But as soon as the gas surface density
is depleted for some reason (for instance inside circum-nuclear rings),
or the gas is heated
(gas increases),
then the Qstar
term has to be taken into account, ensuring that the total Q is always
of the order of 1, over the whole disk (e.g.
Bottema 1993).
As for the gas velocity dispersion, when there exist
non-axisymmetric features, like spiral arms, bars, etc .. the corresponding
streaming motions have to be included in
gas (which does
not reduce to the local sound speed velocity of the order of 10km/s),
since it is precisely these streaming motions that are the consequences
of disk heating by spiral waves and gravitational instabilities.
3) Spatial averaging scale
A problem in estimating Q and
c is also the
scale at which they
are averaged, and the results can change completely according to the
spatial resolution of the observations.
We know that the interstellar medium is fractal and possess structures
at all scales,
from 100 pc to ~ 10 AU. The gas surface density increases towards
small scales, by about 1-2 orders of magnitude; the critical surface density
might be reached or not, according to the spatial scale of averaging
(Klessen 1997;
Wada & Norman 1999,
2001;
Semelin & Combes 2000;
Huber & Pfenniger
2001).
4) Uncertainty on the H2 gas density
The biggest uncertainty in computing the gas surface density is
the CO to N(H2) conversion ratio. This ratio can vary within
a factor 2 or 10, according to metallicity, CO excitation, temperature,
density, etc ..
(Rubio et al 1993,
Taylor et al 1998,
Combes 2000),
and since Q ~ O(1) in galaxy disks
anyway, it is quite impossible to ascertain that Q is larger or smaller
than 1 if such systematic uncertainties are
attributed to the gas density. Due to the latter,
it is likely that systematics will find
gas <
c
for non-star forming regions, where the CO is not excited (or the
metallicity not enough), and
gas >
c for starbursts
(12C is a
primary element, and the abundance of CO is enhanced in starbursts).
5) Intermittency
Star formation can be inhibited or triggered by other phenomena, such as
supernovae, stellar winds, external or internal wave triggers and this does
not enter the Q and
c estimations. In
a nuclear disk, simulations by
Wada & Norman (2001),
the density undergoes phases of episodic
and recurrent star formation (of the order of ~ 10 Myr periodicity),
and the estimation of
c are the same
for periods with and
without star formation. Here is introduced a hidden parameter, which
is the past history of star formation. A galactic disk region might be
quiescent, only in between two star formation phases for instance.
In conclusion, gravitational instabilities ensure that all spiral disks have Q ~ O(1) at all radii: the gas component is structured in clouds that are marginally stable. Only transiently the disk can be brought out of equilibrium. Only a sudden trigger is necessary to start a starburst, and these are difficult to recognize. This could be a sudden radial gas flow due to a bar, or the tidal action of a companion, that strengthens or creates a bar, that will bring gas to the nucleus, when the dynamical time-scale is short.
To have a starburst, gas must be gathered in a very short time-scale, smaller than ~ 107 yr, shorter than the onset of feedback from the first OB stars formed, through supernovae explosions and stellar winds, before the starburst can blow the gas out. In nuclei, the dynamical time-scale is shorter, while the feedback time-scale is constant all over the disk (being intrinsic to the life-time of OB stars). That might explain why starbursts are always more conspicuous in nuclei.
The original Schmidt law is a local one, and involves the volumic density
. At this stage,
one should consider that the surface density in inner and outer
parts of the galaxies have not the same weight for gravitational
instabilities, because of the flaring of gas and star densities towards
the outer parts.
It was found, with IRAS fluxes as a tracer of star formation, that barred galaxies were more frequently starbursting (Hawarden et al. 1986), and had also more radio-continuum central emission, attributed to star formation (Puxley et al. 1988). From a statistical sample of more than 200 starbursts and normal galaxies, Arsenault (1989) found a much larger frequency of barred and ringed types among the starbursts, suggesting that active formation of stars in the nuclei of spirals is linked to the perturbation of bars and gravity torques.
But such a correlation is not without any controversy: Pompea & Rieke (1990) do not find that strong bars appear an absolute requirement for high infrared luminosity in isolated galaxies. Markarian starbursting galaxies are less barred than a sample of normal galaxies (Coziol et al. 2000).
At least the molecular gas appears much more concentrated in barred galaxies (Sakamoto et al 1999), which is expected form gravity torques. This gas concentration should trigger nuclear starbursts, according to the Schmidt law.
As for nuclear activity itself, the correlation between the presence
of bars and AGN activity is presently unclear, as described already in this
conference.
Peletier et al (1999)
and Knapen et al (2000)
have shown that Seyferts have more bars than normal galaxies
(results at 2.5).
Seyferts have curiously a lower fraction of strong bars
(Shlosman et al 2000),
perhaps pointing toward
the destruction of bars by massive black holes.
Besides, Seyferts have more outer rings, by a factor 3 or 4
(Hunt & Malkan 1999).
Since the outer rings are the vestiges of
the action of bars, this supports the scenario of bar destruction by
central gas accretion and massive black holes.
An interesting feature recently discovered in stellar kinematics of star-forming galaxies with an active nucleus, is the drop in velocity dispersion in the central kpc. This was found thanks to ISAAC on the VLT (Emsellem et al 2001, and this conference). This drop is unexpected, especially since the dispersion should increase towards the massive black hole. But the phenomenon can be transient, and due to kinematically cold stars just formed from the gas in the nuclear disk fueled by the bar torques.
As for numerical simulations, starbursts are easily reproduced, in particular triggered by galaxy interactions and mergers. The star-formation is due to radial gas flows, driven by the bars formed in the interaction (e.g. Mihos & Hernquist 1994, 1996; Bekki 1999). The bar is thus central to the starburst. The presence of a bulge, which has a stabilising influence on disks against bar formation, is determinant in the occurence of the starburst. In galaxies with a large bulge-to-disk ratio, the intense starburst has to wait the merging, and the final gas infall, while galaxies without large bulges undergo repetitive starbursts.
Other dynamical perturbations, like lopsidedness and m = 1 waves are also triggering starbursts: in this case, star formation is mainly in the disk, and not boosted in the nucleus (Rudnick et al 2000).
1 Schmidt compared the scale-height of the galactic plane in gas and young stars to derive this power, and found a high value because the molecular hydrogen distribution was not known at that time Back.
dyn) ratio. Normal
galaxies are the
triangles, while starburst galaxies are the squares.