Global versus Nuclear Starbursts

3. LARGE GAS COMPLEXES AND STELLAR CLUSTERS

Due to the large gas surface density in nuclear starbursts, the critical length for self-gravity in the disk center (the scale with the largest growth rate) is also very large:

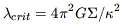
where Sigma ~ Sigma _gas, since the gas is dominating there. The corresponding self-gravitating mass is lambda ² Sigma , or propto Sigma ³. Figure 3 gives orders of magnitude for these values, typical sizes and masses 200 pc, 10⁹ M.

Figure 3. Left Critical length scale for self-gravitation lambda _crit (solid line) as a function of radius, together with the corresponding mass of structures (dashed, right scale), for an exponential gas surface density, as represented in dotted line (maximum Sigma ₀ = 5 × 10³ M/pc² or 3 × 10²³ H₂ cm^-2). Right The critical length scale has been computed for this rotation curve, and corresponding frequencies kappa , and Omega - kappa / 2.

These super complexes will collapse, and may form super star clusters, if another factor is tuned, the time-scale before feedback effects come into play, and regulate the star formation. The collapse of gas must be sudden enough (in < 10 Myr), so that OB stars and SN cannot limit the process. This means that the free-fall time is short enough, and therefore that the volumic density is larger than 2 M / pc³. This is indeed verified for the typical masses and sizes determined above, but not for usual giant molecular clouds.

Another point of view to see the formation of these large complexes, is to introduce the velocity dispersion (Elmegreen et al. 1993). In interacting and merging galaxies, one characteristic is that the tidal perturbations have increased velocity dispersion above that of a quiescent disk, and the corresponding pressure stabilises locally the gas up to a larger Jeans length. The complexes that form are then bigger.

The largest growth rate for instabilities in the disk occurs at the scale lambda _crit considered above, which is also equal to the Jeans length:

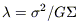
since the Toomre parameter Q ~ sigma kappa / G Sigma ~ 1. In fact, the kinetic pressure stabilises all scales below Jeans length, and the galactic rotation stabilises all scales above lambda _crit, the equality between the two ensuring the disk stability. If the disk is slightly out of equilibrium, it is those common scales that are unstable more quickly.

With this second formulation, the mass of the complexes are proportional to sigma ⁴ / Sigma , and grow at a rate tau _ff = sigma / Sigma showing the large importance of velocity dispersion.

Super Star Clusters (SSC) are young star clusters of extraordinary luminosity and compactness. They are one of the dominant modes of star formation in starbursts, and they are thought to be a formation mechanism for globular clusters. A major breakthrough from HST has been to show that globular clusters form still at the present time, through starbursts (e.g. Schweizer 2001). The question has been raised of the SSC contribution to the total luminosity: it appears only moderate in ULIRGs (Surace et al 1998). In Arp 220 for example (Shioya et al 2001), there are three conspicuous nuclear SSC (galactic radius < 0.5kpc), which correspond to about 0.2 L_tot (they are heavily obscured > 10 mag). The disk SSC (0.5 < radius < 2.5 kpc), of lower luminosity, represent a negligible contribution. SSC also form in starbursting dwarfs, with properties quite similar to larger interacting/merging galaxies (e.g Telles 2001). In these systems, they could represent a significant part of the luminosity. Their formation is thought to be triggered by the high pressure experienced by the gas complexes in a starburst environment.