2. METHODS OF ABUNDANCE DETERMINATION

2.1. The "Conventional" (Direct) Method

2.1.1. Basic Steps. In this review, I will emphasize the techniques of abundance determinations and their advantages and pitfalls, rather than the latest set of results, in the hope that a critical discussion of methods will have greater longevity than a set of numbers subject to future revision. The standard method of deriving nebular abundances from emission lines is explained in great detail in references on the physics of gaseous nebulae (Aller 1984; Osterbrock 1989). The procedure is summarized by the following flow-chart.

Observed Emission Line Intensities
 |               {Correction for Extinction using
 V               Hydrogen Recombination Decrement}


Reddening-Corrected Line Intensities
 |               {Diagnostic Line Ratios, e.g.
 V               [O III] for Te, [S II] for ne}


Local Physical Conditions (ne, Te)
 |               {Ionic Level Populations and
 V               Calculated Line Emissivities}


Ionic Abundance Ratios (O+ / H+, O++ /
 H+, etc.) 
 |               {Correction for Unobserved Ions}
 V


Elemental Abundance Ratios (O/H, etc.)

2.1.2. Choice Of T_e. A key species for nearly all nebular abundance determinations is the O⁺⁺ ion. Figure 1 shows the energy-level structure and major transitions for the ground configuration. The intensity ratio [O III] 4363Å / 5007Å (and/or 4959Å) has long been the chief diagnostic of the gas temperature in nebulae. Recent improvements in the calculated collision strengths (Mendoza 1983; Osterbrock 1989) cause systematic revisions by up to factors of two in the derived abundances (e.g. Zamorano and Rego 1985).

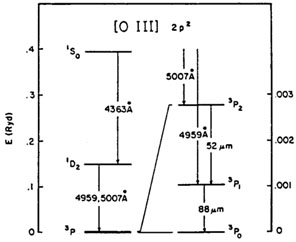
Figure 1. The energy-level diagram for the ground configuration of the O++ion, with the most important transitions indicated, from Dinerstein, Lester, and Werner (1985).

A more subtle effect arises because the derived temperature is necessarily weighted by the temperature dependences of the lines. Both 4363Å, and to a lesser and different degree 5007Å, are more strongly emitted by hotter gas. For a non-isothermal nebula, this results in a tendency to overestimate T_e and underestimate O⁺⁺/H⁺. A procedure for correcting for these effects was developed by Peimbert (1967; also see Rubin 1969), who characterized the temperature distribution in terms of a mean value T₀ and an rms "fluctuation" parameter t² which serves as an indicator of the amplitude of the temperature spread within the region; these variations may be either microscopic or macroscopic. In principle, measurement of two line ratios with known functional dependences on temperature yields a simultaneous solution for both T₀ and t², and allows one to correct the line emissivities used to derive ionic abundances. The magnitude of these corrections for reasonable values, t² = .00, .035, and .055, can be seen in Table 10 of Peimbert and Torres-Peimbert's study of Orion (1977). For N, O, Ne, and S, the elemental abundances increase by roughly .25 and .45 dex respectively (factors of about 2 and 3) if t² = .035 or .055. The corrections to ionic abundance ratios such as C/O and N/O are substantially smaller (Zuckerman and Aller 1986). It is notable that the abundances relative to hydrogen derived assuming t² = .00 are systematically lower than stellar abundances, while a modest nonzero t² brings them into agreement with the solar and stellar abundance scale. In principle, values for t² are best determined from two temperature-diagnostic line ratios which arise from the same volume, e.g. from the same ion. Such a solution has been done recently for planetary nebulae using the far-infrared lines of [O III] in combination with the optical lines (Dinerstein, Lester, and Werner 1985), who find evidence for non-zero values. Nevertheless, the correction for non-isothermality is rarely made for extragalactic H II regions, primarily because it is difficult to measure the necessary line ratios.

2.1.3. Correction for Unobserved Ions. Perhaps the most difficult step in the abundance solution is to correct for ions which may be common in the nebulae but do not give rise to conveniently observable emission lines. The magnitude of this correction varies greatly from element to element. Oxygen is the best case, since there are intrinsically strong optical lines for the two generally most abundant ions, O⁺ and O⁺⁺. A set of formulae defining "ionization correction factors" (i_cf's) which convert ionic into elemental abundance ratios was introduced by Peimbert and Costero (1969). These formulae are based on near-coincidences between the ionization potentials (I.P.'s) of various ions, and assume that the fractional ionic populations are the same as those of ions with similar I.P.'s. For example, the I.P. for N⁺ is 29.6 eV, while that of O⁺ is 35.1 eV, so one assumes that (N/H) = (N⁺ / H⁺) × i_cf(N) = (N⁺ / H⁺) × (O⁺ + O⁺⁺) / O⁺, or (N/O) = (N⁺ / O⁺). Likewise, the ionization potentials of O⁺ and S⁺⁺ are similar, suggesting a parallel correction formula for S⁺³, These formulae are still often used, although it is clear that the I.P.'s do not tell the whole story; in some cases other factors, such as recombination coefficients and charge-exchange reactions, can significantly change the ionization balance (for sulfur, for example: see Natta, Panagia, and Preite-Martinez 1980; Dinerstein 1980; Garnett 1989a, b).

2.2. Nebular Models

Another approach to interpreting nebular spectra is to construct models of the nebular ionization and thermal structure. One can either tailor a model to a specific region and optimize the match to the observed line intensities (e.g. Dinerstein and Shields 1986), or utilize grids of models covering an appropriate range of nebular parameters (e.g. Stasinska 1978; Dufour et al. 1980; Mathis 1982; Evans and Dopita 1985). In the latter method, ionic abundances are basically derived using the direct method, but the models are used to estimate the electron temperatures and ionization correction factors for individual ions.

The ingredients of a model are: (1) T_*, the effective temperature of the ionizing stars (or, more generally, the spectral energy distribution of the ionizing radiation, taken from model stellar atmospheres); (2) a set of elemental abundances such as (O/H), which determine the local cooling efficiency, and hence the gas temperature; and (3) the gas density, often parameterized in terms of the "ionization parameter". The ionization parameter is given by U = Q(H⁰) / [4 r²_S nc] [Q(H⁰)nf²]^1/3, where Q(H⁰) is the number of H-ionizing photons, r_S is the Strömgren radius, n is the gas density within the clumps, and f is the volume filling factor of the clumps (e.g. Shields 1986; note that other authors may use slightly different definitions of U). The ionization parameter is essentially the local ratio of Lyman-continuum photons to gas density, which determines the degree of ionization at any particular location within the nebula (a point stressed by Mathis 1985). The abundances of the other elements are often assumed to scale with oxygen, which is itself the main driver of the gas cooling, through its strong emission lines. As the abundances vary, the nebular structure and emergent spectrum may change drastically (e.g. Stasinska 1980). A further refinement is to allow for the fact that presumably the abundances in the atmospheres of the ionizing stars are the same as those in the nebular gas (Balick and Sneden 1976; Shields and Searle 1978; Skillman 1989).

Most models, especially those designed for extragalactic H II regions, assume a spherical geometry but allow for clumping of the gas (with filling factors of .01 - .001 as discussed above). Some workers have suggested that dust within the nebula softens the ionizing radiation field (Sarazin 1977; Herter, Helfer, and Pipher 1983), but others find that the effect of dust is unimportant (Mathis 1986); the result depends the assumed grain optical properties, which are poorly known.

2.3. "Bright-Line" Methods

Many extragalactic nebulae are too faint to permit measurement of weak lines, such as [O III] 4363Å, which are needed for the analysis methods described above. In these cases, it is still possible to obtain estimates of the nebular abundances, using intensity ratios among the handful of brightest ionic emission lines. This is referred to as the "empirical" or "semi-empirical" approach, or, more descriptively, as the "bright-line" method. The physical basis lies primarily in the energy-level structure of the main coolant for most H II regions, the O⁺⁺ ion. The rate of energy lost via a collisionally excited line is proportional to the factor exp(- / kT), where is the energy of the level from which the line arises. The exponential term varies steeply near T_e = 10⁴ K, a typical value for H II regions, for the strong optical lines 4959, 5007Å. However, it is nearly constant for the 52 and 88 µm lines which arise from fine structure in the ³P ground term (see Figure 1). This leads to a behavior which may initially seem counterintuitive: as O/H decreases, the cooling in all of the [O III] lines drops and T_e rises; as a result, 4959 and 5007Å brighten dramatically. On the other hand, as O/H increases, T_e drops and the optical lines weaken greatly; in this case, most of the cooling occurs through the infrared lines. This basic mechanism was recognized by Searle (1971) and further developed by Shields (1974). The other optical lines also have fairly strong temperature dependences, but in some cases, such as [O II] 3727Å, the ion does not have fine-structure in the ground term providing an alternate outlet for radiative energy losses. On the other hand, the (generally) most abundant ion of sulfur, S⁺⁺, has an energy-level structure similar to that of O⁺⁺, with strong lines at 9069, 9532Å analogous to 4959, 5007Å, and infrared lines at 18, 35 µm.

In H II regions where both can be measured directly, the electron temperature does correlate with O/H (see, for example, Figure 1 in Pagel 1986). The line ratio ([O II] 3727Å+ [O III] 4959, 5007Å) / H was calibrated and employed as an abundance indicator for extragalactic H II regions by Pagel et al. (1979), and has since been recalibrated several times (e.g. Edmunds and Pagel 1984; Dopita and Evans 1986). Permutations of these line ratios and combinations with lines of [N II], [S II], and [S III] have been considered by McCall, Rybski, and Shields (1985), Mathis (1985), and others. It is clearly preferable to use the ratio ([O II]+[O III]) / H rather than [O III] / H, although the latter is easy to measure because the lines are adjacent in wavelength (e.g. Zaritsky, Elston, and Hill 1989), because [O III] / H depends on the degree of ionization. Unfortunately, once the abundance approaches solar, the radiative cooling becomes so efficient that the weak, highly temperature sensitive line [O III] 4363Å is essentially unobservable (in distant H II regions). Thus, the high-abundance end of this relation is intrinsically difficult to calibrate, and relies heavily on nebular models. This calibration is one of the main sources of disagreement in the abundance values derived by different authors.

It is also important to recognize that this simple inverse relation between abundance and [O III] line strengths breaks down at very low metallicities, where 4959, 5007Å weaken in proportion to the O/H abundance because this ion no longer dominates the cooling. This effect produces another "branch" in the ([O II]+[O III]) / H diagram, for which the line strengths vary in direct proportion to abundance. Since the "turn-around" point falls near (O/H) = 10^-4, the most metal-poor (and hence, often the most interesting!) H II regions fall in a part of the diagram where the line strength-abundance relationship is double-valued. This fact must be kept in mind when applying the bright-line method to samples of nebulae which might include very low metallicity regions.