The first step in the analysis of emission line strengths from nebulae is generally the derivation of physical parameters that characterize the local conditions in the gas, primarily density and temperature (see the synopsis of the standard or "conventional" analysis of H II regions, in Dinerstein 1990). This is as true for infrared lines as for optical/uv lines, and the specific methods used with infrared lines are essentially analogs of techniques developed for optical/uv lines.
Determination of the extinction towards the line-emitting material is a
prerequisite to
the derivation of other properties, since further analysis requires
knowledge of the true
line intensities, corrected for extinction. The usual approach is to
measure the intensity
ratios among lines whose intrinsic relative strengths are considered
known. Discrepancies
are ascribed to extinction, assumed to follow a particular law
A(
), and a best fit is found
for the overall scaling factor, usually characterized by
AV or sometimes AK (i.e.,
Mathis 1990).
The most commonly used set of line ratios is the recombination spectrum
of H I; this is called the hydrogen decrement method. In the
optical, one uses the Balmer lines
(e.g., H
/
H
,
H
/
H), whose relative intensities
in the absence of extinction are known
to high accuracy and have little dependence on temperature or density
(Osterbrock 1989,
ch. 4.2). The main transitions used in the infrared are the Paschen and
Brackett series,
which extend out to 4.05 µm (Br
). These lines are used to
determine extinctions
to H II regions in our own Galaxy, and in other galaxies (e.g.,
Lester et al. 1990).
A couple of caveats should be kept in mind, however. First, where the
geometry is complex
and the observations integrate over material with a range of
AV values, the effective
extinction law may have a form quite different from the standard one,
and may have to be
determined empirically by sampling lines at various wavelengths and
interpolating (i.e.,
Lester, Dinerstein, &
Rank 1979).
Second, there are situations, such as high densities
and high optical depths, where the intrinsic recombination decrement
deviates strongly
from the classic "Case B" values. Examples of the latter range from the
"line excess" problem in young stellar objects
(Thompson 1982;
Natta et al. 1988),
to broad lines in active galactic nuclei
(Kawara, Nishida, &
Phillips 1989;
Goodrich 1990).
When H I recombination lines are not available, one can use pairs or sets of lines with different wavelengths that arise from the same upper level of any species. An early example of this method was a comparison the strengths of [S II] lines near 1 µm with others near 4000 Å (Fig. 1) to determine the extinction towards the metal-rich knots in the Cas A supernova remnant (Searle 1971); these knots are composed entirely of heavy elements and contain no H or He at all. To determine extinctions towards regions where hydrogen is molecular, it is common to use H2 quadrupole lines from common upper levels; applications include the shocked gas in Orion (e.g., Geballe et al. 1986) and the evolved bipolar nebula GL 618 (Latter et al. 1992). The rich energy level structure of Fe II (Nussbaumer & Storey 1988) provides a multitude of line ratios to use in partially ionized regions such supernova remnants (see Fig. 1).
|
Figure 1. Energy levels of Fe II & S II. (From Oliva, Moorwood, & Danziger 1991) |
The honorees of this conference were among the pioneers in using optical line intensity ratios to deduce densities in ionized nebulae (Seaton & Osterbrock 1957; updated in Fig. 5 of Osterbrock 1988). Intensity ratios of pairs of infrared lines can similarly be used to infer gas densities. A comprehensive discussion of infrared density indicators is given by Rubin (1989). The critical densities of the infrared lines fall mostly in the range 102 cm-3 < ncrit < 106 cm-3, with a general tendency of the longer-wavelength lines to have lower values than shorter-wavelength lines because of their lower A values (equation 1.2). For example, log ncrit([O III] 51.8, 88.4 µm) (3.5, 2.7), while log ncrit([N II] 122, 204 µm) = (2.4, 1.6). On the other hand, the critical densities of [S III] 18.7, 33.5 µm are higher than those of some optical lines (see Fig. 2). These three pairs of lines have been used extensively to study obscured Galactic H II regions (e.g., Moorwood et al. 1980; Colgan et al. 1993). Ratios of infrared to optical lines can also be used as density indicators (e.g., Keenan & Conlon 1993).
|
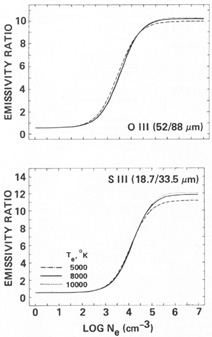
Figure 2. [O III], [S III] lines as ne diagnostics. (From Rubin 1989) |
In partially ionized regions where the gas is heated by shocks and/or by photoelectrons donated by species such as C+, Si+ and Fe+, local gas densities can be derived from ratios of [Fe II] lines. This species provides a multitude of strong emission lines in the infrared, particularly between 1.25 µm and 1.9 µm, from which density-sensitive ratios can be formed (Nussbaumer & Storey 1988). Most of these [Fe II] ratios are useful density indicators at relatively high densities, 104 < n < 105.5 cm-3 (e.g., Oliva, Moorwood, & Danziger 1989).
Studies that have measured densities from more than one pair of infrared lines often find that different indicators yield different nominal values of ne. This should not come as a surprise. It behooves us to bear in mind the complexity of real nebulae and the limitations of diagnostics:
"It must always be remembered that mean temperatures and densities derived from these diagnostic ratios are complicated averages over the structure of the nebula, weighted by the emission processes themselves. Thus the mean temperature is weighted toward high temperature, where the collisionally excited emission lines are all strongest, and the mean density is weighted toward the critical densities, where the emission 1s most efficient."
(Osterbrock 1988, p. 419). For ratios involving infrared lines only, temperature effects are minimal, but density is an important consideration. Nebulae are almost inevitably inhomogeneous, probably both on large and small scales, and diagnostics from lines with different critical densities will be biased accordingly. The effects of such biases can propagate further in the analysis. If the "wrong" (single-value) density is inferred, then the wrong emissivity will be used in the subsequent calculations, and an incorrect abundance will be derived. Rubin (1989) examined the effects of such "density bias" on ionic ratios, for several representative cases of inhomogeneous nebulae. He found that the errors in the derived abundance vary widely for different sets of lines, ranging from negligible (e.g., < 10% for N++/O++) to significant (> 50% for several other ratios under reasonable conditions); his analysis also included many optical/uv line diagnostics.
2.3. Electron Temperature (Te)
Electron temperatures (Te) of ionized nebulae can be
determined from intensity ratios
of collisionally excited lines from levels of widely separated
energies. The pre-eminent
optical line indicator for Te is the ratio of [O III]
4363 Å to one or both of the stronger
[O III] lines at 4959, 5007 Å (e.g.,
Osterbrock 1989,
Fig. 5.1;
Dinerstein 1990).
As pointed out in Section 1, infrared
fine-structure lines are relatively insensitive to
Te.
Thus, by themselves they are not useful for measuring
Te in typical hot, ionized nebulae;
however, one can construct Te diagnostics by comparing
infrared lines from low-lying
levels with optical/uv lines from higher-excitation levels. This can
provide a means to
derive Te values for regions that lack optical/uv
Te diagnostics. For example, [Ne V]
24.3 µm can be combined with [Ne V] 3426Å, and [O II} 25.9
µm similarly with far-uv
lines, to infer Te for the high-ionization zones of
planetary nebulae
(Shure et al. 1983a,
b;
Rowlands et
al. 1989).
In regions that do not produce optical/uv emission lines,
infrared line ratios can be used as temperature indicators in particular
regimes, e.g., [O I] 145/63 µm at T
500 K. However, because infrared
lines are strongly affected by
collisions at relatively low densities, their dependences on n
and T are often difficult to
separate. It may be necessary to measure at least two line ratios from
one ion in order to derive meaningful constraints on T
(Keenan, Burke, &
Aggarwal 1991).
In some cases it is necessary to combine lines from more than one
species and assume a value for their
relative abundances. For example, in photodissociation regions, [O I]
63, 145 µm and
[C II] 157 µm can be used together to constrain n and
T, at least in certain regimes
(Fig. 3, from
Watson 1985;
also Tielens &
Hollenbach 1985).
|
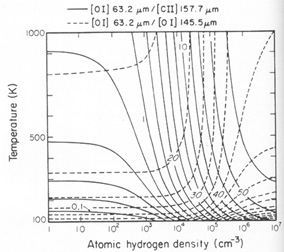
Figure 3. Mapping of the infrared [C II], [O I] line ratios to n and T. (From Watson 1985). |
There is no reason to expect that real nebulae are isothermal. As was
the case for
density, observations will include emission from material at a range of
temperatures,
particularly if made with large apertures. The spread in temperatures is
likely to be
modest ( 30%) compared to density
inhomogeneities, which could cover several orders
of magnitude. However, for optical/uv lines, with their exponential
emissivity dependence
on Te, even modest Te variations
produce enormous changes in line strengths and
inferred parameters. A formalism for characterizing the temperature
distribution in non-isothermal nebulae was introduced by
Peimbert (1967),
who defined a mean temperature
T0 and an rms "temperature fluctuation parameter"
t2. These parameters can be related
to, and therefore measured by, intensity ratios of lines with different
temperature dependences (i.e.,
Peimbert & Costero
1969).
If the spread in Te is large, the use of a single
Te value (determined from the standard diagnostics) to
determine ionic abundances can yield inaccurate results. A spread of
just a few percent can lead to abundance errors of
a factor of two or worse, for very temperature-sensitive lines!
The rich infrared-optical [O III] spectrum offers a particularly attractive opportunity to constrain and characterize the temperature properties of nebulae. The ground 3P term gives rise to the strong far-infrared lines at 52 and 88 µm that have already been discussed as density indicators, whereas the higher levels produce the traditional optical [O III] temperature diagnostic (Fig. 4). By combining observations of a single far-infrared line (e.g., 88 µm) with two optical lines, Dinerstein (1983) showed that it was possible to solve simultaneously for ne and Te from a single ion. In Dinerstein, Lester, & Werner (1985, hereafter DLW), both far-infrared [O III] lines were compared with 5007 Å; the mapping of this ratio in the (ne, Te) plane is shown in Fig. 5. The latter technique has the advantage of providing a determination of Te that is independent of the 4363/5007 Å line ratio, and is less weighted or "biased" by small amounts of high-temperature gas than the optical ratio. Indeed, if one can measure four [O III] lines in a particular nebula and therefore construct three diagnostic line ratios, it should be possible to extract a measure of the inhomogeneity of the gas in addition to "mean" values of ne and Te. As shown in DLW (Appendix), using Peimbert's (1967) formalism,
| (2.3) |
making it (in principle) straightforward to solve for values of both T0 and t2. The accuracy of this method, however, depends critically on one's ability to calibrate the absolute far-infrared fluxes correctly, since ratios are taken relative to optical line fluxes measured with completely different instrumentation and flux standards. DLW concluded that there was evidence for significant non-zero values of t2 in four observed planetary nebulae, with an average value of about .06. Compensation for this degree of inhomogeneity would elevate the O/H abundance by nearly a factor of two. These values of t2 are only slightly higher than recent values derived for several galactic H II regions from various optical indicators (Peimbert 1993 and references therein). However, new and better-calibrated measurements of the far-infrared lines in NGC 6543, formerly found by DLW to have t2 > 0.1, suggest that the actual value is smaller (Dinerstein et al. 1995). The promise of this method, and implications for the nebular oxygen abundances, await a larger set of accurately calibrated far-infrared line fluxes for optically well-studied nebulae, which are likely to become available in the next few years, from airborne studies and from new infrared space observatories.
|
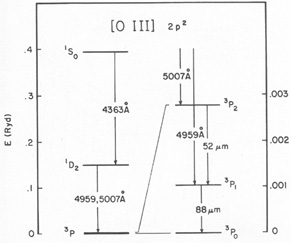
Figure 4. Energy level diagram for [O III]. (From Dinerstein, Lester, & Werner 1985.) |
|
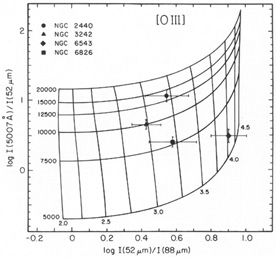
Figure 5. Infrared/optical [O III] diagnostics. (From Dinerstein, Lester, & Werner 1985.) |