2. The Conceptual Framework

The engine that drives the observed outflows in starbursts is the mechanical energy supplied by massive stars in the form of supernovae and stellar winds (Leitherer & Heckman 1995). For typical starburst parameters, the rate of supply of mechanical energy is of-order 1% of the bolometric luminosity of the starburst and typically 10 to 20% of the Lyman continuum luminosity.

The dynamical evolution of a starburst-driven outflow has been extensively discussed (e.g. Chevalier & Clegg 1985; Suchkov et al. 1994; Wang 1995; Tenorio-Tagle & Munzo-Tunon 1998; Strickland & Stevens 2000). Briefly, the deposition of mechanical energy by supernovae and stellar winds results in an over-pressured cavity of hot gas inside the starburst. The temperature of this hot gas is given by:

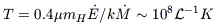
for a mass (kinetic energy) deposition rate of (). The ``mass-loading'' term represents the ratio of the total mass of gas that is heated to the mass that is directly ejected by supernovae and stellar winds (e.g. 1).

This hot gas will expand, sweep up ambient material and thus develop a bubble-like structure. The predicted expansion speed of the outer wall of such an adiabatic wind-blown superbubble is of-order 10² km s^-1:

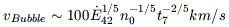
for a bubble driven into an ambient medium with nucleon density n₀ (cm^-3) by mechanical energy deposited at a rate (units of 10⁴² erg s^-1) for a time t₇ (units of 10⁷ years).

If the ambient medium is stratified (like a disk), the superbubble will expand most rapidly in the direction of the vertical pressure gradient. After the superbubble size reaches several disk vertical scale heights, the expansion will accelerate, and it is believed that Raleigh-Taylor instabilities will then lead to the fragmentation of the bubble's outer wall (e.g. MacLow, McCray, & Norman 1989). This allows the hot gas to "blow out" of the disk and into the galactic halo in the form of a weakly collimated bipolar outflow (i.e. the flow makes a transition from a superbubble to a superwind). The terminal velocity of this hot wind is expected to be in the range of one-to-a-few thousand km s^-1:

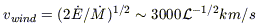
The wind will carry entrained interstellar material out of the galactic disk and into the halo, and will also interact with ambient halo clouds (e.g. Suchkov et al. 1994; Strickland & Stevens 2000). This interstellar material will be accelerated by the wind`s ram pressure to velocities of few hundred km s^-1:

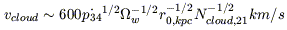
for a cloud with a column density N_{cloud, 21} (units of 10²¹ cm^-2) that - starting at an initial radius of r₀ (kpc) - is accelerated by a wind that carries a total momentum flux of (units of 10³⁴ dynes) into a solid angle (steradian).