


While it is relatively straightforward to demonstrate that
a superwind is present, it is more difficult to robustly calculate the
rates at which mass, metals, and energy are being transported out by
the wind. Several different types of data can be used, each with its
own limitations and required set of assumptions.
X-Ray Emission: X-ray imaging spectroscopy yields the superwind's
"emission integral".
Presuming that the X-ray spectra
are fit with the correct model for the hot gas it follows that
the mass and energy of the X-ray gas scale as follows:
MX ![]() (LXf )1/2 and
EX
(LXf )1/2 and
EX ![]() (LXf )1/2TX(1 +
(LXf )1/2TX(1 + ![]() 2). Here
f is the volume-filling-factor of the X-ray gas and
2). Here
f is the volume-filling-factor of the X-ray gas and
![]() is its Mach number. Numerical hydrodynamical simulations
of superwinds suggest that
is its Mach number. Numerical hydrodynamical simulations
of superwinds suggest that
![]() 2 = 2 to 3
(Strickland & Stevens
2000).
The associated outflow rates (
2 = 2 to 3
(Strickland & Stevens
2000).
The associated outflow rates (![]() and
and ![]() )
can then be estimated by dividing
MX and EX by the crossing time of
the observed region:
t
)
can then be estimated by dividing
MX and EX by the crossing time of
the observed region:
t ![]() (R/cs
(R/cs![]() ), where cs is the speed-of-sound.
), where cs is the speed-of-sound.
If the X-ray-emitting gas is assumed to be volume-filling (f ![]() unity), the resulting values for
unity), the resulting values for ![]() and
and ![]() are then very similar
to the starburst's rates of kinetic energy deposition and
star formation respectively. As described above, Chandra images
(Fig. 1) show
that the X-ray-emitting gas does not have unit volume filling factor.
On morphological and physical grounds we have
argued that f is of-order 10-1.
This would mean that previous estimates
of
are then very similar
to the starburst's rates of kinetic energy deposition and
star formation respectively. As described above, Chandra images
(Fig. 1) show
that the X-ray-emitting gas does not have unit volume filling factor.
On morphological and physical grounds we have
argued that f is of-order 10-1.
This would mean that previous estimates
of ![]() and
and ![]() are overestimated by a factor of
are overestimated by a factor of ![]() 3.
3.
Optical Emission:
Optical data on the warm (T ![]() 104 K) ionized gas can be used
to determine the outflow rates
104 K) ionized gas can be used
to determine the outflow rates ![]() and
and ![]() in a way that
is quite analogous to the X-ray data.
In this case, the outflow velocities
can be directly measured kinematically from spectroscopy.
Martin (1999)
found the implied values for
in a way that
is quite analogous to the X-ray data.
In this case, the outflow velocities
can be directly measured kinematically from spectroscopy.
Martin (1999)
found the implied values for ![]() are comparable to (and may even exceed) the star-formation rate.
are comparable to (and may even exceed) the star-formation rate.
In favorable cases, the densities and thermal pressures can be directly
measured in the optical emission-line clouds using
the appropriate ratios of emission lines. The thermal pressure in these
clouds traces the ram-pressure in the faster outflowing wind that is
accelerating them (hydrodynamical simulations suggest that
Pram = ![]() Pcloud, where
Pcloud, where ![]() = 1 to 10). Thus, for a wind with a
mass-flux
= 1 to 10). Thus, for a wind with a
mass-flux ![]() that freely flows
at a velocity v into a solid angle
that freely flows
at a velocity v into a solid angle ![]() , we have
, we have
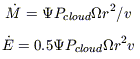
|
Based on observations and numerical models, the values
v ![]() 103 km s-1,
103 km s-1,
![]()
![]() a few, and
a few, and
![]() /4
/4![]()
![]() a few tenths are reasonable.
The radial pressure profiles
Pcloud(r) measured in superwinds by
Heckman, Armus, &
Miley (1990)
and Lehnert & Heckman
(1996)
then imply that
a few tenths are reasonable.
The radial pressure profiles
Pcloud(r) measured in superwinds by
Heckman, Armus, &
Miley (1990)
and Lehnert & Heckman
(1996)
then imply that ![]() is comparable to the star-formation rate
and that
is comparable to the star-formation rate
and that ![]() is comparable to the starburst
kinetic-energy injection rate (implying that radiative losses are
not severe).
is comparable to the starburst
kinetic-energy injection rate (implying that radiative losses are
not severe).
Interstellar Absorption-Lines: The use of interstellar absorption-lines to determine outflows rates offer several distinct advantages. First, since the gas is seen in absorption against the background starlight, there is no possible ambiguity as to the sign (inwards or outwards) of any radial flow that is detected, and the outflow speed can be measured directly (e.g. Fig. 2). Second, the strength of the absorption will be related to the column density of the gas. In contrast, the X-ray or optical surface-brightness of the emitting gas is proportional to the emission-measure. Thus, the absorption-lines more fully probe the whole range of gas densities in the outflow, rather than being strongly weighted in favor of the densest material (which may contain relatively little mass).
The biggest obstacle to estimating outflows rates is that the strong
absorption-lines are usually saturated, so that their equivalent width
is determined primarily by the velocity dispersion and covering factor,
rather
than by the ionic column density. In the cases where the rest-UV region
can be probed with adequate signal-to-noise
(Pettini et al. 2000;
Heckman & Leitherer
1997),
the total HI column in the outflow can be measured
by fitting the damping wings of the Ly![]() interstellar line,
while ionic columns may be estimated from the weaker (less saturated)
interstellar lines. In the
Heckman et al. (2000)
survey of the
NaD line, we estimated NaI columns in the outflows based
on the NaD doublet ratio
(Spitzer 1968),
and we then
estimated the HI column assuming that the gas obeyed the same
relation between NHI and NNaI as in
the Milky Way. These
HI columns agreed with columns estimated independently from the
line-of-sight
color excess E(B - V) toward the starburst,
assuming a Galactic gas-to-dust
ratio. From both the UV data and the NaD data, the typical inferred
values for NHI are of-order 1021
cm-2.
interstellar line,
while ionic columns may be estimated from the weaker (less saturated)
interstellar lines. In the
Heckman et al. (2000)
survey of the
NaD line, we estimated NaI columns in the outflows based
on the NaD doublet ratio
(Spitzer 1968),
and we then
estimated the HI column assuming that the gas obeyed the same
relation between NHI and NNaI as in
the Milky Way. These
HI columns agreed with columns estimated independently from the
line-of-sight
color excess E(B - V) toward the starburst,
assuming a Galactic gas-to-dust
ratio. From both the UV data and the NaD data, the typical inferred
values for NHI are of-order 1021
cm-2.
We can then adopt
a simple model of a superwind
flowing into a solid angle ![]() at a velocity v from a
minimum radius r* (taken to be the radius of the
starburst within which the flow originates). This implies:
at a velocity v from a
minimum radius r* (taken to be the radius of the
starburst within which the flow originates). This implies:
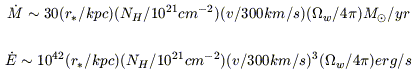
|
Based on this simple model,
Heckman et al. (2000)
estimated that the
implied outflow rates of cool atomic gas are comparable to the
star-formation rates (e.g. several tens of solar masses per year
in powerful starbursts). The flux of kinetic energy carried by
this material is substantial (of-order 10-1 of the kinetic
energy supplied by the starburst). We also estimated that ![]() 1%
of the mass in the outflow is the form of dust grains.
1%
of the mass in the outflow is the form of dust grains.
Summary: The various techniques for estimating the outflow rates in superwinds rely on simplifying assumptions (not all of which may be warranted). On the other hand, it is gratifying that the different techniques do seem to roughly agree: the outflows carry mass out of the starburst at a rate comparable to the star-formation rate and kinetic/thermal energy out at a rate comparable to the rate supplied by the starburst.