3. SUPERMASSIVE BLACK HOLES IN ACTIVE GALACTIC NUCLEI

The techniques that allow us to detect supermassive black holes in quiescent galaxies are rarely applicable to the hosts of bright AGNs. In the Seyfert 1 galaxies and in the handful of QSOs that are close enough that the black hole's sphere of influence has some chance of being resolved, the presence of the bright non-thermal nucleus (e.g. Malkan, Gorjian & Tam 1998) severely dilutes the very features which are necessary for dynamical studies. The only bright AGN in which a supermassive black hole has been detected by spatially-resolved kinematics is the nearby (Herrnstein et al. 1999; Newman et al. 2001) Seyfert 2 galaxy NGC 4258, which is blessed with the presence of an orderly water maser disk (Watson & Wallin 1994; Greenhill et al. 1995; Miyoshi et al. 1995). The radius of influence of the black hole at its center, ~ 0 ".15, can barely be resolved by HST but can be fully sampled by the VLBA at 22.2 GHz. Unfortunately, water masers are rare and of the handful that are known, only in NGC 4258 are the maser clouds distributed in a simple geometrical configuration that exhibits clear Keplerian motion around the central source (Braatz et al. 1996; Greenhill et al. 1996, 1997; Greenhill, Moran & Herrnstein 1997; Trotter et al. 1998). Black hole demographics in AGNs must therefore proceed via alternate routes.

Dynamical modeling of the broad emission line region (BLR) constitutes a viable alternative to spatially-resolved kinematical studies. According to the standard model, the BLR consists of many (10^{7 - 8}, Arav et al. 1997, 1998; Dietrich et al. 1999), small, dense (N_e ~ 10^{9 - 11} cm^-3), cold (T_e ~ 2 × 10⁴ K) photoionized clouds (Ferland et al. 1992), localized within a volume of a few light days to several tens of light weeks in diameter around the central ionization source (but see also Smith & Raine 1985, 1988; Pelletier & Pudritz 1992; Murray et al. 1995; Murray & Chiang 1997; Collin-Souffrin et al. 1988). As such, the BLR is, and will likely remain, spatially unresolved. In the presence of a variable non-thermal nuclear continuum, however, the responsivity-weighted radius R_BLR of the BLR is measured by the light-travel time delay between emission and continuum variations (Blandford & McKee 1982; Peterson 1993; Netzer & Peterson 1997; Koratkar & Gaskell 1991). If the BLR is gravitationally bound, the central mass is given by the virial theorem as M_virial = v_BLR²R_BLR / G, where the FWHM of the emission lines (generally H) is taken as being representative of the rms velocity v_BLR, once assumptions are made about the BLR geometry. In a few cases, independent measurements of R_BLR and v_BLR have been derived from different emission lines: it is found that the two quantities define a "virial relation" in the sense v_BLR ~ r^-1/2 (Koratkar & Gaskell 1991; Wandel, Peterson & Malkan 1999; Peterson & Wandel 2000), suggesting a simple picture of a stratified BLR in Keplerian motion.

On the downside, mapping the BLR response to continuum variations requires many (~ 10^{1 - 2}) repeated observations taken at closely spaced time intervals, t 0.1R_BLR/c. Moreover, the observations can be translated into black hole masses only if a series of reasonable, but untested, assumptions are made regarding the geometry, stability and velocity structure of the BLR, the radial emissivity function of the gas, and the geometry and location (relative to the BLR) of the ionizing continuum source. If a wrong assumption is made, systematic errors of a factor ~ 3 can result (Krolik 2001). The uncertainties surrounding reverberation mapping has made the derived black hole masses an easy target for critics (e.g. Richstone et al. 1998; Ho et al. 1999). On the other hand, because the BLR gas samples a spatial region very near to the black hole, there is almost no possibility of making the much larger errors in M that have plagued the ground-based stellar kinematical studies (Magorrian et al. 1998). Thanks to the efforts of international collaborations, reverberation mapping masses are now available for 17 Seyfert 1 galaxies and 19 QSOs (Wandel, Peterson & Malkan 1999; Kaspi et al. 2000).

Taken at face value, reverberation mapping radii are found to correlate with the non-thermal optical luminosity of the nuclear source. While the exact functional form of the dependence is debated (Koratkar & Gaskell 1991; Kaspi et al. 1996, 2000; Wandel, Peterson & Malkan 1999), the R_BLR - L relation can potentially provide an inexpensive way of bypassing reverberation mapping measurements on the way to determining black hole masses.

3.1. AGN Black Hole Demographics from the M - M_bulge Relation

With one exception (Ferrarese et al. 2001), black hole demographic studies for AGNs have been based on the M - M_B, rather than on the M - , relation for the simple reason that few accurate measurements exist in AGN hosts (e.g. Nelson & Whittle 1995). L_bulge, on the other hand, is more easily measured than (though not necessarily more accurately measured, as discussed below). The modest sample of AGNs with reverberation mapping black hole masses is often augmented using masses derived from the R_BLR - L relation (Wandel 1999; Laor 1998, 2001; McLure & Dunlop 2000). For a sample of 14 PG quasars, Laor (1998) reported reasonable agreement with the M - M_B relation derived by Magorrian et al. (1998) for quiescent galaxies, finding <M / M_bulge> = 0.006. Seyfert 1 galaxies define a significantly different correlation according to Wandel (1999): <M / M_bulge> = 0.0003. Most recently, McLure & Dunlop (2000) have reanalyzed the QSO sample of Laor and the Seyfert sample of Wandel (the first augmented with almost as many new objects and both with new spectroscopic and/or photometric data for the existing objects). McLure & Dunlop split the difference of the two ealier studies by obtaining <M / M_bulge> = 0.0025. They find no statistical difference between Seyfert 1s and QSOs.

The different conclusions reached by these authors can be traced to a number of factors.

• Bulge magnitudes are at the heart of the problem for the Seyfert sample (McLure & Dunlop 2000; Laor 2001). Wandel used luminosities derived (by Whittle et al. 1992) using the Simien & de Vaucouleurs (1986) empirical correlation between galaxy type and bulge/disk ratio. HST images allowed McLure & Dunlop to perform a proper disk/bulge decomposition, which produces bulges 1 - 3.5 magnitudes fainter than assumed by Wandel (1999), hence larger M / M_bulge.

• Overestimated black hole masses seem to be responsible for the large <M / M_bulge> measured by Laor. Here, the bolometric non-thermal nuclear luminosity used in estimating R_BLR from the R_BLR - L relation is a factor ~ 3 larger in Laor than in McLure & Dunlop (for the same cosmology). Everything else being equal, this leads to a factor ~ 2 increase in the black hole masses. It is unclear which luminosities are more correct; however it seems that the McLure & Dunlop values are to be preferrred for the following reason. The R_BLR - L relation is defined using monochromatic luminosity (at 5100 Å in Kaspi et al. 2000, and 4800 Å in Kaspi et al. 1996). This can be transformed to a bolometric luminosity by assuming a power law of given spectral index for the nuclear spectrum. McLure & Dunlop used monochromatic luminosities applied to the Kaspi et al. (2000) relation, while Laor started from bolometric luminosities (from Neugebauer et al. 1987), applied a constant bolometric correction, and then used the Kaspi et al. (1996) relation. The more direct route used by McLure & Dunlop (which bypasses the need for a bolometric correction) seems to be preferable.

We have recomputed the data from the Wandel (1999) and McLure & Dunlop (2000) studies under a uniform set of assumptions, as follows:

• H₀ = 75 km s^-1 Mpc^-1. While black hole masses are independent of cosmology, bulge magnitudes are not. For nearby quiescent galaxies with dynamically detected black holes, distances are estimated directly, mainly using the surface brightness fluctuation method (SBF). SBF distances to galaxies in the (mostly) unperturbed Hubble flow lead to H₀ = 70 - 77 km s^-1 Mpc^-1 (Ferrarese et al. 2000; Tonry et al. 2001); H₀ = 75 km s^-1 Mpc^-1 therefore gives distances, for the distant QSOs and Seyfert 1s, on the same distance scale used for the nearby quiescent galaxies. Using H₀ = 50 km s^-1 Mpc^-1 instead, as in McLure and Dunlop, would inflate AGN bulge luminosities by a factor 2.25 (and the masses by a factor ~ 2.7; see below).

• R_BLR = 32.9( L₅₁₀₀ / 10⁴⁴ergs s^-1)^0.7 light days (Kaspi et al. 2000). While it is likely that the slope of this correlation will be refined once accurate estimates of R_BLR are obtained at low and high luminosities, this is currently the best estimate of the functional form of the R_BLR - L relation. Because all QSOs have higher luminosities than the objects that define the R_BLR - L relation, adopting R_BLR ( L₅₁₀₀)^0.5 (e.g. Kaspi et al. 1996) would lead to estimates of R_BLR and M that are 1.5 to 3 times smaller respectively.

• v_BLR = 3 / 2FWHM(H), i.e. the BLR is spherical and characterized by an isotropic velocity distribution. This differs from the assumption made by McLure & Dunlop that the BLR is a thin, rotation-dominated disk, i.e. v = 1.5FWHM(H), which predicts velocities 1.7 times larger and black holes masses three times greater.

• M/L L^0.18 (Magorrian et al. 1998). This is the relation defined by the local sample of quiescent galaxies, for which Merritt & Ferrarese (2001a) derived M / M_bulge = 0.13%. Fundamental plane studies (Jorgensen, Franx & Kjaergaard 1996) point to a steeper dependence: M/L L^0.34. Accounting for the proper normalization, and given the range in luminosity spanned by the QSOs and Seyfert 1 galaxies, using the latter relation would increase all inferred M / M_bulge ratios by a factor ~ 2.5.

Figure 8. The M / Mbulge relation for quiescent galaxies (solid black dots, with best fit given by the green line), Seyfert 1 galaxies (blue triangles) and nearby QSOs (red circles). The data are taken from Ferrarese & Merritt (2000), McLure & Dunlop (2000) and Wandel, Peterson & Malkan (1999). When necessary, bulge magnitudes are converted to Johnsons B by adopting V - R = 0.59 and B - V = 0.93. The size of the symbols for the AGNs is proportional to the H FWHM: the nominal distinction between narrow and broad line AGNs occurs at the FWHM represented by the symbol size used in the legend. The yellow line represents the best fit to the nearby quiescent galaxies derived by Magorrian et al. (1998); the green line is fit to the black hole masses from Merritt & Ferrarese (2001a) (shown as filled circles). The dotted black lines are the loci for which the black hole mass is a fixed percentage of the bulge mass. The arrows in the upper left corner represent the change in M or Mbulge produced under assumptions different from the ones detailed in the text.

The results are shown in Figure 8. We draw the following conclusions.

1. The Seyfert, QSO and quiescent galaxy samples are largely consistent. A simple least-squares fit gives <M / M_bulge> = 0.09% (QSOs) and 0.12% (Seyferts), compared with <M / M_bulge> = 0.13% for quiescent galaxies (Merritt & Ferrarese 2001a). We further note that the disk/bulge decompositions for two of the objects with low M / M_bulge, 0.001% - 0.001%, are deemed of lower quality (McLure & Dunlop 2000). Thus it does not appear to be the case, as suggested by Richstone et al. (1998) and Ho (1999), that supermassive black holes in AGN are undermassive relative to their counterparts in quiescent galaxies. In fact, assuming a flattened BLR geometry would further increase the AGN masses.

2. <M / M_bulge> in AGNs is lower, by a factor ~ 6, than predicted by the Magorrian (1998) relation. This is further evidence that the mass estimates derived from ground-based kinematics were systematically in error.

3. In view of recent claims, it is interesting to ask whether narrow line Seyfert 1s and QSOs (Osterbrock & Pogge 1985) contain smaller black holes compared with the rest of the AGN sample (Véron-Cetty, Véron & Goncalves 2001 and references therein; Mathur et al. 2001). The size of the symbols in Figure 8 is proportional to the FWHM of the H line: the boundary between regular and narrow line objects corresponds to the size used in the figure legend. No correlation between line width and M / M_bulge is readily apparent for the Seyferts, while a hint might be present for the QSOs. On the other hand, bulge/disk decompositions are less accurate for most of the narrow line QSOs, and it is possible that bulge luminosities in these objects have been overestimated.

4. The large uncertanities in the data, and the large intrinsic scatter in the M - M_B relation, make it very difficult to test whether the relation between M and M_bulge is linear. However, an ordinary least square fit to the data produces slopes consistent, at the 1 level, with a linear relation for both the QSO and Seyfert 1 samples (cf Laor 2001).

3.2. AGN Black Hole Demographics from the M - Relation

Because of its large intrinsic scatter, there is little more that can be learned about black hole demographics from the M - M_B relation. An alternative route is suggested by the M - relation for quiescent galaxies, which exhibits much less scatter. Very few accurate measurements of are available in AGNs, due to the difficulty of separating the bright nucleus from the faint underlying stellar population. The first program to map AGNs onto the M - relation was undertaken by Ferrarese et al. (2001). Velocity dispersions in the bulges of six galaxies with reverberation mapping masses were obtained, thus producing the first sample of AGNs for which both the black hole mass and the stellar velocity dispersion are accurately known (with formal uncertainties of 30% and 15% respectively).

Figure 9 shows the relation between black hole mass and bulge velocity dispersion for the six reverberation-mapped AGNs observed by Ferrarese et al. (2001), plus an additional object with a high-quality from the literature (Nelson & Whittle 1995). The quiescent galaxies (Sample A from Ferrarese & Merritt 2000) are shown by the black dots. The consistency between black hole masses in active and quiescent galaxies is even more striking here than in the M - M_bulge plot. The only noticeable difference between the two samples is a slightly greater scatter in the reverberation mapping masses (in spite of similar, formal error bars). Narrow line Seyfert 1 galaxies do not stand out in any way from the rest of the AGN sample.

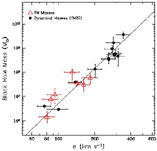
Figure 9. Black hole mass versus central velocity dispersion for seven reverberation-mapped AGNs with accurately measured velocity dispersions, compared with the nearby quiescent galaxy sample of Ferrarese & Merritt (2000) (plot adapted from Ferrarese et al. 2001).