4. RECENT AND FUTURE REFINEMENTS OF THE M - RELATION

4.1. M33 - No Supermassive Black Hole?

The smallest nuclear black holes whose masses have been securely established are in the Milky Way and M32, both of which have M 3 × 10⁶ M (Table 1). How small can supermassive black holes be? Some formation scenarios (e.g. Haenhelt, Natarajan & Rees 1998) naturally predict a lower limit of ~ 10⁶ M. Black holes of lower mass have been hypothesized to hide within off-nuclear "Ultra Luminous X-Ray Sources" (ULXs: Matsumoto et al. 2001; Fabbiano et al. 2001), but their formation mechanisms are envisioned to be completely different (e.g. Miller & Hamilton 2001). Observationally, a black hole with M 10⁶ M could only be resolved in a very nearby galaxy. An obvious candidate is the Local Group late type spiral M33: the absence of an obvious bulge, and the low central stellar velocity dispersion ( ~ 20 km s^-1, Kormendy & McLure 1993) both argue for a very small black hole. According to the M - relation (Eq. 2), M ~ 3 × 10³ M, but a range of at least 1 - 10 × 10³ M is allowed given the uncertainties in the slope of the relation.

We show in Figure 10 the rotation curve and velocity dispersion profile of the M33 nucleus obtained from HST/STIS data. There is an unambiguous decrease in the stellar velocity dispersion toward the center of the nucleus: the central value is 24±3 km s^-1, significantly lower than its value of ~ 35±5 km s^-1 at ±0.3" 1.2 pc. The rotation curve is consistent with solid-body rotation. A dynamical analysis (Merritt, Ferrarese & Joseph 2001) gives an upper limit to the central mass of ~ 3 × 10³ M. While this is tantalizingly similar to the masses inferred for ULXs (Matsumoto et al. 2001; Fabbiano, Zezas & Murray 2001), the consistency of this upper limit with the M - relation (Figure 10 and Eq. 2) does not allow us to conclude that the presence of a black hole in M33 would demand a formation mechanism different from the one responsible for the creation of supermassive black holes in other galaxies.

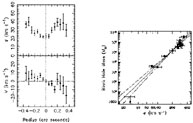
Figure 10. Upper limit on the mass of the black hole in M33 (adapted from Merritt, Ferrarese & Joseph 2001). Left: stellar rotation curve and velocity dispersion profile. Right: the M - relation including the upper limit on M.

Can we expect to hear about the detection of 10⁶ M nuclear black holes in galaxies other than M33 within the next few years? The remainder of this section summarizes ongoing efforts and discusses what we are likely to learn.

4.2. Other New Data from HST

In the next few years, attempts will be made to detect and dynamically measure the masses of black holes at the centers of dozens of galaxies. The Space Telescope alone is committed to devoting several hundred orbits to the cause: roughly 130 galaxies have been or will be observed with STIS within the next two years as part of ~ 10 separate projects.

News from some of these projects is already starting to circulate. Sarzi et al. (2001) report results from an HST gas dynamical study of the nuclei of 24 nearby, weakly active galaxies. Four of the galaxies were found to have kinematics consistent with the presence of dust/gas disks (the prototype of which was detected in NGC 4261 by Jaffe et al. 1994); the authors conclude that in only one of the four galaxies (NGC 2787) can the kinematics provide meaningful constraints on the presence of a supermassive black hole. Barth et al. (2001) report the successful detection of a nuclear black hole in NGC 3245, one of six broad-lined AGNs targeted by the team with HST. The STIS Instrument Development Team (IDT) has obtained stellar absorption line spectra for ~ 12 galaxies and the data for the first of these, M32, have been published (Joseph et al. 2001). The largest sample of stellar dynamical data (roughly 40 galaxies, about half of which have already been observed) will belong to the "Nuker" team. Data and a dynamical analysis have been published for one of these galaxies (NGC 3379, Gebhardt et al. 2001a) and preliminary masses for an additional 14 galaxies have been tabulated by Gebhardt et al. (2000b) and again by Kormendy & Gebhardt (2001). Mass estimates were apparently revised in the second tabulation, some by as much as 50%. We adopt the most recent values in the discussion that follows, pending publication of the full data and analyses.

We can update the M - relation using the additional black hole masses that have been published over the last year. In addition to the 12 galaxies used by Ferrarese & Merritt (2000) to define the M - relation, 10 galaxies listed in Table 1 also have FWHM/2r_h < 1. A regression fit accounting for errors in both coordinates (Akritas & Bershady 1996) to the expanded sample of 22 galaxies gives

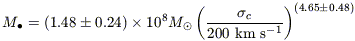
(2)

in good agreement with previous determinations (Ferrarese & Merritt 2000; Merritt & Ferrarese 2001b). Within this sample, the two subsamples containing only stellar kinematical or stellar dynamical data produce fits with slopes of ~ 4.5, in agreement with each other and with the slope quoted for the complete sample.

However, something interesting happens when the eight galaxies in Table 1 for which r_h has not been resolved are added to the sample (all of the mass determinations in these galaxies are based on stellar dynamics). Figure 11 shows the slope of the M - relation obtained from the stellar dynamical mass estimates when various cutoffs are placed on the quality of the data. If the complete sample is used (including all entries in Table 1 down to NGC 2778), the slope becomes quite shallow, 3.81±0.33. When only the best-resolved galaxies are included, FWHM / r_h < 0.2, the slope increases to 4.48±0.12, identical to the value obtained from the gas dynamical masses alone. Mass estimates based on the dynamics of gas disks are expected to be more accurate than estimates from stellar dynamics at equal resolution since the inclination angle of the disk can be measured and (if the motions are in equilibrium) the circular orbital geometry is simpler (Faber 1999). From Figure 11, we conclude that the inclusion of masses derived from data that do not properly sample the black hole's sphere of influence biases the slope of the relation. A similar conclusion was reached by Merritt & Ferrarese (2001b).

We also show in Figure 11 the results of least-squares fits using a simpler algorithm that does not account for measurement errors. This is the same algorithm used by Gebhardt et al. (2000a). As pointed out by Merritt & Ferrarese (2001b), not accounting for measurement errors biases the slope too low: the inferred slope for the complete sample of stellar dynamical masses falls to ~ 3.5 using the simpler algorithm, similar to the slope quoted by Gebhardt et al. (2000a) and Kormendy & Gebhardt (2001). Thus the lower slope quoted by those authors is due to the inclusion of less accurate data points and to the use of a less precise regression algorithm.

Figure 11. The slope of the M - relation as derived from stellar dynamical data as a function of data quality. Solid circles are slopes derived from a regression algorithm that accounts for errors in both variables; open circles are from a standard least-squares routine. Solid line is the slope derived from gas dynamical data, for which the black hole's sphere of influence was always resolved.

4.3. The Future

We noted above that a total of ~ 130 galaxies have been or will be observed with HST during the next two years with the hope of constraining the mass of the central black hole. How many of these new data sets will in fact lead to stringent constraints on M? In Figure 2 we plot the expected radius of influence of the black hole versus FWHM/2r_h for all galaxies for which a reliable distance (or redshift) and velocity dispersion could be gathered from the literature. Black hole masses have been estimated from the M - relation, Eq. (2). We argued above that the condition FWHM/2r_h 1.0, compounded by the low S/N characteristic of HST data, will likely lead to weak constraints or biased determinations of M, particularly in the case of stellar absorption line data.

Figure 2 shows that the black hole's sphere of influence will be resolved in less than half of these galaxies. Less than one quarter will be resolved as well or better than NGC 3379 (FWHM/2r_h 0.4), for which the constraints on M are weak (Section 2.2). Among the galaxies slated to be observed in ionized gas, the preliminary results of Sarzi et al. (2001) suggest that few will be found to have the well-ordered disks that are necessary for secure estimates of M.

Many of the "Sample A" galaxies from Ferrarese & Merritt (2000) were originally targeted for observation because of their exceptionally favorable properties, such as nearness (the Milky Way, M32), existence of a well-ordered maser disk (NGC 4258), etc. It is unlikely that many more galaxies will turn out to have equally favorable properties.

The majority of the targeted galaxies are expected to have black holes with masses of order 10⁸ M. This range is already well sampled by the current data; however the new detections might provide useful information about the scatter of the M - relation. Only a handful of black holes with masses 10⁹ M or ~ 10⁷ M will be detected, and probably none in the < 10⁷ M range. Probing the low and high mass end of the M - relation is of particular interest since the slope and scatter of the relation have important implications for hierarchical models of galaxy formation (Haehnelt, Natarajan, & Rees 1998; Silk & Rees 1998; Haehnelt & Kauffmann 2000) and the effect of mergers on subsequent evolution (Cattaneo et al. 1999). The fact that the new observations will not appreciably extend the range of masses is not due to poor planning: the simple fact is that very small or very massive black holes are found in galaxies which are not close enough to resolve their sphere of influence using current optical/near infrared instrumentation.

It is our opinion that the future of the M - relation relies on methods other than traditional dynamical studies. An aggressive campaign to reverberation map a large sample of AGNs appears to be the obvious solution. The recent results from Ferrarese et al. (2001) show that reverberation mapping can produce mass estimates with a precision comparable to traditional dynamical studies. Although the obvious drawback is that it is only applicable to the ~ 1% of galaxies with Type 1 AGN, reverberation mapping is intrinsically unbiased with respect to black hole mass, provided the galaxies can be monitored with the appropriate time resolution: while dynamical methods rely on the ability to spatially resolve the black hole's sphere of influence, reverberation mapping samples a region which is per se unresolvable. Furthermore, reverberation mapping can probe galaxies at high redshifts and with a wide range of nuclear activity, opening an avenue to explore possible dependences of the M - relation on redshift and activity level.