Invited review, Ringberg Workshop: "Galaxies in the
Young Universe II", Aug. 2-6 1999, Hans Hippelein (ed.),
Springer-Verlag;
astro-ph/9911204
EARLY CHEMICAL EVOLUTION OF GALAXIES
B.E.J. Pagel
Astronomy Centre, CPES,
University of Sussex,
Brighton BN1 9QJ, UK
Abstract. Initial conditions are set by Big bang nucleosynthesis
from which we know
that 90 per cent of baryons are dark and have essentially unknown chemical
composition. In our own Galaxy, there are many clues from individual
stars in different populations whereas in elliptical galaxies the data
largely come
from integrated spectra, but these raise problems enough like the Mg/Fe
and G-dwarf problems. Irregular and blue compact galaxies display
the primary-secondary transition in
N/O; this in turn may be relevant to element ratios observed in damped
Lyman- systems at high
red-shift, which offer rather little evidence
for pure SNII synthesis such as is found in the Galactic halo stars. A
recent estimate of past star formation rates as a function of red-shift
is presented
and the appropriateness of the conventional conversion factor of 42 from
SFR to metal production is discussed. For any reasonable value of this
conversion factor, it is clear that most of the metals existing at
z = 2.5 have yet to be detected.
systems at high
red-shift, which offer rather little evidence
for pure SNII synthesis such as is found in the Galactic halo stars. A
recent estimate of past star formation rates as a function of red-shift
is presented
and the appropriateness of the conventional conversion factor of 42 from
SFR to metal production is discussed. For any reasonable value of this
conversion factor, it is clear that most of the metals existing at
z = 2.5 have yet to be detected.
 INTRODUCTION
INTRODUCTION
 CHEMICAL EVOLUTION OF THE MILKY WAY
CHEMICAL EVOLUTION OF THE MILKY WAY
 ELLIPTICAL GALAXIES
ELLIPTICAL GALAXIES
 ABUNDANCES AT HIGH RED-SHIFT
ABUNDANCES AT HIGH RED-SHIFT
 REFERENCES
REFERENCES
1. INTRODUCTION
Initial conditions set by Big Bang nucleosynthesis are
Y = .24, Z = 0 for helium (e.g.
Pagel 2000)
and heavy elements respectively, D/H = 4 × 10-5
(Levshakov, Tytler &
Burles 1998)
and 7Li/H = 1.7 × 10-10
(Bonifacio & Molaro
1997).
The D/H ratio is the best indication of the overall
density of baryons in the universe, which can be expressed as
0.03 
 B
h702
B
h702
 0.04, similar to the density of
Lyman-
0.04, similar to the density of
Lyman- forest gas at
red-shifts 2 to 3
(Rauch et al. 1998),
whereas the mass in visible stars in galaxies is given by
forest gas at
red-shifts 2 to 3
(Rauch et al. 1998),
whereas the mass in visible stars in galaxies is given by
 *
h70
*
h70  0.0035
(Fukugita, Hogan &
Peebles 1998),
i.e. only 1/10 as much. Thus 90 per cent of baryonic matter is
unseen and of unknown chemical composition, although it is reasonable to
speculate that most of it is still intergalactic gas with Z now
somewhere between
0.3 Z
0.0035
(Fukugita, Hogan &
Peebles 1998),
i.e. only 1/10 as much. Thus 90 per cent of baryonic matter is
unseen and of unknown chemical composition, although it is reasonable to
speculate that most of it is still intergalactic gas with Z now
somewhere between
0.3 Z (Mushotzky & Loewenstein
1997) and
0.1 Z
(Mushotzky & Loewenstein
1997) and
0.1 Z or less
(Cen & Ostriker 1999).
or less
(Cen & Ostriker 1999).
The remainder of cosmic chemical evolution is the result of star
formation, the
history of which has been extensively studied by Madau and others
(Madau et al. 1996;
Steidel et al. 1999;
Pettini 1999)
using data from red-shift surveys, Lyman break galaxies etc.
(see Figure 1). Thus we now have a fair idea
about global star formation rates
since z = 4.5, but ironically we do not know how to associate
them with particular
types of galaxies. The good news is that the integral over this version
of the SFR history does come close to the estimated cosmic density of
stars as given above,
and it seems that about 1/4 of the stars were formed at red-shifts
greater than 2.5, over 1010 years ago. This raises the
question of what happened to all the metals they made, to which I return
in the last section.
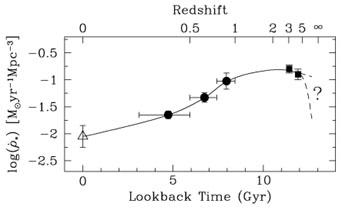
|
Figure 1. Global comoving star formation
rate density vs. lookback time
compiled from wide-angle ground-based surveys
(Steidel et al. 1999
and references therein) assuming E-de S cosmology with h = 0.5,
after
Pettini (1999).
Courtesy Max Pettini.
|
2. CHEMICAL EVOLUTION OF THE MILKY WAY
The Galactic halo, bulge and disk(s) are all relevant to early times,
only the thin
disk being younger than the bulge and thick disk. The respective roles of
hierarchical clustering, mergers and monolithic collapse are still not
very clear;
probably all play a role, but the halo and bulge share a low specific
angular momentum while the thick and thin disks share a high one and
may result from
later accretion of gas by the bulge, which would then resemble an E-galaxy.
However, it is also possible that the bulge evolved from the disk by way
of a bar.
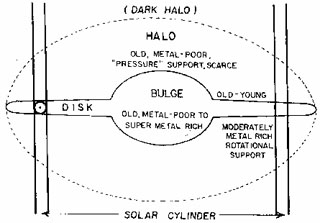
|
Figure 2. Schematic cross-section through
the Galaxy.
|
In any case, the stellar dynamics of the halo favour what
Thomas, Greggio & Bender
(1999)
refer to as a "fast clumpy collapse", basically the old idea of
Eggen, Lynden-Bell &
Sandage (1962)
placed in the context of modern hierarchical clustering
scenarios. One point of interest is the metallicity distribution
function (MDF), recently extended to very low metallicities by
Beers et al. (1998).
The MDF is essentially the modified Simple-model type distribution
originally noted by
Hartwick (1976),
with a peak at about 1/10 of the true yield, down to [Fe/H]
 - 3. Below that it begins
to fall off and there are virtually no stars
(compared to a predicted number of about 10) below -4, which could
represent enrichment either from a hypothetical Population III or from
contamination of low-mass stars by a nearby supernova.
- 3. Below that it begins
to fall off and there are virtually no stars
(compared to a predicted number of about 10) below -4, which could
represent enrichment either from a hypothetical Population III or from
contamination of low-mass stars by a nearby supernova.
A significant clue to early Galactic chemical evolution comes from the
relation between oxygen and
 -particle elements, thought
to come exclusively or mainly
from type II supernovae, and iron, more than half of which in the Solar
System comes
from Type Ia. Fig 3 suggests that there is a
plateau in O,
-particle elements, thought
to come exclusively or mainly
from type II supernovae, and iron, more than half of which in the Solar
System comes
from Type Ia. Fig 3 suggests that there is a
plateau in O, / Fe at low
metallicities (assumed to represent early times), but there is currently a
controversy in the case of oxygen. Abundances derived from the forbidden
[OI] line, which is probably the most reliable source when it is not too
weak, suggest a plateau, but from measurements of the near UV OH bands
in dwarfs and subgiants, both
Israelian, García Lopez
& Rebolo (1998)
and Boesgaard et al. (1999)
have derived a rising trend with diminishing [Fe/H] more or less
following the
open squares in the top panel of Figure 3. In
contrast,
Fulbright & Kraft
(1999)
have studied the [OI] spectral region in two of the extreme cases and
find lower O/Fe ratios fitting the plateau. There are technical
difficulties in both methods:
the OH bands are subject to uncertainties in UV continuum absorption (cf.
Balachandran & Bell 1998
on solar beryllium abundance) and effective temperature,
while the forbidden line in the relevant cases is so very weak that the
definition of the continuum becomes a crucial source of uncertainty.
/ Fe at low
metallicities (assumed to represent early times), but there is currently a
controversy in the case of oxygen. Abundances derived from the forbidden
[OI] line, which is probably the most reliable source when it is not too
weak, suggest a plateau, but from measurements of the near UV OH bands
in dwarfs and subgiants, both
Israelian, García Lopez
& Rebolo (1998)
and Boesgaard et al. (1999)
have derived a rising trend with diminishing [Fe/H] more or less
following the
open squares in the top panel of Figure 3. In
contrast,
Fulbright & Kraft
(1999)
have studied the [OI] spectral region in two of the extreme cases and
find lower O/Fe ratios fitting the plateau. There are technical
difficulties in both methods:
the OH bands are subject to uncertainties in UV continuum absorption (cf.
Balachandran & Bell 1998
on solar beryllium abundance) and effective temperature,
while the forbidden line in the relevant cases is so very weak that the
definition of the continuum becomes a crucial source of uncertainty.
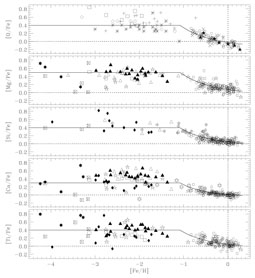
|
Figure 3. Abundance ratios of oxygen and
 -elements to iron, plotted
against [Fe/H] for stellar samples from the Galactic disk and halo,
after
Pagel & Tautvaisiene
(1995).
The solid line and curve represent a simple analytical
Galactic chemical evolution model. -elements to iron, plotted
against [Fe/H] for stellar samples from the Galactic disk and halo,
after
Pagel & Tautvaisiene
(1995).
The solid line and curve represent a simple analytical
Galactic chemical evolution model.
|
However this controversy comes out, the
O, enhancement is not
universal, as has been shown, e.g. by
Nissen & Schuster
(1997);
there are "anomalous" halo
stars which have more solar-like element ratios even at quite low
metallicities, a feature that is also found in the Magellanic Clouds and
can be explained on the
basis of slower star formation rates and effective yields diminished by
outflows (e.g.
Pagel & Tautvaisiene
1998).
However, within the halo the presence
of "anomalies" shows no obvious relation with extreme kinematic
properties that might be signatures of a captured satellite
(Stephens 1999).
enhancement is not
universal, as has been shown, e.g. by
Nissen & Schuster
(1997);
there are "anomalous" halo
stars which have more solar-like element ratios even at quite low
metallicities, a feature that is also found in the Magellanic Clouds and
can be explained on the
basis of slower star formation rates and effective yields diminished by
outflows (e.g.
Pagel & Tautvaisiene
1998).
However, within the halo the presence
of "anomalies" shows no obvious relation with extreme kinematic
properties that might be signatures of a captured satellite
(Stephens 1999).
Within the thick disk, the
 / Fe ratio is remarkably
uniform, even up to
quite high metallicities, indicating an old "get rich quick"
population. This is well brought out by the work of
Fuhrmann (1998)
on Mg, shown in Figure 4, and
in a still unpublished study of oxygen by
Gratton et al. (1996),
and it may be that this trend is continued in the bulge (cf.
Rich 1999).
The data cast an interesting light on the formation of the thick disk,
since they indicate a hiatus in star
formation during which Fe/
/ Fe ratio is remarkably
uniform, even up to
quite high metallicities, indicating an old "get rich quick"
population. This is well brought out by the work of
Fuhrmann (1998)
on Mg, shown in Figure 4, and
in a still unpublished study of oxygen by
Gratton et al. (1996),
and it may be that this trend is continued in the bulge (cf.
Rich 1999).
The data cast an interesting light on the formation of the thick disk,
since they indicate a hiatus in star
formation during which Fe/ increased but overall metallicity diminished,
maybe from inflow of relatively unprocessed material, e.g. in a merger,
before the stars now belonging to the thin disk were formed.
increased but overall metallicity diminished,
maybe from inflow of relatively unprocessed material, e.g. in a merger,
before the stars now belonging to the thin disk were formed.
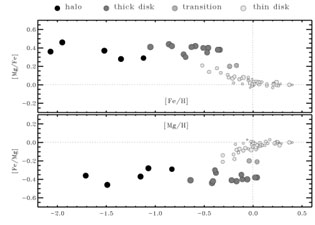
|
Figure 4. [Mg/Fe] vs [Fe/H] and [Fe/Mg] vs
[Mg/H] for stars of the Galactic halo, thick disk and thin disk, after
Fuhrmann (1998).
Courtesy Klaus Fuhrmann.
|
Returning to the earliest stage of evolution of the Population II halo,
when we consider a regime in which [Fe/H] < - 2.5 or so, we reach a
stage where pollution by a single supernova becomes significant over a
region the size of a globular cluster or superbubble of the order of
105
M . Metallicity
(however defined) then becomes a poor clock and strange patterns appear,
accompanied by significant scatter
(McWilliam 1997).
There are marked changes within the iron group, with Cr, Mn (and Cu)
going down relative to iron and Co going up.
Ryan, Norris & Beers
(1996)
suggest that at these low levels [Fe/H]
is an increasing function of the mass of an individual supernova, and
Tsujimoto & Shigeyama
(1998)
have estimated revised stellar yields as a function of progenitor
mass on this basis. Most yields increase, with the conspicuous exception
of the r-process, whose representative Eu/Fe has a large scatter and may be
anti-correlated
with [Fe/H]. Ba and Sr also mainly come from the r-process at these low
metallicities and have even more scatter because the s-process can also
contribute in evolved
stars or stars with evolved companions. In a model recently put forward by
Tsujimoto, Shigeyama &
Yoshii (1999),
stars form in superbubbles dominated by a
single supernova, so that their composition is a weighted mean of the
interstellar medium (with [Eu/Fe]
. Metallicity
(however defined) then becomes a poor clock and strange patterns appear,
accompanied by significant scatter
(McWilliam 1997).
There are marked changes within the iron group, with Cr, Mn (and Cu)
going down relative to iron and Co going up.
Ryan, Norris & Beers
(1996)
suggest that at these low levels [Fe/H]
is an increasing function of the mass of an individual supernova, and
Tsujimoto & Shigeyama
(1998)
have estimated revised stellar yields as a function of progenitor
mass on this basis. Most yields increase, with the conspicuous exception
of the r-process, whose representative Eu/Fe has a large scatter and may be
anti-correlated
with [Fe/H]. Ba and Sr also mainly come from the r-process at these low
metallicities and have even more scatter because the s-process can also
contribute in evolved
stars or stars with evolved companions. In a model recently put forward by
Tsujimoto, Shigeyama &
Yoshii (1999),
stars form in superbubbles dominated by a
single supernova, so that their composition is a weighted mean of the
interstellar medium (with [Eu/Fe]
 [
[ /Fe] = constant) and
supernova ejecta. Fe/H
increases with the mass of the supernova while Eu/Fe decreases, leading
to an
anti-correlation with scatter superimposed until the ISM is sufficiently
enriched to take over and normal Galactic chemical evolution proceeds.
/Fe] = constant) and
supernova ejecta. Fe/H
increases with the mass of the supernova while Eu/Fe decreases, leading
to an
anti-correlation with scatter superimposed until the ISM is sufficiently
enriched to take over and normal Galactic chemical evolution proceeds.
Further evidence for inhomogeneity comes from the abundances of the
light elements
6Li, beryllium and boron, which show an unexpected "primary"
behaviour - at least relative to iron - down to
very low metallicities. This cannot be understood on the basis of
spallation of interstellar CNO nuclei by primary cosmic ray protons and
 -particles; these
give a reasonable explanation for their abundances in the Sun and
Population I stars
in general but led to an expectation of secondary behaviour (Be,B/O
-particles; these
give a reasonable explanation for their abundances in the Sun and
Population I stars
in general but led to an expectation of secondary behaviour (Be,B/O
 O/H)
with diminishing metallicity.
(1)
There are also
energetic problems with the production by interstellar spallation at low
metallicity
(Ramaty et al. 1997).
Thus various inhomogeneous processes have been proposed,
beginning with the hypothesis of
Duncan, Lambert & Lemke
(1992)
that fast CNO nuclei in primary cosmic rays are reponsible, and that their
abundance is dominated
by supernova ejecta rather than the interstellar medium. A more detailed
model by
Ramaty & Lingenfelter
(1999)
postulates an origin of of cosmic rays from acceleration
of ions sputtered off dust grains in supernova ejecta by shocks within a
superbubble.
Thus the composition of cosmic rays is more or less constant and they
dominate light element production at early times in the way suggested by
Duncan, Lambert & Lemke.
O/H)
with diminishing metallicity.
(1)
There are also
energetic problems with the production by interstellar spallation at low
metallicity
(Ramaty et al. 1997).
Thus various inhomogeneous processes have been proposed,
beginning with the hypothesis of
Duncan, Lambert & Lemke
(1992)
that fast CNO nuclei in primary cosmic rays are reponsible, and that their
abundance is dominated
by supernova ejecta rather than the interstellar medium. A more detailed
model by
Ramaty & Lingenfelter
(1999)
postulates an origin of of cosmic rays from acceleration
of ions sputtered off dust grains in supernova ejecta by shocks within a
superbubble.
Thus the composition of cosmic rays is more or less constant and they
dominate light element production at early times in the way suggested by
Duncan, Lambert & Lemke.
1 With the large increase in O/Fe claimed by
Israelian et al. and Boesgaard et al. there could be some semblance of
secondary behaviour of the light elements after all, along with iron,
magnesium, calcium etc;
the likelihood of this depends on how the oxygen debate comes out.
Back.
3. ELLIPTICAL GALAXIES
Most of our information on E-galaxies comes from colours and spectral
features of integrated light interpreted with the aid of population
synthesis models based on
the theory of stellar evolution and a spectral library. A classical
result is the correlation between the Lick Mg2 index and
central velocity dispersion
(Bender 1992).
For an old population, Mg2 should be a good measure of the
overall heavy-element abundance Z, dominated by oxygen and other
 -elements,
because Mg itself is one of these and Mg and Si supply 2/3 of the free
electrons providing H- opacity in red-giant
atmospheres. However, age is a complication
and the correlation with iron is more problematic (cf.
Figure 5). At face value,
based on single stellar population (SSP) models by
Worthey (1994) and by
Buzzoni (1995),
the nuclear Z or Mg abundance increases with depth of the potential
well, whereas that of iron does not: the Mg/Fe dilemma. According to
theoretical simulations by
Thomas, Greggio & Bender
(1999)
and Thomas & Kauffmann
(1999),
the expectation would be that star formation goes on for longer in the
bigger E-galaxies, making their weighted-mean age smaller and Mg/Fe
smaller rather than larger.
-elements,
because Mg itself is one of these and Mg and Si supply 2/3 of the free
electrons providing H- opacity in red-giant
atmospheres. However, age is a complication
and the correlation with iron is more problematic (cf.
Figure 5). At face value,
based on single stellar population (SSP) models by
Worthey (1994) and by
Buzzoni (1995),
the nuclear Z or Mg abundance increases with depth of the potential
well, whereas that of iron does not: the Mg/Fe dilemma. According to
theoretical simulations by
Thomas, Greggio & Bender
(1999)
and Thomas & Kauffmann
(1999),
the expectation would be that star formation goes on for longer in the
bigger E-galaxies, making their weighted-mean age smaller and Mg/Fe
smaller rather than larger.
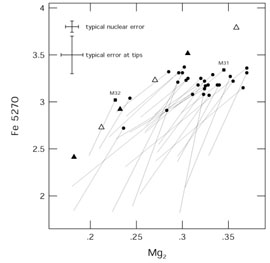
|
Figure 5. Plot of an iron feature against
Mg2. Filled circles and squares
represent the nuclear regions (central 5 arcsec) of elliptical
galaxies, while the sloping lines show the mean trend with
galactocentric distance in each one.
Triangles show model predictions for ages of 9 (solid) and 18 Gyr
(open), based on
SSP models that fit features in globular clusters assuming [Mg/Fe] =
0. A young model with [Fe/H] = 0 fits the nucleus of
M 32 quite well,
and the predicted trends
with metallicity run roughly parallel to several of the observational
lines, but the trend among nuclei is not fitted at all. After
Worthey, Faber &
Gonzalez (1992).
Courtesy Guy Worthey.
|
There is also a "G-dwarf" problem, at least for nuclei, in the sense
that SSP models fit the UV spectra better than those incorporating
simple models of galactic chemical evolution
(Bressan, Chiosi &
Fagotto 1994;
Worthey, Dorman & Jones
1996;
Greggio 1997).
One suggestion has been that the nuclei are pre-enriched with processed
infalling material during a rapid clumpy collapse
(Greggio 1997).
The "concentration model" of
Lynden-Bell (1975)
may also be relevant to this situation, but according
to Worthey, Dorman & Jones this is not just a nuclear problem.
Some notable results emerge from the recent study by
Jørgensen (1999)
of spectral features of galaxies in the Coma cluster. She confirms the
existence of an age-metallicity relation as envisaged in the numerical
simulations of
Thomas & Kauffmann
(1999),
both for iron and magnesium,
consistent with the view that galaxies with deep enough potential wells
to hold on to their gas for longer reach higher metallicities. At any
age, the galaxies with the highest velocity dispersions have the highest
metallicity judged from
magnesium, but for iron quite anomalously the opposite is the case,
which makes
one wonder about the calibration. Finally, Mg/Fe is independent of age and
increases with velocity dispersion, which is hard to explain on the basis
of the orthodox view of the unaided effects of a time lag for SNIa.
Thomas (1999)
has suggested that galactic nuclei may be affected by sporadic
starbursts with a flat IMF.
The question of the IMF, or at least the yield, is also raised by the
supply of iron and other elements to the X-ray gas in rich clusters of
galaxies. Adapting an argument due to
Renzini et al. (1993),
we can start from the empirical finding of
Arnaud et al. (1992)
that the total mass of iron in the gas is proportional to
the total optical luminosity of the E and S0 galaxies in the cluster
according to
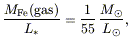
| (1)
|
whence if
M* / L*
 10 solar units, then
10 solar units, then
where the overall true yield
(2)
has been obtained by simply dividing the mass of iron by the
mass of the stars; since the iron: oxygen ratio is about solar, the same
result would have been obtained if we had considered oxygen instead of
iron. This yield, however, is very high in comparison with values of
Z or
slightly less that come up in studies of chemical evolution in the solar
neighbourhood (e.g.
Pagel & Tautvaisiene
1995),
raising the question of whether such a high
value is actually universal and the lesser yields found in other
contexts just a consequence of mass loss from the systems. If so, it
would be sufficient to
enrich the intergalactic medium to the 1/3 of solar value postulated by
Mushotsky & Loewenstein
(1997).
or
slightly less that come up in studies of chemical evolution in the solar
neighbourhood (e.g.
Pagel & Tautvaisiene
1995),
raising the question of whether such a high
value is actually universal and the lesser yields found in other
contexts just a consequence of mass loss from the systems. If so, it
would be sufficient to
enrich the intergalactic medium to the 1/3 of solar value postulated by
Mushotsky & Loewenstein
(1997).
2 Defined as the mass of newly
synthesised and ejected heavy elements from a generation of stars
divided by the mass remaining in long-lived stars and compact remnants
(Searle & Sargent
1972).
Back.
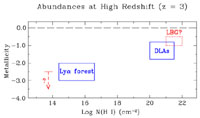
4. ABUNDANCES AT HIGH RED-SHIFT
Naturally recent advances in studies of objects at high red-shift supply
vital clues to the early evolution of galaxies, but, as
Pettini (1999)
has emphasised, our knowledge in this area is severely limited (see
Figure 6), giving rise to serious
observational selection effects. The Lyman forest comes from
condensations in the intergalactic medium, possibly analogues of the
high-velocity H I clouds seen today
(Blitz et al. 1999),
and represents the majority of the baryonic matter in
the universe, while the damped
Lyman- (DLA) systems have a
co-moving density similar to that of disk galaxies today. Then there are
also the Lyman break galaxies, for which there is some information based
on the strength of their
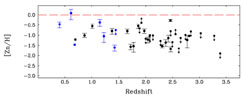
stellar winds. Figure 7 shows the metallicities
of DLA systems, based on zinc abundance, plotted against red-shift, after
Pettini (1999).
When column-density weighted means are formed in distinct red-shift bins,
no evolution is detectable in the metallicity and there
is no obvious way of identifying what sort of objects these systems will
eventually become. Some clues could come from element:element ratios
like N/O or
(DLA) systems have a
co-moving density similar to that of disk galaxies today. Then there are
also the Lyman break galaxies, for which there is some information based
on the strength of their
stellar winds. Figure 7 shows the metallicities
of DLA systems, based on zinc abundance, plotted against red-shift, after
Pettini (1999).
When column-density weighted means are formed in distinct red-shift bins,
no evolution is detectable in the metallicity and there
is no obvious way of identifying what sort of objects these systems will
eventually become. Some clues could come from element:element ratios
like N/O or  /Fe.
Here the difficulty lies in correcting for depletion from the gas phase
on to dust, which can be estimated (when not too large) from the ratio
of Zn to Cr and Fe, since their intrinsic relative abundances are
usually constant. According to
Vladilo (1998)
and Pettini et al.
(1999a,
b),
the resulting relative abundances of
silicon and iron are pretty much solar (or like the Magellanic Clouds
and the "anomalous" halo stars referred to above), suggesting that they
are destined to
become Im galaxies rather than large spirals. The behaviour of N/Si vs
Si/H also shows a resemblance to the behaviour of N/O vs. O/H in
irregular and blue compact galaxies with perhaps an even greater
scatter around the normal primary-secondary pattern than is found in
irregulars and BCGs
(Lu, Sargent & Barlow
1998).
/Fe.
Here the difficulty lies in correcting for depletion from the gas phase
on to dust, which can be estimated (when not too large) from the ratio
of Zn to Cr and Fe, since their intrinsic relative abundances are
usually constant. According to
Vladilo (1998)
and Pettini et al.
(1999a,
b),
the resulting relative abundances of
silicon and iron are pretty much solar (or like the Magellanic Clouds
and the "anomalous" halo stars referred to above), suggesting that they
are destined to
become Im galaxies rather than large spirals. The behaviour of N/Si vs
Si/H also shows a resemblance to the behaviour of N/O vs. O/H in
irregular and blue compact galaxies with perhaps an even greater
scatter around the normal primary-secondary pattern than is found in
irregulars and BCGs
(Lu, Sargent & Barlow
1998).
What are the consequences of the new star formation rate density
(Fig 1) for "metal"
production and global chemical evolution? To begin with, the SFR which I
shall call
 *(conv.) is based on the rest-frame UV
luminosity density combined with a Salpeter power-law IMF between 0.1 and
100 M
*(conv.) is based on the rest-frame UV
luminosity density combined with a Salpeter power-law IMF between 0.1 and
100 M . The
co-moving metal
production-rate density is then usually deduced by dividing by the magic
number of 42 (shades of The Hitch-Hiker's Guide to the
Galaxy), which comes from models of supernova yields in the range
of 10 to 100 M
. The
co-moving metal
production-rate density is then usually deduced by dividing by the magic
number of 42 (shades of The Hitch-Hiker's Guide to the
Galaxy), which comes from models of supernova yields in the range
of 10 to 100 M or so, and I shall call this metal production rate
or so, and I shall call this metal production rate
 Z(conv.). The overall yield then amounts to
Z(conv.). The overall yield then amounts to
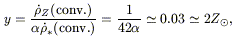
| (3)
|
where 
 0.7 is the lock-up
fraction. Such a high yield is excessive
for the solar neighbourhood (although it may be suitable for
intra-cluster gas)
and so people modelling Galactic chemical evolution generally either use
a steeper
slope, a smaller lower mass limit or assume that stars above 40 or 50
M
0.7 is the lock-up
fraction. Such a high yield is excessive
for the solar neighbourhood (although it may be suitable for
intra-cluster gas)
and so people modelling Galactic chemical evolution generally either use
a steeper
slope, a smaller lower mass limit or assume that stars above 40 or 50
M lock the bulk of their element production in black holes. So the true
rate of "metal" production should be
lock the bulk of their element production in black holes. So the true
rate of "metal" production should be

 Z(conv.), where
Z(conv.), where

 1 is
some correction factor depending on your favourite model of galactic
chemical evolution. Finally, the true star formation rate density should
be corrected by
some factor
1 is
some correction factor depending on your favourite model of galactic
chemical evolution. Finally, the true star formation rate density should
be corrected by
some factor  , also
, also
 1, for the undoubted flattening
of the IMF power law somewhere below
1 M
1, for the undoubted flattening
of the IMF power law somewhere below
1 M , e.g.
Fukugita, Hogan &
Peebles (1998)
have
, e.g.
Fukugita, Hogan &
Peebles (1998)
have  = 0.65, but this does
not influence the conversion factor (at least
to first order) because it is mainly just the massive stars that produce
both the metals and the UV luminosity.
= 0.65, but this does
not influence the conversion factor (at least
to first order) because it is mainly just the massive stars that produce
both the metals and the UV luminosity.
With these preliminaries, we can use the data supplied by
Pettini (1999)
to draw up the following inventory of stars and metals for the present
epoch and for a red-shift of 2.5, assuming
 = 0.67,
= 0.67,
 = 0.65.
= 0.65.
Table 1. Inventory of stars and metals at
z = 0 and z = 2.5
|
|
| z = 0
| z = 2.5
|
|
 *
= *
= 


 *(conv.) dt *(conv.) dt
| 3.6 × 108
M Mpc-3
Mpc-3
| 9 × 107
M Mpc-3
Mpc-3
|
 *
= *
=  * /
7.7 × 1010 h502 * /
7.7 × 1010 h502
| .0047h50-2
| .0012h50-2
|
 *(FHP 98) *(FHP 98)
| .0049h50-1
|
|
 Z
= y Z
= y
 *
= *
=   * /
(42 * /
(42
 ) )
| 2.0 × 107
 M
M Mpc-3
Mpc-3
| 5 × 106
 M
M Mpc-3
Mpc-3
|
 Z (predicted) Z (predicted)
| 2.6 × 10-4
 h50-2
h50-2
| 6.5 × 10-5
 h50-2
h50-2
|
 Z (stars,
Z = Z Z (stars,
Z = Z ) )
| 1.0 × 10-4
h50-1
|
|
 Z (hot gas,
Z =
0.3Z Z (hot gas,
Z =
0.3Z ) )
|
1.7 × 10-4h50-1.5
|
|
|
|
-> 0.4 

 1 1
|
|
 Z (DLA,
Z =
0.07Z Z (DLA,
Z =
0.07Z ) )
|
| 3 × 10-6
h50-1
|
 Z (Ly. forest,
Z =
0.003Z Z (Ly. forest,
Z =
0.003Z ) )
|
| 4 × 10-6
h50-2
|
 Z (Ly. break gals,
Z =
0.3Z Z (Ly. break gals,
Z =
0.3Z ) )
|
| ?
|
 Z (hot gas) Z (hot gas)
|
| ?
|
|
The z = 0 column shows a fair degree of consistency. We can live
with  = 1
if we wish to explain a metal content of intergalactic gas as high as
suggested by Mushotzky & Loewenstein, or we can take this as a firm
upper limit because we do not
know if there is that much "metal" in intergalactic gas.
= 1
if we wish to explain a metal content of intergalactic gas as high as
suggested by Mushotzky & Loewenstein, or we can take this as a firm
upper limit because we do not
know if there is that much "metal" in intergalactic gas.
Somewhat more troubling questions arise at red-shift 2.5, however, as
Pettini (1999)
has already pointed out. It now seems that about a quarter of the stars
have already been formed by then (in ellipticals, bulges and
thick disks?), but known entries in the table only account for 10 per
cent of the
resulting metals (if  = 1) or
25 per cent (if
= 1) or
25 per cent (if  = 0.4). This
is a good
measure of the incompleteness in our knowledge of the distribution of
the elements at substantial red-shifts.
= 0.4). This
is a good
measure of the incompleteness in our knowledge of the distribution of
the elements at substantial red-shifts.
I thank Max Pettini for supplying data and for enlightening discussions.
REFERENCES
Arnaud, M., Rothenflug, R., Boulade, O., Vigroux, L. &
Vangioni-Flam, E.
1992, AA, 254, 49
Balachandran, S.C. & Bell, R.A.
1998, Nature, 392, 791
Beers, T.C., Rossi, S., Norris, J.E., Ryan, S.G., Molaro, P. &
Rebolo, R. 1998, in
Primordial Nuclei and their Galactic
Evolution, N. Prantzos,
M. Tosi & R. von Steiger (eds.), Sp. Sci. Rev., 84, 139
Bender, R. 1992, in IAU Symp. no. 149,
Stellar Populations of Galaxies,
B. Barbuy & A. Renzini (eds.), Kluwer, Dordrecht, p. 267
Blitz, L. 1999, in IAC Euroconference:
The Evolution of Galaxies on
Cosmological Timescales, J.E. Beckman & T.J. Mahoney (eds.),
ASP Conf. Series, in press
Boesgaard, A., King, J.R., Deliyannis, C.P. & Vogt, S.S.
1999, AJ, 117, 492
Bonifacio, P. & Molaro, P.
1997, MNRAS, 285, 847
Bressan, A., Chiosi, C. & Fagotto, F.
1994, ApJS, 94, 63
Buzzoni, A.
1995, ApJS, 98, 69
Cen, R. & Ostriker, J.P.
1999, ApJ, 514, 1
Duncan,D., Lambert, D.L. & Lemke, M.
1992, ApJ, 401, 584
Eggen, O.J., Lynden-Bell, D. & Sandage, A.R.
1962, ApJ, 136, 748
Fuhrmann, K.
1998, AA, 338, 161
Fukugita, M., Hogan, C.J. & Peebles, P.J.E.
1998, ApJ, 503, 518
Fulbright, J.P. & Kraft, R.P.
1999, AJ, 118, 527
Gratton, R., Carretta, E., Matteucci, F. & Sneden, C.
1996, preprint
Greggio, L.
1997, MNRAS, 285, 151
Hartwick, F.D.A.
1976, ApJ, 209, 418
Israelian, G., García Lopez, R.J. & Rebolo, R.
1998, ApJ, 507, 805
Jørgensen, I.
1999, MNRAS, 306, 607
Levshakov, S., Tytler, D. & Burles, S. 1998,
astro-ph/9812114, AJ, subm.
Lu, L., Sargent, W.L.W. & Barlow, T.A.
1998, AJ, 115, 55
Lynden-Bell, D.
1975, Vistas in Astr, 19, 299
McWilliam, A.
1997, ARAA, 35, 503
Madau, P., Ferguson, H.C., Dickinson, M.E. et al.
1996, MNRAS, 283, 1388
Mushotzky, R.F. & Loewenstein, M.
1997, ApJ, 481, L63
Nissen, P.E. & Schuster, W.A.
1997, AA, 326, 751
Pagel, B.E.J. 2000, Phys. Rep., in press
Pagel, B.E.J. & Tautvaisiene, G.
1995, MNRAS, 276, 505
Pagel, B.E.J. & Tautvaisiene, G.
1998, MNRAS, 299, 535
Pettini, M. 1999, in ESO Workshop:
Chemical Evolution from Zero to High
Redshift, J. Walsh & M. Rosa (eds.), Springer-Verlag, in press,
astro-ph/9902173
Pettini, M., Ellison, S.L., Steidel, C.C. & Bowen, D.V.
1999a, ApJ, 510, 576
Pettini, M., Ellison, S.L., Steidel, C.C., Shapley, A.E. & Bowen,
D.V. 1999b, preprint
astro-ph/9910131,
ApJ, in press
Ramaty, R., Kozlovsky, B., Lingenfelter, R. & Reeves, H.
1997, ApJ, 488, 730
Ramaty, R. & Lingenfelter, R. E. 1999, in
LiBeB, Cosmic Rays, and Related X- and
 -Rays,
R. Ramaty,
E. Vangioni-Flam, M. Cassé & K. Olive (eds.),
ASP Conf. Series, Vol. 171, p. 104
Rauch, M., Miralda-Escudé, J., Sargent, W.L.W. et al.
1998, ApJ, 489, 7
Renzini, A., Ciotti, L., D'Ercole, A. & Pellegrini, S.
1993, ApJ, 419, 52
Rich, R.M. 1999, in
Chemical Evolution from Zero to High Red-shift, J. Walsh
& M. Rosa (eds.), Springer-Verlag, in press
Ryan, S., Norris, J. & Beers, T.C.
1996, ApJ, 471, 254
Searle, L. & Sargent, W.L.W.
1972, ApJ, 173, 25
Steidel, C.C., Adelberger, K.L., Giavalisco, M., Dickinson, M. &
Pettini, M. 1999, ApJ, in press,
astro-ph/9811399
Stephens, A.
1999, AJ, 117, 1771
Thomas, D. 1999, MNRAS, in press,
astro-ph/9901226
Thomas, D., Greggio, L. & Bender, R.
1999, MNRAS, 302, 537
Thomas, D. & Kauffmann, G. 1999, in
Spectrophotometric Dating of Stars
and Galaxies, I. Hubeny, S.Heap & R. Cornett (eds.), ASP
Conf. Series,
astro-ph/9906216
Tsujimoto, T. & Shigeyama,
1998, ApJL, 508, L151
Tsujimoto, T., Shigeyama, & Yoshii, Y. 1999, ApJL, in press,
astro-ph/9905057
Vladilo, G.
1998, ApJ, 493, 583
Worthey, G.
1994, ApJS, 95, 107
Worthey, G., Dorman, B. & Jones, L.A.
1996, AJ, 112, 948
Worthey, G., Faber, S.M. & Gonzalez, J.J.
1992, ApJ, 398, 69
-Rays,
R. Ramaty,
E. Vangioni-Flam, M. Cassé & K. Olive (eds.),
ASP Conf. Series, Vol. 171, p. 104
Rauch, M., Miralda-Escudé, J., Sargent, W.L.W. et al.
1998, ApJ, 489, 7
Renzini, A., Ciotti, L., D'Ercole, A. & Pellegrini, S.
1993, ApJ, 419, 52
Rich, R.M. 1999, in
Chemical Evolution from Zero to High Red-shift, J. Walsh
& M. Rosa (eds.), Springer-Verlag, in press
Ryan, S., Norris, J. & Beers, T.C.
1996, ApJ, 471, 254
Searle, L. & Sargent, W.L.W.
1972, ApJ, 173, 25
Steidel, C.C., Adelberger, K.L., Giavalisco, M., Dickinson, M. &
Pettini, M. 1999, ApJ, in press,
astro-ph/9811399
Stephens, A.
1999, AJ, 117, 1771
Thomas, D. 1999, MNRAS, in press,
astro-ph/9901226
Thomas, D., Greggio, L. & Bender, R.
1999, MNRAS, 302, 537
Thomas, D. & Kauffmann, G. 1999, in
Spectrophotometric Dating of Stars
and Galaxies, I. Hubeny, S.Heap & R. Cornett (eds.), ASP
Conf. Series,
astro-ph/9906216
Tsujimoto, T. & Shigeyama,
1998, ApJL, 508, L151
Tsujimoto, T., Shigeyama, & Yoshii, Y. 1999, ApJL, in press,
astro-ph/9905057
Vladilo, G.
1998, ApJ, 493, 583
Worthey, G.
1994, ApJS, 95, 107
Worthey, G., Dorman, B. & Jones, L.A.
1996, AJ, 112, 948
Worthey, G., Faber, S.M. & Gonzalez, J.J.
1992, ApJ, 398, 69
 systems at high
red-shift, which offer rather little evidence
for pure SNII synthesis such as is found in the Galactic halo stars. A
recent estimate of past star formation rates as a function of red-shift
is presented
and the appropriateness of the conventional conversion factor of 42 from
SFR to metal production is discussed. For any reasonable value of this
conversion factor, it is clear that most of the metals existing at
z = 2.5 have yet to be detected.
systems at high
red-shift, which offer rather little evidence
for pure SNII synthesis such as is found in the Galactic halo stars. A
recent estimate of past star formation rates as a function of red-shift
is presented
and the appropriateness of the conventional conversion factor of 42 from
SFR to metal production is discussed. For any reasonable value of this
conversion factor, it is clear that most of the metals existing at
z = 2.5 have yet to be detected.
 INTRODUCTION
INTRODUCTION

 B
h702
B
h702
 0.0035
(
0.0035
( (
(



 O/H)
with diminishing
O/H)
with diminishing 
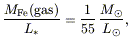
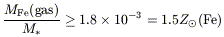
 *(conv.) is based on the rest-frame UV
luminosity density combined with a Salpeter power-law IMF between 0.1 and
100 M
*(conv.) is based on the rest-frame UV
luminosity density combined with a Salpeter power-law IMF between 0.1 and
100 M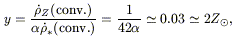

 , also
, also
 *
=
*
= 