Annu. Rev. Astron. Astrophys. 1984. 22: 471-506 Copyright © 1984 by Annual Reviews. All rights reserved

2. INFERENCES INSENSITIVE TO DETAILED MODEL

2.1 Some Fiducial Numbers

Before focusing on specific properties of black holes, it is interesting to consider some general features of compact ultraluminous sources. Certain order-of-magnitude quantities are involved in any model.

A central mass M has a gravitational radius

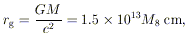
(1)

where M₈ is the mass in units of 10⁸ M. The characteristic minimum time scale for variability is

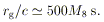
(2)

A characteristic luminosity is the "Eddington limit," at which radiation pressure on free electrons balances gravity:

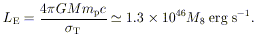
(3)

Related to this is another time scale (112):

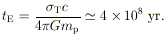
(4)

This is the time it would take an object to radiate its entire rest mass if its luminosity were L_E. The characteristic blackbody temperature if luminosity L_E is emitted from radius r_g is

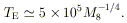
(5)

We can further define a characteristic magnetic field, whose energy density is comparable with that of the radiation. Its value is

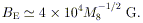
(6)

The expected field strengths induced by accretion flows can be of this order. The corresponding cyclotron frequency is

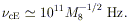
(7)

The Compton cooling time scale for a relativistic electron of Lorentz factor _e (equivalent to the synchrotron lifetime in the field B_E) is

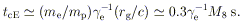
(8)

The photon density n within the source volume is ~ (L/r²c) / <h>. If a luminosity f L_E emerges in photons with h m_e c², which can interact (with a cross section ~ _T) to produce electron-positron pairs (40), then these photons will interact before escaping if

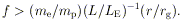
(9)

Several inferences now follow about the radiation processes, given only the assumption that a primary flux with L L_E is generated within radii a few times r_g:

1. Thermal radiation from optically thick material would be in the far-ultraviolet or soft X-ray region; if, however, thermal gas in the region were hot enough to emit X-rays, reabsorption would be unimportant.

2. If the bulk of the luminosity L were synchrotron radiation in a field B B_E (Equation 6), then the self-absorption turnover would be (99)

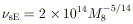
   (10)

   (i.e. typically in the infrared). No significant radio emission can come directly from r r_g unless some coherent process operates at _cE. Synchrotron emission at ~ _sE would require electrons with _e 40M₈^1/14.

3. The synchrotron or inverse Compton lifetimes of relativistic electrons is << (r_g/c) under these conditions, so in any model involving such mechanisms, the radiating particles must be injected or repeatedly reaccelerated at many sites distributed through the source volume.

4. If a substantial fraction of the radiation were generated as gamma rays with energies 1 Mev, then electron-positron pairs would inevitably be produced.

This last point is less familiar than the previous three, and so it may merit some elaboration. Photons with energies above 0.5 Mev will experience an optical depth to pair production that exceeds unity whenever (Lf /r) exceeds a value equivalent to ~ 5 × 10²⁹ erg s^-1 cm^-1. Moreover, the annihilation rate constant for these pairs is ~ _Tc if they are subrelativistic, and smaller by ~ _e² if they are ultrarelativistic (104). This has the important consequence that a compact source that produces gamma rays (either thermally or nonthermally) at a steady rate satisfying (9) will shroud itself within an optically thick "false photosphere" of electron-positron pairs, which scatters and Comptonizes all lower-energy photons (58).

2.2. Processes in Ultrahot Thermal Plasma

The only quantities entering into the above discussion have been essentially those involving the electromagnetic energy densities. We now consider the physical conditions in plasma near a collapsed object. If thermal plasma can radiate efficiently enough, it can cool (even at r r_g) to the relatively modest temperature T_e (Equation 5). However, two-body cooling processes can be inefficient at low densities; for this reason, and also because the energy available in the relativistically deep potential well may amount to 100 Mev ion^-1, the plasmas in AGNs may get hotter than those familiarly encountered elsewhere (even by astrophysicists).

At ion temperatures up to, say, kT_i = 100 Mev the ions are of course nonrelativistic, but the thermal electrons may be relativistic. The main distinctive effects arise because the time scale for establishing electron-ion equipartition via two-body processes, or even for setting up a Maxwellian distribution among the electrons themselves, may exceed the time scale for radiative cooling via the same two-body effects. Moreover, other cooling processes may hold the electron temperature to 1 Mev even if the ions are much hotter. Detailed discussions of these various time scales are given by Gould (54 - 56) and Stepney (121).

COMPTONIZATION     If photons of energy hv are scattered by electrons with temperature T_e such that kT_e >> h, then there is a systematic mean gain (67, 125) in photon energy of ( / ) (kT_e/m_ec²) until, after many scatterings, a Wien law is established. If soft photons are injected in an optically thick (_T > 1) source, then the emergent spectrum depends essentially on the parameter y = _T²(kT_e / m_ec²) : if y << 1, nothing much happens; if y >> 1, a Wien law is set up; but in the intermediate case when y 1, the emergent spectrum has an approximate power-law form. When kT m_e c², the energy change in each scattering is too large for a diffusion approximation to be valid, and Monte Carlo methods are needed (57).

Table 1. Main production/anihilation processes for electron energies > 0.5 Mev

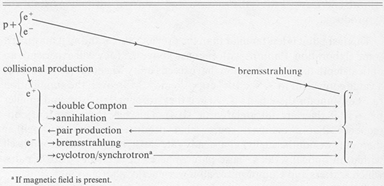
PAIR PRODUCTION EFFECTS     When the electron energies on the tail of the Maxwellian distribution exceed a threshold of 0.5 Mev, collisional processes can create not only gamma rays but also e⁺e^- pairs. These pairs then themselves contribute to the cooling and opacity; the physical conditions must therefore be computed self-consistently, with pairs taken into account (22). Discussions have been given by several authors (22, 40, 69, 70, 132).

The main production/annihilation processes are summarized in Table 1. Further high-energy processes can operate above 50 Mev (46). The fullest discussions of thermal balance in relativistic plasma that take pairs into account are due to Lightman and collaborators (7, 69, 70) and Svensson (122 - 124). There is a maximum possible equilibrium temperature, of order 10 Mev; but if the heat input is raised beyond a certain value, the increment in pair density is so great that the temperature falls again toward 1 Mev. Note that to extend the usual cooling function (T_e) into the temperature range where pair production is important, one must specify the column density n_ir of the source as a second parameter (n_i being the ion density). When n_ir << 1, the dominant pair production is via e-p collisions; but for sources of higher column density, relation (9) may be fulfilled, and more pairs come from + encounters.

2.3. Cyclotron/Synchrotron and Inverse Compton Cooling

Suppose that the magnetic energy is q times the rest mass density of the plasma: we might expect q kT_i / m_p c² for accretion flows. The ratio of the cyclotron cooling time (neglecting reabsorption) to the bremsstrahlung time for a subrelativistic electron is _f(m_e / m_p) q^-1(kT_e / m_e c²)^-1/2, which is << 1 for a plasma with kT_i 1 Mev with an equipartition field; for ultrarelativistic electrons the dominance of synchrotron losses over bremsstrahlung is even greater. Analogously, Compton losses can be very important: indeed, in any source where Thomson scattering on electrons (or positrons) yields _T > 1, the requirement that the Compton -parameter be 1 implies that the electrons or positrons must be mostly subrelativistic.

The conventional distinction between thermal and nonthermal particles becomes somewhat blurred in these contexts where two-body coupling processes cannot necessarily maintain a Maxwellian distribution. Various acceleration mechanisms (relativistic shocks, reconnection, etc.) may, moreover, boost some small fraction of the particles to high : such mechanisms operate in many contexts in high-energy astrophysics and should be even more efficient in an environment where the bulk velocities and Alfvén speeds are both ~ c. These particles would then emit synchrotron or inverse Compton radiation. Such acceleration would be "impulsive," in the sense that its time scale is << r_g / c. The accelerating force would be eE, where E( B) is the electric field "felt" by the charge. There is then a characteristic peak energy attainable by such processes (39), namely that for which the radiative drag due to synchrotron and inverse Compton emission equals eB. For B = B_E (Equation 6), this yields _drag = 4 × 10⁵ M₈^1/4. For acceleration along straight field lines, synchrotron losses are evaded, and the terminal energy could be ~ B_Er_g (corresponding to _e = 3 × 10¹⁴M₈^1/2) if linear acceleration operated over the whole scale of the source. Such limiting energies have emerged from specific studies of accretion disk electrodynamics (34, 72). However, inverse Compton losses cannot be evaded in this way, and they would set a limit not much greater than _drag. (Individual ions, not subject to radiative losses, could in principle get more energetic than electrons.) The parameter _drag scales as B^-1/2, and electrons with this energy emit synchrotron photons with h _f^-1 m_e c² (i.e. 60 Mev) (58, 99). Inverse Compton radiation from the same electrons could of course have photon energies right up to _drag m_e c². There is thus no reason why a (power-law?) spectrum should not extend up to the gamma-ray band.