Annu. Rev. Astron. Astrophys. 1984. 22: 471-506 Copyright © 1984 by Annual Reviews. All rights reserved

3. RADIAL ACCRETION FLOWS

The plasma around black holes will be in some dynamical state - participating in an accretion flow, or perhaps in a wind or jet. Realistically, it would probably be very inhomogeneous: a "snapshot" might reveal many dense filaments at T T_E, embedded in ultrahot thermal plasma filling most of the volume, as well as localized sites where ultrarelativistic electrons are being accelerated. But it is a basic prerequisite for modeling to know how the various cooling and microphysical time scales compare with the dynamical time at a radius r ( r_g). The latter can written as

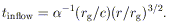
(11)

The parameter , equal to one for free-fall, is introduced explicitly at this stage because the numbers all scale straightforwardly to cases (with < 1) where the inflow is impeded by rotation or by pressure gradients. (In deriving these characteristic numbers, we approximate the flow as spherically symmetric: although this is roughly true for thick tori, further geometrical factors obviously enter for thin disks.)

If accretion with efficiency provides the power, the value of needed to supply a luminosity L can be written as _E = (L / L_E) ^-1, where _E = L_E / c². The particle density at radius r corresponding to an inflow rate is

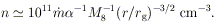
(12)

Another quantity of interest is the Thomson optical depth at radius r, which is

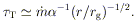
(13)

The "trapping radius," within which an accretion flow would advect photons inward faster than they could diffuse outward [i.e. within which _T > (c / v_inflow)] is

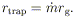
(14)

Note that this depends only on and not on .

In Figure 2 are shown the ratios of various physically important time scales to t_inflow for a radial free-fall with = 1, calculated on the assumption that the ions at each radius are at the virial temperature [i.e. kT_i = m_p c² (r / r_g)^-1]. This assumption is self-consistent because bremsstrahlung cooling and electron-ion coupling are indeed ineffective for = 1. If the magnetic field is close to equipartition, synchrotron cooling is effective for the electrons (except insofar as it is inhibited by self-absorption); Comptonization is important whenever (k T_e / m_e c²) max[, ²] > 1. This diagram helps us to understand the detailed results derived for various specific cases. k

3.1. Spherical Accretion

The specific angular momentum of accreted material is likely to control the flow pattern, especially when close to the hole. Nevertheless, it is worthwhile to start off with the simpler case of spherically symmetric accretion. Some of the quantities derived in this section (for relative time scales, etc.) can, moreover, be straightforwardly scaled to cases where inflow occurs at some fraction of the free-fall speed.

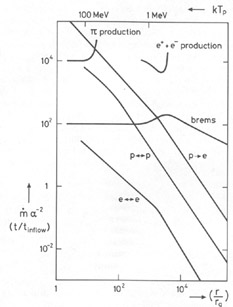
Figure 2. The time scales for various two-body plasma processes are here compared with the inflow time scale for an accretion flow. Processes shown are the self-equilibration time for electrons (e-e) and protons (p-p) (the latter includes nuclear as well as Coulomb effects at > 10 Mev); the time scale for transferring the proton thermal energy to the electrons (p -> e); the bremsstrahlung cooling time for the electrons; and the effects of e+ + e- and production. The proton temperature is taken as the virial temperature [kT = mp c2(r / rg)-1], but the electron temperature is assumed to vary as r-1/2 when the electrons are relativistic. The diagram shows that for free-fall accretion at the "critical" rate ( = 1), two-body cooling processes are inefficient, and the electrons and protons are not thermally coupled by Coulomb interactions when kT > 1 Mev. The ratio of the various time scales to tinflow scales as -1; for inflow at times the free-fall speed, the ratio scales as 2 (for given ). Data on cross sections are from Stepney (121).

If the inflow is laminar, then the only energy available for radiation is that derived from PdV work; therefore, any smooth inflow at high Mach number is certain to be inefficient irrespective of the radiation mechanism. Higher efficiency is possible if the Mach number is maintained at a value of order unity, or if there is internal dissipation (83). However, the fact that the bremsstrahlung cross section is only ~ _{f T} means that this mechanism alone can never be operative on the free-fall time unless >> 1, in which case (from Equation 14) most of the radiation is swallowed by the hole. Several authors have discussed the important effects of Comptonization. If the only photons are those from bremsstrahlung, then merely a logarithmic factor is gained in the radiative efficiency. However, if the magnetic field is comparable with the value corresponding to full equipartition with bulk kinetic energy, then photons emitted at harmonics of the cyclotron frequency can be Comptonized up to energies such that h kT. The most detailed work on this problem is that of Maraschi and collaborators (42, 80): the calculated spectrum is a power law of slope ~ - 1 extending upward from the cyclotron/synchrotron self-absorption turnover to the gamma-ray band.

When a high luminosity L emerges from r r_g, Compton heating or cooling of material at larger r can create important feedback on the flow (45, 92). If the central source emits power L() d at frequencies between + d, then Compton processes tend to establish an electron temperature such that

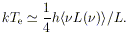
(15)

(This formula strictly applies only if h < m_e c² for all the radiation, and if induced processes can be neglected.) The time scale for this temperature to be established is

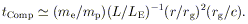
(16)

If t_Comp(r) < t_inflow(r), and if no other heating or cooling processes come into play, the consequences depend on whether kT_e kT_virial = m_p c²(r / r_g)^-1 . If T_e < T_virial, then the inflow must be supersonic, with the pressure support unimportant. Conversely, if there is a range of r where t_Comp < t_inflow but T_e > T_virial, steady inflow is impossible: if the flow were constrained to remain spherically symmetrical, "limit cycle" behavior would develop; but in more general geometry, inflow in some directions could coexist with out-flow in others (18, 19).

A characteristic feature of the region where kT_i >> m_e c² is that the electron-ion coupling time is so long that equality of the electron and ion temperatures is not guaranteed. For low , the collisional mean free paths for each species may exceed r (see Figure 2), though even a very weak magnetic field would suffice to make the inflow fluidlike. However, if there were no such field at all, then each electron or ion could orbit the hole many times between collisions (a situation resembling stellar dynamics around a massive central object): the net inflow velocity would be << c(r / r_g)^-1/2, and the density (and hence the radiative efficiency) would be higher than for the fluidlike free-fall solution with the same value of (85).

Material infalling toward a collapsed object obviously eventually encounters the relativistic domain (51). It is therefore necessary to take note of what general relativity tells us about black holes; this is done in the next section.