Annu. Rev. Astron. Astrophys. 1984. 22: 471-506 Copyright © 1984 by Annual Reviews. All rights reserved

5. ACCRETION FLOWS WITH ANGULAR MOMENTUM

5.1. Origin of Infalling Matter

The accreted material could fall in from the body of the galaxy (gas expelled from ordinary stars via stellar winds and supernovae); it could even come from intergalactic clouds captured by the galaxy. [Relevant here is the evidence that galaxies are more likely to be active if they are interacting with a neighbor (10, 43), and that quasars may be in interacting galaxies (62).] Alternatively, the gas supply may originate in the central parts of the galaxy: e.g. (a) debris from stars tidally disrupted by the hole (60, 61); (b) debris from stellar collisions in a compact star cluster around the hole (52); or (c) a positive feedback process whereby stars are induced to lose mass (and thereby provide further fuel) by irradiation from a luminous central source (82).

The accretion flow pattern depends on the angular momentum of the infalling gas: if this is large and has a steady orientation, then an accretion disk may extend out to very large values of (r/r_g); but the Lense-Thirring effect renders the flow pattern near the hole (where the power is primarily released) insensitive to conditions at large r, provided only that the matter has enough angular momentum to prevent it from falling directly into the hole. Accretion disks have been reviewed by Pringle (101) in a general astronomical context; I summarize here some new developments insofar as they may relate to massive holes in galactic nuclei.

5.2. Thin Disks

The simplest hypothesis is that the central object is being fueled steadily via an accretion disk (35, 73, 117). The standard thin disk model assumes that the gas at each radius is in a nearly Keplerian orbit. Slow radial infall occurs as viscosity transfers angular momentum outward. Energy dissipated by the viscous stress is radiated locally at a rate three times the local rate at which gravitational energy is liberated (GMdr / r between r and r + dr). The factor of 3 arises because viscous stresses transport energy as well as angular momentum outward. This local imbalance is globally rectified in the innermost region of the disk, where the local release of binding energy exceeds the dissipation. For thin disks, slow inflow can be maintained down to the innermost stable orbit; the efficiency then equals the fractional binding energy for this orbit.

A disk has a scale height h normal to the orbital plane such that (h / r) c_s / v_virial, where c_s is the internal sound speed, and is "thin" if this is << 1. One can write

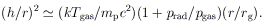
(27)

In this expression, T_gas is the gas temperature in the plane of symmetry (which could significantly exceed the surface temperature if the optical depth were very large); the quantity on the right-hand side is essentially the ratio of thermal and gravitational energies. Generally, the vertical support is provided by gas pressure at large r and for low accretion rates (116). Disks with high are strongly radiation dominated in their inner regions: this is more true when the central hole is supermassive than for a stellar-mass hole because [for a given L / L_E, and thus a given (h / r)] the gas pressure per particle, proportional to T_gas (cf. Equation 5), scales as M^-1/4.

The very simplest models for such disks predict a thermal spectrum typically peaking in the ultraviolet (cf. Equation 5); they thus cannot in themselves account for the very broadband radiation from galactic nuclei. But the major uncertainties in the theory of these disks are the interlinked questions of viscosity and magnetic fields. These fields, amplified by shearing motions (49) and possibly by turbulence-driven dynamo action (102, 103), probably provide the main viscosity. Only crude estimates can be made of the resultant -parameter. Moreover, it is unclear whether the magnetic stresses build up to a fixed fraction of the total pressure or only of the gas pressure. The argument for the latter view (44, 110, 111) is that large-amplitude density contrasts can be induced as soon as magnetic stresses become competitive with gas pressure, and buoyancy effects then elevate the flux into the disk's "corona," impeding further amplification. This can happen, however, only if the radiation is able to diffuse relative to the gas: in the limit of very large optical depths, the field could be amplified by differential rotation on time scales much shorter than those on which density inhomogeneities could develop. Gas and radiation would then act like a single composite fluid, and only the total pressure would be relevant. The answer to this somewhat confusing (though well-posed) theoretical question makes a big numerical difference to the inward drift time scale; more importantly, it determines whether such a disk would be unstable to the "visco-thermal" instability (101).

Magnetic fields may also have a big effect on the radiation spectrum emerging from a realistic thin disk. Energy transported by magnetic buoyancy into a hot corona could dominate the (approximately blackbody) radiation from the dense part of the disk. Magnetic flares in the corona may accelerate relativistic electrons that radiate nonthermally.

Blandford (24) has emphasized that there is no obvious ultimate repository from the angular momentum of disks in galactic nuclei (whereas the companion star and the orbit serve this role for binary star systems). If the magnetic field were sufficiently well ordered, a coronal wind (rather than outward transfer via viscosity within the disk itself) could be the main sink for the angular momentum of accreted material (23, 26). An alternative resolution of the problem, suggested by Ostriker (91), is that the angular momentum is transferred via dynamical friction to a star cluster in which the disk is embedded.

Most of the recent theoretical work on thin disk structure is aimed primarily at understanding cataclysmic variables, X-ray binaries, etc., but it is relevant also in the galactic nucleus context. In all disks, the thermal balance of the outer parts is likely to be controlled by irradiation (causing photoionization, Compton heating, etc.) from the central region. Even where such disks exist, they could be embedded in hotter quasi-spherical structures. There may thus be no clear demarcation in the real world between thin disks and the toroidal structures to which we next turn.

5.3. General Structure of Tori or Thick Disks

Disks become geometrically thick, with h r, if the internal pressure builds up so that c_s (GM / r)^1/2. This can happen either because radiation pressure becomes competitive with gravity or because the material is unable to radiate the energy dissipated by viscous friction, which then remains as internal energy. Before discussing the (very different) internal physical conditions in these two kinds of tori, let us consider their general equilibrium structure.

In thick disks, radial pressure gradients cannot be ignored; the angular velocity is therefore not Keplerian and becomes (within certain constraints) a free parameter. Uncertainty about the viscosity is a major stumbling block. This uncertainty is not crucial to many qualitative features of thin disks (e.g. their overall energetics). However, in thick disks one must deal explicitly with shear stresses in two directions. The stresses determine the distributions both of angular momentum and enthalpy, and therefore the shape of the isobars inside the disk; internal circulation patterns may be important for energy transport. There is always a pressure maximum at r = r_max in the equatorial plane. Outside r_max, the angular velocity is sub-Keplerian, but for r < r_max it is faster than Keplerian. Such structures around Kerr holes were investigated by Bardeen (12) and by Fishbone & Moncrief (50; see also 36, 37). Recent work, from a more astrophysical viewpoint, has been spearheaded by Abramowicz and colleagues (1 - 3, 63, 65, 93, 129). They have exploited an important simplifying feature: the shape of a torus depends only on its surface distribution of angular momentum. If the angular velocity () is given as a function of angular momentum , then the surface binding energy U is given implicitly by

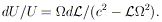
(28)

A simple special case is that for which is the same everywhere. The binding energy is then constant over the whole surface of the torus; there is thus, for each value of , a family of such tori, parametrized by the surface binding energy U. As U tends to zero, the tori "puff up," and the part of the surface close to the rotation axis acquires a paraboloidal shape. The gravitational field is essentially Newtonian throughout most of the volume, but relativistic effects come in near the hole if _min, the angular momentum of the smallest stable orbit. For in the range _min < < ₀, special significance attaches to the torus for which U exactly equals the binding energy of the (unstable) orbit of angular momentum . There is then a cusplike inner edge, across which material can spill over into the hole (just as material leaves a star that just fills its Roche lobe in a binary system). This particular relation between U and would approximately prevail at the inner edge of any torus where quasi-steady accretion is going on (see Figure 3 and caption).

More generally, one can consider (99) tori where goes as some power of . Such tori exist in all cases where the increase of angular momentum with is slower than Keplerian. The funnels tend to be conical rather than paraboloidal if the rotation law is nearer to Keplerian; they extend closer to r = r_g when the black hole is rapidly rotating.

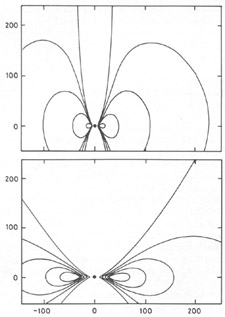
Figure 3. This diagram shows the shape of isobars for tori around a nonrotating (Schwarzschild) hole. The upper picture shows the case = constant in the lower picture, the angular momentum law is -4 (i.e. less different from Keplerian), and the funnels are less narrow. For a given rotation law, narrower funnels (extending inward to smaller r) are possible if the hole is rapidly rotating (J Jmax). The units of length are rg [from Phinney (99)].

Accretion flows where high internal pressures guarantee h r [from (27.)] could resemble such tori if the viscosity parameter were low enough that the flow was essentially circular, and provided also that the configuration were stable (though there is frankly no firm basis for confidence in either of these requirements).

A generic feature of accretion tori is that they are less efficient - in the sense that they liberate less energy per gram of infalling matter - than thin disks. The efficiency is given by the binding energy of the material at the cusp; this depends on the angular momentum profile (via Equation 28), but for an = constant torus of outer radius r₀, it is (r₀ / r_g)^-1, which implies very low efficiency for large tori.

In any torus with r₀ >> r_g and a strongly sub-Keperlian rotation law, rotation is unimportant (gravity being essentially balanced by pressure gradients, and the isobars almost spherical) except near the funnel along the rotation axis. To avoid convective instability, the density must fall off with radius at least as steeply as the isentropic laws

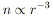
(29)

for = 4/3 (e.g. radiation pressure support), and

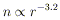
(30)

for = 5/3 (e.g. ion pressure support).

The two very different cases of radiation-supported and ion-supported tori may incorporate elements of a valid model for some classes of galactic nuclei. I discuss them here in turn, and then (in Section 6) I consider another question: whether the "funnels" in such flow patterns are important in collimating the outflowing jet material.

The foregoing discussion begs the question of whether these tori are stable and whether stability requirements narrow down the possible forms for (). Local instabilities can arise from unfavorable entropy and angular momentum gradients (66, 115). These presumably evolve to create marginally stable convection zones, as in a star. Dynamically important magnetic fields may induce further instabilities. Moreover, tori may be seriously threatened by nonaxisymmetric instabilities. Papaloizou & Pringle (94) recently demonstrated that an = constant toroidal configuration marginally stable to axisymmetric instabilities possesses global, nonaxisymmetric dynamical instabilities, which would operate on a dynamic time scale. It is not clear to what extent more general angular momentum distributions are similarly vulnerable, but it may turn out that funnel regions where pressure gradients are balanced by centrifugal effects rather than by gravity are never dynamically stable.

5.4. Radiation-Supported Tori

A thick structure can be supported by radiation pressure only if it radiates at L L_E. Indeed, in any configuration supported in this way, not only the total luminosity but its distribution over the surface is determined by the form of the isobars. Tori with long narrow funnels have the property that their total luminosity can exceed L_E by a logarithmic factor (118). More interestingly, most of this radiation escapes along the funnel, where centrifugal effects make the "surface gravity" (and hence the leakage of radiation) much larger than over the rest of the surface. If accretion powers such a torus, then × (efficiency) 10.

If the outer parts are sufficiently slowly rotating that (29.), or a still steeper law, approximately holds, the characteristic Thomson optical depth must depend on radius r at least as steeply as

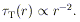
(31)

This in turn implies that the torus cannot remain optically thick (in the sense that _T > 1) out to r >> r_g unless the viscosity parameter at r r_g is very low indeed. (This has been thought by some to be an implausible feature of such models. However, one could argue contrariwise that these objects resemble stars, in which the persistence of differential rotation certainly implies an exceedingly low effective . Pursuing this analogy further suggests that large-scale circulation effects may play as big a role in energy transport as radiative diffusion does.)

If LTE prevails in such a torus, then the temperature at radius r, at locations well away from the rotation axis, is

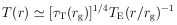
(32)

(cf. Equation 5). The condition for LTE [i.e. that photons can be thermalized within their diffusion time scale _T(r)(r / c)] is more stringent than _T > 1. Indeed, even at the pressure maximum (r r_g), the requirement is

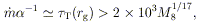
(33)

and radiation pressure dominates gas pressure by a factor of ~ 10⁶ [_T (r_g)]^-1/4 M₈^1/4 - much larger than ever occurs in stellar structure. If _T(r_g) is even larger than (33.), so that LTE prevails out to r >> r_g, the hole may be sufficiently well smothered that all the radiation effectively emerges from a photosphere, in appearance rather like an O or B star (24).

5.5. Ion-Supported Tori

We have seen that for spherically symmetric inflow, the cooling time scale - and even the electron-ion coupling time - can be longer than the free-fall time; the same conditions can prevail even for inflow with angular momentum, provided that is low enough. As compared with Figure 2, all that is changed is that the inflow time is ^-1 t_{free - fall} and the characteristic density for a given is higher by ^-1. The condition for electron-ion coupling to be ineffective in the inner parts of a torus (cf. Figure 2) is

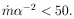
(34)

When (34.) holds, the ions can remain at the virial temperature even if synchrotron and Compton processes permit the electrons to cool, and the disk swells up into a torus. The dominant viscosity is likely to be magnetic. Estimates of magnetic viscosity are very uncertain; Eardley & Lightman (49) suggest that falls in the range 0.01 - 1.0. However, there is no reason why the magnetic should fall as is reduced, so (34.) should definitely be fulfilled for sufficiently low accretion rates.

An accretion flow where is small, and where (furthermore) the radiative efficiency is low, may seem a doubly unpromising model for any powerful galactic nucleus. However, such a torus around a spinning black hole offers an environment where the Blandford-Znajek (29) process could operate (108). Even though it may not radiate much directly, the torus can then serve as a catalyst for tapping the hole's latent spin energy. Three conditions are necessary:

1. Magnetic fields threading the hole must be maintained by an external current system. The requisite flux could have been advected in by slow accretion; even if the field within the torus were tangled, it would nevertheless be well ordered in the magnetosphere. The torus would be a good enough conductor to maintain surface currents in the funnel walls, which could confine such a field within the hole's magnetosphere. The only obvious upper limit to the field is set by the requirement that its total energy should not exceed the gravitational binding energy of the torus. (An equivalent statement is that B should not exceed ^{1/2 -1/2} B_E)

2. There must be a current flowing into the hole. Although an ion-supported torus radiates very little, it emits some bremsstrahlung gamma rays. Some of these will interact in the funnel to produce a cascade (31) of electron-positron pairs (99, 108), yielding more than enough charge density to "complete the circuit" and carry the necessary current - enough, indeed, to make the magnetosphere essentially charge-neutral, in the sense that (n⁺ + n^-) >> |(n⁺ - n^-)|, so that relativistic MHD can be applied.

3. The proper "impedance match" must be achieved between the hole and the external resistance. Phinney (99) has explored the physics of the relativistic wind, whose source is the pair plasma created in the magnetosphere and that flows both outward along the funnel and into the hole. By considering the location of the critical points, he finds consistent wind solutions where ^F is as large as 0.2 ^H. This corresponds (cf. Equation 25) to 60% of the maximum power extraction (for a given B-field). Although some energy is dissipated in the hole, this would still permit a few percent of the hole's rest mass energy to be transformed into a mixture of Poynting flux and a relativistic electron-positron outflow.

The Blandford-Znajek process could operate even if the field threading the hole were anchored to a thin disk, but a thick ion-supported torus provides an attractive model for strong radio galaxies because it could initiate collimated outflow (see the discussion in Section 6). The possibility of such tori depends, however, on the assumption that Coulomb scattering alone couples electrons to ions. This raises the question of whether some collective process might, realistically, be more efficient - if so, the electrons could drain energy from the ions and the torus would deflate. There are bound to be shearing motions, owing to differential rotation, which generate local pressure anisotropies in the plasma. There are certainly instabilities that isotropize the ion plasma, as well as instabilities that isotropize the electron plasma. The key question - which still seems open - is whether these two isotropization processes act almost independently, or whether they can transfer energy from ions to electrons.

[Although electromagnetic extraction of energy is especially important for ion-supported tori (objects where the accretion process is inevitably inefficient), this process could also augment the power generated within a radiation-supported torus. There is in principle no limit to the power that could be extracted from a spinning hole embedded in a dense and strongly magnetized cloud, provided that this power can escape preferentially along the rotation axis without disrupting the cloud. These optically thick radiation-driven jets (21), discussed primarily in the different context of SS 433, could occur in quasars. If the cloud were not sufficiently flattened to permit the excess energy to escape in preferential directions, material would be blown from the cloud, reducing its central pressure: this condition would persist until the total (accretion plus electromagnetic) power fell to L_E, but only a fraction came from accretion.]