4.2. Masses of Clusters
If Newton's laws are valid over intracluster distances, then the virial theorem,
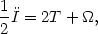
| (8) |
should apply. If, further, a cluster is in a steady state, the polar
moment of inertia should be constant, so
= 0, in which case
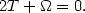
| (9) |
Masses computed for clusters of galaxies are usually based on equation
(9). The requirement
that strictly vanish
does not have to be rigorously fulfilled; if only the cluster
is on the verge of stability, so that the total energy is zero, we
should have
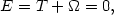
| (10) |
and the mass derived from equation 10 is only a factor of 2 smaller than that obtained from equation (9).
The kinetic energy T can be approximated by
1/2
cl
<V2> , where
cl is the
total cluster mass and
<V2> is the velocity dispersion
weighted by mass. Radial velocities
are usually observed for the brighter and presumably the relatively
massive cluster members; thus little error results from estimating
<V2> from the observed dispersion in
radial velocities in a cluster,
<Vr2> . The
principal uncertainty is that of projection effects.
If the velocity field is isotropic at all points in a cluster, then
<V2> =
<3Vr2> ; if most
galaxies move radially through the cluster, then
<V2> may only slightly exceed
<Vr2> .
The potential energy,
, is
|
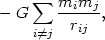
where the summation must be carried out over all pairs of galaxies of
masses mi and mj
separated by distance rij. If the cluster has n
members, there are n(n - 1) / 2
n2/2
such pairs. It is customary to write the potential as - G
cl2
/ 2R', where 1/R' is a
weighted mean of the (1 / rij)'s. Attempts have been
made to evaluate 1 / R' directly for
a few groups, and even for the Hercules cluster (A2151) by the
Burbidges (1959b).
More often,
R' is associated with the apparent radius of a
cluster. For rich symmetrical
regular clusters, the potential can be expressed more conveniently:
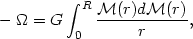
| (11) |
where
(r) is the mass
contained within a radial distance
r of the cluster center. For a
constant mass-to-light ratio, we can write
(r) =
fL(r), which leads to
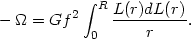
| (12) |
The integral in equation (12) can be evaluated numerically from the density distribution of luminosity in the cluster derived from observations, leading finally to
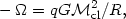
| (13) |
where R is the outer cluster radius and q is a numerical factor that is near unity. For the Coma cluster, for example, Rood (1965), using the writer's observations, finds that q = 0.92. The only unknown in equation (9) (or eq. [10]) is thus the total cluster mass. Setting q = 1, we find
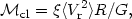
| (14) |
where the factor 
allows for the factor of 2 uncertainty in whether
equation (9) or
equation (10) is more appropriate, and for the projection effects
between <Vr2> and
<V2>;
thus lies in the
range 1/2 to 3.
Although the dynamical method of estimating masses of galaxian clusters
is well known, the assumptions involved have been reviewed here because the
masses found often seem discordant with those estimated from the
luminosities of the cluster members. Ratios of mass to light (in solar
units) found for individual galaxies (e.g.,
Burbidge and Burbidge
1959a) or for double galaxies
(Page 1962)
range from 1 to 15 for spirals and
from 10 to 70 for ellipticals and S0's. On the other hand, to reconcile
the masses
estimated for a number of groups and clusters of galaxies from dynamical
and luminosity
methods, mass-to-light ratios for some of those systems would have to
lie in the range from 100 to 1000 (e.g.,
Limber 1962).
Years ago,
Zwicky (1933), and
Smith (1936)
called attention to the unexpectedly high mass obtained for the
Virgo cluster from its internal kinematics. The
Burbidges (1959b)
have called attention to the same situation
in the Hercules cluster (A 2151). Other discussions of the
problem of
the high dynamical masses found for groups and clusters include those of
de Vaucouleurs (1960),
Burbidge and Burbidge
(1961),
van den Bergh (1961c),
Limber (1961), and
Rood (1965).
The problem, then, is to understand why mass-to-light ratios found for
clusters and groups
of galaxies are often higher - by even a factor of 10 or more - than
those found for individual or double galaxies. Among the possibilities
proposed are the following:
1. Ambartsumian (1958)
has suggested that clusters (at least some of the smaller
groups) have positive energy and are expanding. On the other hand, to
reduce the
dynamical mass of a cluster even by just a factor of 4 from that given
by the virial theorem, we would need to have
T = - 2; in
this case, the observed speeds of galaxies
are, in the mean, only 
2
times greater than the speeds they will have when the cluster
has expanded to infinity. In a period of at most a few times 109
years, all clusters would
dissipate enough to have lost their identity, and it would be difficult
to understand why most galaxies are still in clusters.
2. Perhaps the high masses of some clusters are due to, a few extremely massive galaxies. There does appear to be a tendency for the mass-to-light ratio to be an increasing function of mass for elliptical galaxies (Rood 1965). However, it is very hard to invent convincing stellar populations that can give the extremely high mass-to-light ratios that would be required. Moreover, many of the smaller clusters and groups for which the mass-to-light ratio appears to be high have only spirals among their massive members.
3. The derived mass-to-light ratios are proportional to the assumed value of the Hubble constant. A greatly expanded distance scale would therefore reduce them. But it would also reduce the corresponding ratios found for most individual galaxies and for double galaxies, so the discrepancy would remain.
4. There is a probability that metagalactic structure of larger size than clusters exists i.e., second-order clusters (see next section). If so, and if gravitational forces exist between clusters in such a system, then two or more clusters seen overlapping in projection may occasionally be mistaken for an isolated system, and their relative motions can lead to a spuriously high observed velocity dispersion. In some cases, such an effect may partially be responsible for the mass-to-light discrepancy. The Hercules cluster, in particular, is in a region rich in groups and clusters of about the same distance and may not be a single dynamic unit. De Vaucouleurs's suggestion that the Virgo cluster is at least two clusters has already been mentioned, as has the possibility of inappropriately assuming cluster membership for outlying galaxies in the Coma cluster. In fact, Gott, Wrixon, and Wannier (1973) have shown that some systems that have been identified as groups may actually be optical alignments of field galaxies that are not gravitationally bound at all, and thus that high mass-to-light ratios reported for these systems may be entirely spurious.
5. Subclustering, or incidence of duplicity within a cluster, results in lowering the average separation of galaxies, thereby increasing the potential energy for a given mass. Van den Bergh (1960) has pointed out that binary galaxies in the Virgo cluster can possibly affect significantly the derived cluster mass. Studies of subclustering in several clusters, however (Abell, Neyman, and Scott 1964), show that the phenomenon can not be important generally.
6. A popular explanation is that clusters contain a large amount of invisible matter which adds to their masses but not to their visual luminosities. Zwicky (1957) believes that intergalactic obscuring matter in clusters hides more remote clusters, although the existence of such absorption is not universally accepted. For the Coma cluster, he estimates an obscuration of 0.6 mag (Zwicky 1959). The dust required to produce this absorption, however, corresponds to a density of only 10-30 g cm-3, if the dust has the same obscuring properties as interstellar grains in the Galaxy (de Vaucouleurs 1960); this would be a negligible contribution to the cluster mass. Evidence for luminous haze in the centers of clusters is inconclusive and controversial; if visible luminous matter does exist, it can in no case contribute substantially to the mass of a cluster. Field (1959) has shown that neutral hydrogen cannot be important enough in intergalactic space to affect cluster masses measurably. Observations of the 21-cm line in absorption reported by Robinson, van Damme, and Koehler (1963) suggest the presence of neutral hydrogen in the Virgo cluster, but the total mass indicated is more than two orders of magnitude less than that of the cluster itself. Recent 21-cm observations of three groups by Gott, Wrixon, and Wannier (1973) indicate that neutral hydrogen falls short by at least a factor of 25 of having enough mass to gravitationally bind those systems. Nor is hot plasma likely to be able to contribute appreciably to the potential energies of clusters; an analysis by Davidson, Bowyer, and Welch (1973) of the radio, soft X-ray, and far-ultraviolet observations of the Coma cluster, for example, seems to rule out the possibility that ionized gas contributes enough mass to bind that cluster. Still, intracluster material cannot yet be ruled out in all cases.
Actually, the discrepancy may not be serious for rich
clusters. Luminosities, masses,
and mass-to-light ratios for six relatively rich to rich clusters are
computed from the data
in tables 2 and
6 with equation (14), and are listed in
table 7. The
factor has been set
equal to 2.1, following
Rood's (1970)
analysis of the Coma cluster velocities. The
uncertainty in
can affect a derived cluster mass by at most a
factor of about 2. If, for
example, the clusters have zero energy, so that equation (10) rather
than (9) applies, the actual mass-to-light ratios would be half those
given in table 7. Total radii of 1.2
and 4.0 Mpc are used for the Virgo and Coma clusters, respectively. The
Corona Borealis cluster was also assumed to have a radius of 4.0 Mpc,
and 3.0 Mpc was arbitrarily
chosen for the other clusters, for which the writer has not yet
determined radii observationally.
A Hubble constant of 50 km s-1 Mpc-1 is adopted
throughout. The visual
luminosity is uncertain for cluster 1377, for which only the old
photometry of Baade is
available, but it is probably correct to within a factor of 2; the
velocity dispersion for
this cluster, however, is calculated from only four radial velocities,
so the mass is very
uncertain. For cluster 194, the luminosity was calculated from
magnitudes published by
Zwicky and Humason (1964a;
Abell 1964).
Zwicky and Humason (1964b)
later reported
that some (they do not say which) of the galaxies whose magnitudes they
published
were subsequently discovered not to be cluster members, but it is
doubtful that elimination
of those objects can affect the luminosity given in table 7 by as much
as a factor of 2. The
/ L ratio of
144 found for the Coma cluster can be compared to the value of
about 165 found by
Rood et al. (1972)
(adjusted to the Hubble constant used here).
| Cluster | Mass
= 2.1
( )
| Visual Luminosity, L (solar units) | / L
|
| Virgo | 2.4 × 1014 | 1.3 × 1012 | 181 |
| 194 | 2.4 × 1014 | 3.8 × 1012 | 64 |
| 1377 | 1.9 × 1014 | 2.7 × 1012 | 70 |
| 1656(Coma) | 1.7 × 1015 | 1.2 × 1013 | 144 |
| 2065 (Corona Borealis) | 2.9 × 1015 | 1.2 × 1013 | 231 |
| 2199 (around NGC 6166) | 4.3 × 1014 | 6.1 × 1012 | 71 |
The clusters listed in table 7 are the only rich
ones for which the writer has been
able to find enough data to compute mass-to-light ratios. The ratios
listed are all of the
order 102 or less. For elliptical galaxies in binary systems,
Page (1962)
finds /L
50
(for H = 50 km s-1 Mpc-1). There may still
be a discrepancy of a factor up to 3 because of the uncertainty of
, but this
reexamination of the data shows that a serious mass
discrepancy does not necessarily exist in rich clusters.