4.3. Formation and Evolution of Clusters

It is highly improbable that clusters of galaxies have been built up by chance encounters of galaxies in the general field. Close encounters of three or more bodies of comparable mass can lead to the formation of stable pairs. However, the time required to build a cluster is very great; even if the Universe were old enough (> 10¹² years), most galaxies would still be in the general field rather than in clusters, as the observations suggest. Moreover, if the galaxies in a three-body encounter do not have comparable mass, the energy exchange is too small to produce captures, and observed clusters containing galaxies whose masses range through several orders of magnitude could never be built up by such a process (Ambartsumian 1961). We are nearly forced to conclude, therefore, either that clusters are systems whose member galaxies became gravitationally bound at more or less the same time, or that the clusters represent condensations from pregalaxian material and that subcondensations within them became galaxies.

Many investigators have attempted to determine conditions under which galaxies or clusters can condense from gas or plasma. As yet, there is no successful complete theory for the formation of galaxies and clusters from primordial material. On the other hand, a theory of van Albada (1960, 1961, 1962) gives a rather detailed account of how clusters may form and evolve, given certain initial conditions. His theory is of sufficient interest to warrant a brief review here.

Van Albada assumes that galaxies already existed in a nearly homogeneous expanding universe before the clusters formed. He then considers the conditions under which a region of the expanding universe can become gravitationally unstable. For the sake of mathematical amenability, he considers only spherically symmetrical condensations. For the case of zero cosmological constant, he finds that density fluctuations of only about 2 to 7 percent can lead to gravitational instabilities, which result in the formation of a cluster containing matter originally spread over a region of radius

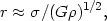
(15)

where is the smoothed-out density of the universe at the time the instability commences, and is the square root of the velocity dispersion. For the latter, van Albada adopts 50 km s^-1. If the radius of the universe is R, varies as R^-3 and as R^-1; thus r varies as R^-1/2. The instabilities, therefore, occur over regions that are relatively smaller as the universe expands. At an early history of the expansion, when R is small, one would expect condensations which would lead to large-scale inhomogeneities, contrary to the cosmological principle. ⁽³⁾ Instabilities must therefore be inhibited somehow at very early epochs, until has decreased to a value of 10^-24 or 10^-25 gm cm^-3; van Albada suggests that radiation pressure might provide this inhibiting force.

With numerical calculations, van Albada follows the growth of an instability and its subsequent evolution. Since the galaxies already exist when the condensation begins, there is no dissipation of kinetic energy by cooling. A central nucleus develops and steadily increases in density and velocity dispersion. Matter streams into the nucleus from a surrounding corona, which in turn attracts matter from the entire unstable region. As the nucleus contracts, the corona changes only slightly. Meanwhile, the expansion of the universe makes the cluster appear relatively more and more prominent against the surrounding field. The density distribution in the inner regions of the cluster is compatible with those observed - for example, with an isothermal polytrope. At no time, however, is the cluster in statistical equilibrium. The condensations develop most slowly from the initial density perturbations of the smallest amplitude. It is possible therefore, that an early instability over a large relative region containing a large mass could begin with a small-amplitude density excess over the mean, and just now be developing into a great cluster. A model of such a system with an age of several billion years has dimensions and structure roughly resembling the Coma cluster.

A point to be remembered is that in the van Albada picture the galaxies exist before clusters form; it is large-scale instabilities in a "fluid" of point-mass galaxies that produce the clusters. Moreover, at early stages the contraction of a cluster is only "contraction" relative to the expanding universe. At later stages the nucleus, as it increases in mass, may contract in an absolute sense, but the increasing velocity dispersion eventually inhibits further contraction and the nucleus expands again. Because the outer layers of the cluster are always expanding absolutely, they cannot stop the expansion of the nucleus, and van Albada expects the cluster ultimately to dissipate. None of his detailed models, however (at the time of writing), have been carried to such an advanced state; in fact, none of them may even correspond to development as advanced as that of actual clusters.

A different approach to the study of the dynamical evolution of clusters is that of Aarseth (1963, 1966, 1969), who begins with a cluster of n members in an arbitrary configuration and with arbitrary initial velocities, and simply solves numerically the "n-body problem." He has considered clusters of from 25 to 100 members, interacting under purely gravitational forces. To take account of the finite sizes of galaxies, Aarseth chooses for the potential function of a galaxy,

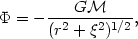
(16)

where is its effective radius.

One of Aarseth's most interesting models, and one which may provide some approximation to an actual cluster of galaxies, has 100 members, distributed initially with a spherically symmetrical density configuration of the form

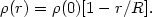
(17)

The 100 objects (representing galaxies) have four different masses: 40 have a relative mass of 0.25; 30 of 0.75, 20 of 1.50, and 10 of 3.75. The complete mass range is thus over a ratio of 15-1. All members are started with random velocities, with the restriction that no object has an initial velocity that will carry it to a greater radial distance from the cluster center than R. In particular, there is no initial correlation between mass and velocity. Aarseth's integration follows the cluster for a period which would correspond in a real galaxian cluster to about 1010 years. During that time, he finds that a nucleus develops which is surrounded by an extended halo. A few of the halo members escape. At the end of the integration period there is a slight radial segregation of members by mass, but the least massive objects have a radial distribution less than 40 percent greater than the most massive ones, and the extreme range in mean kinetic energy, originally over a factor of 15, is reduced by only about half; in other words, the cluster is far from a state of statistical equilibrium. Application of the virial theorem in a naïve way to find the mass of the cluster, however, would lead to a mass error of less than 20 percent. Aarseth finds that about 50 collisions would have occurred in the cluster over the 10¹⁰ years. Only a few stable binary systems are formed, but those have long lifetimes. A similar model cluster with 50 members showed qualitatively similar evolution.

Aarseth also followed the evolution of two irregular model clusters of 50 members each. One was initially V-shaped with its members at rest, and the other had its members spread evenly over an elliptical region, and with small random velocities. In each case a stable "subsystem" formed as a cluster nucleus that retained stability over the entire integration time. Even for these clusters, the mass found from application of the virial theorem would be correct to within 50 percent.

³ The correctness of the cosmological principle has never been observationally verified more than very roughly. Back.