4. CONSEQUENCES OF MASS EXCHANGE

4.1. Mass exchange vs. radiative heating/cooling

When the bulk of the energy content and the bulk of the mass content reside in different phases, a relatively small amount of mass or energy transfer between phases can have a large effect on the structure of a multiphase medium. Such a situation is believed to exist in the three-phase model of the ISM (McKee and Ostriker 1977), where the hot phase occupies most of the volume while most of the mass is in cold clouds. Physically, the effect of mass exchange (either by conduction or ablation followed by effective mixing) is to cool the hot phase, since a fixed amount of energy is being distributed among a larger number of particles. Since radiative heating and cooling depend on both density and temperature, mass exchange can affect the radiative evolution of the medium as well. We can illustrate the global consequences of mass and energy exchange between phases by considering a medium with uniform pressure and subsonic motions, in which mass exchange is driven by thermal conduction. The approximate time-dependent equations governing the medium are then

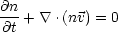
	(10)
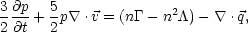
	(11)

where 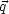represents the conductive heat flux. Note that these equations are appropriate in the single-fluid limit, corresponding to classical or mildly saturated conduction (Cowie and McKee 1977): in the highly saturated suprathermal limit (Balbus and McKee 1982), both the single-fluid approximation and the assumption of pressure balance break down. The evolution of the medium is driven by the terms on the right-hand-side of eq. (11), and may be dominated either by the effects of conduction or by the effects of radiative heating and cooling.

There is a crucial distinction between the heat flux term and the radiative loss term in the energy equation: the energy entering or leaving a volume of radius r due to conduction is proportional to r² q( r for classical conduction) whereas that due to heating or cooling is proportional to r³. Thus, there is a critical length scale which enters the problem, which turns out to be the Field length, _F (eq. [8]), when mass exchange is driven by classical conduction.

The temperature structure of the intercloud medium in a system of clouds extending over a region of size R depends on the ratio of the Field length to R. Balbus (1985) developed an elegant electrostatic analogy for an ensemble of clouds in a hot intercloud medium under conditions in which radiative heating and cooling are negligible and the temperature is specified on the boundary of the ensemble. This corresponds to the case R << _F. In a steady state, the evaporation rate and the temperature structure in the intercloud medium are then determined by a solution of Laplace's equation with Dirichlet boundary conditions. In the complementary case, R >> _F, global heat flows are insignificant and the temperature structure of the intercloud gas is determined by a competition between cloud evaporation on the one hand and heating and cooling on the other. Numerically, the Field length is

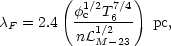
(12)

where T₆ T/10⁶ K and _{M-23 M} / (10^-23 erg cm³ s^-1) is normalized to a characteristic value of the radiative cooling rate for astrophysical plasmas.

To quantify the competition between mass exchange and radiative heating/cooling, consider the spatially averaged effect of cloud evaporation on the hot phase. This is meaningful only when the characteristic temperature of the hot phase changes over a length scale which exceeds the mean intercloud separation r₀. This condition is guaranteed to be satisfied when r₀ is smaller than _F. When r₀ exceeds _F, then mass exchange cannot compete with radiative heating and cooling anyway, so the point is moot. If there are n_cl( 3/4 r³₀) clouds per unit volume evaporating at a mean rate _ev per cloud, then the density of the intercloud medium changes at a rate

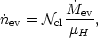
(13)

where _ev is negative for condensation. We may then use 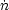_ev to define an effective evaporative cooling rate,

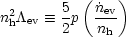
(14)

(Begelman and McKee 1990). The evaporative cooling coefficient _ev is analogous to the radiative cooling coefficient in that both reduce the specific entropy s, but there are crucial differences between the two: reduces the total entropy of a given volume of intercloud gas, whereas _ev increases it; reduces the energy density of the intercloud gas, whereas _ev leaves it unchanged. Because of these distinctions, _ev should not be included in the net radiative cooling function . However, the relative impact of mass exchange and radiative heating/cooling on the thermal state of the intercloud medium can be expressed by the radiation/evaporation ratio (Begelman and McKee 1990),

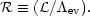
(15)

When _{M M} / _ev is >> 1( << 1), then radiative heating and cooling (mass exchange) determines the thermal state of the intercloud medium.

One can express in terms of quantities which characterize the structure of the two-phase medium. Writing the evaporation rate in the form _ev = 4 r²_{c h} c_sf, where c_s is the isothermal sound speed in the hot phase, we have

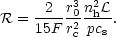
(16)

r₀ may be eliminated in favor of the cloud filling factor f (assumed to be << 1) by substituting r_c/f for r₀³ / r_c². In the limit of saturated evaporation F ~ a few (Cowie and McKee 1977), while F ~ / 4 in the Nulsen (1982) model of ablation. In the classical conduction limit, F is twice the "saturation parameter" '₀ derived by Cowie and McKee (1977), with the result that

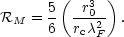
(17)

Cloud evaporation thus determines the intercloud temperature for r_c > r³₀ / _F². The corresponding condition on the filling factor is

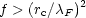
(18)

or f > (r₀ / _F)⁶; for f ~ 0.03, as in the ISM, this will be true if _F 2r₀. In terms of the sound-crossing time across r_c (measured in the hot phase), t_s ~ r_c / 2c_s, and the radiative cooling time in the hot phase, t_c ~ 5kT_h / 2n_h (T_h) , we may express the condition for mass exchange to dominate globally in the form

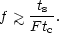
(19)

Writing (18) in the form r₀ < r^1/3_{c F}^2/3, we see that the intercloud spacing in a conduction-dominated medium must also be smaller than the Field length. This has important consequences for the thermal stability of the hot phase in a conduction-dominated system. Since _F is roughly the minimum wavelength which is thermally unstable (Field 1965), potentially unstable regions must contain many clouds. The conduction-modified condition for thermal instability is obtained simply by including _ev in Balbus's (1986a) criterion (eq. [4]):

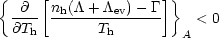
(20)

(Begelman and McKee 1990). n_{h ev} / T_h is generally an increasing function of T_h: for isobaric perturbations n_{h ev} / T_h ~ q T_h^7/2(T_h^1/2) for classical (saturated) conduction. Therefore, evaporation has a stabilizing influence on the hot phase, and in a conduction-dominated medium thermal instability will be inhibited by the presence of evaporating clouds (Begelman and McKee 1990). This will be true even if the radiative processes place the hot phase in a thermally unstable regime. However, it should be noted that the cooling time scale in the hot phase of a conduction-dominated medium is shorter than the radiative cooling time scale. Therefore, conduction cannot stabilize a hot phase over a time scale which is longer than the time scale for radiative thermal instability. However, it can lead to the hot phase cooling down somewhat before the onset of thermal instability. Since thermal conduction generally becomes less important at low temperatures, such a system may evolve to a state in which evaporative cooling no longer dominates, whereupon thermal instability may occur. Since the Field length is generally a strongly increasing function of temperature, the operation of thermal instability may lead to the production of smaller and more closely spaced clouds than would have formed in the hotter medium.

It is instructive to apply the ideas discussed above to the three-phase model of the ISM (McKee and Ostriker 1977). The three-phase ISM consists of cold HI clouds surrounded by warm HI and HII envelopes, all embedded in a pervasive hot ionized medium (HIM). The physical conditions in the HIM are governed by mass exchange with the clouds and energy injection by supernovae. The model is intrinsically time-dependent: A given element of gas is compressed and heated by SNRs at intervals of about 5 × 10⁵ yr, and this makes its evolution difficult to analyze using concepts developed to treat steady-state or slowly evolving systems. Nonetheless, it is of interest to evaluate the Field length and the radiation/evaporation ratio. 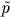Using the fit to the cooling function of Raymond, Cox and Smith (1976) for cosmic abundances, (T) 1.6 × 10^-19T^-1/2 erg cm³ s^-1 (10⁵ K < T < 4 × 10⁷ K), multiplied by an enhancement factor 10₁ 10 to take account of nonequilibrium ionization and density inhomogeneity near conduction fronts (McKee and Ostriker 1977), we have _F = 44(_c^1/2 T³₆ / _{4 1}^1/2) pc, where 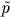₄ p / 10⁴k and T₆ T_h/10⁶ K. We can write condition (18) in the form

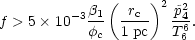
(21)

It is evident that the relative importance of conductive and radiative energy exchange is sensitive to conditions in the hot phase, particularly to T_h, as well as to the filling factor and typical size of clouds. Under the conditions deduced by McKee and Ostriker (T₆ = 0.45, ₄ = 0.36, ₁ = 1, r_c = 2.1 pc, and f = 0.23), condition (21) is marginally satisfied. Equivalently, the radiation/evaporation ratio is given by R = 0.38, which implies that evaporative cooling dominates radiative cooling and that the HIM is thermally stable. (The argument that evaporation can stabilize the HIM is originally due to McCray [1986].) However, even a small amount of cloud ablation by hydrodynamic processes (Section 3.2) or a slight increase in the HIM temperature would lead to a drastic increase in the energetic importance of evaporation. If the typical clouds were sufficiently small that conduction were saturated, i.e., for

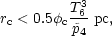
(22)

(Cowie and McKee 1977; Balbus and McKee 1982), the appropriate version of condition (19) would be

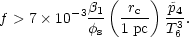
(23)

In the McKee-Ostriker picture, each region of HIM is overrun by another supernova remnant before it has time relax to a stationary state with 1. Stochastic heating by SNR shocks thus leads to discontinuous trajectories in the p - V plane, and heating is balanced by radiative cooling. In the galactic fountain model (Shapiro and Field 1976; Wang and Cowie 1988), the heat is advected into the galactic halo. If clouds are effectively ablated then the accelerated lowering of T_h by evaporation may allow the large tracts of the ISM to cool to a homogeneous state at T 10⁴ K. The intercloud medium remains thermally stable until radiative cooling begins to dominate over evaporative cooling, at T_h 10⁵ K. Since the Field length is a strongly increasing function of T_h, the onset of instability at a reduced temperature may lead to the formation of sub-parsec size clouds.