4.2. Evolution of multiphase systems

By averaging the equations of mass and energy conservation over a volume (V) which contains many clouds, one can derive equations for the global evolution of the hot intercloud medium in the presence of mass exchange with embedded clouds (Begelman and McKee 1990). The mass of intercloud gas in is _h µ_H , where _h is the mean density of the intercloud gas in . Choosing the volume to comove with the intercloud gas implies that this mass can change only by cloud evaporation, at a rate 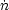_ev µ_H . Mass conservation for the intercloud gas then becomes

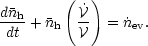
(24)

Integration of equation (11) over then implies

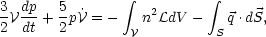
(25)

where s is the surface bounding . By assuming that the characteristic dimension of the averaging volume is large compared to the Field length, we ensure that the conductive heat flux term in equation (25) is negligible compared to the heating and cooling term. The global energy equation then simplifies to

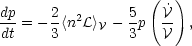
(26)

where < > denotes an average over the volume . Note that mass exchange does not enter this equation: mass exchange alters the density and temperature of the intercloud gas, but not its pressure.

Additional constraints are required to solve for the evolution of a specific system. Since the cloud evaporation rate depends on the typical cloud size, it is necessary to have an equation for the evolution of r_c in time. There are also likely to be externally imposed constraints on the intercloud medium; Begelman and McKee (1990) considered two limiting cases. In the isochoric limit, tile comoving volume is held constant as the system evolves. If one assumes that the clouds are fixed as well, then the mean density also remains constant. This condition would apply in a system in which the sound crossing time R/c_s is long compared to both the characteristic heating/cooling time and the evaporation time. Such a situation might apply locally within a supersonic accretion flow or wind. Setting 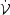= 0 in eqs. (24) and (26), we obtain

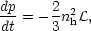
(27)

and

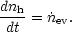
(28)

In the isobaric limit, the intercloud medium can exchange mass with a reservoir in order to maintain a constant pressure, so we set p(t) = constant. Such a situation might apply, for example, if the system were in contact with an X-ray heated wind above an accretion disk (Begelman, McKee and Shields 1983). We then have

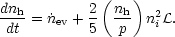
(29)

The instantaneous state of the intercloud medium can be described by the location of a point in the p - V plane (cf. Fig. 1); V n^-1_h is the specific volume of the intercloud gas. The radiative equilibrium curve n²_h = 0 divides the plane into two regions: above the curve, radiative cooling exceeds the external heating, whereas below the curve the converse is true. The net cooling rate n²_h may be assumed to be a known function of p and V everywhere on the plane. However, the evaporation rate 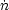_ev also depends on the distribution of cloud sizes and separations.

The character of a trajectory in the p - V plane is determined by the relative importance of energy exchange and mass exchange, which is expressed quantitatively by the radiation/evaporation ratio (eq. [16]). in the isochoric case, the slope of trajectories in the p - V plane is governed by the ratio of equations (27) and (28):

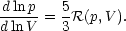
(30)

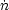Trajectories are nearly vertical if radiative cooling and heating are dominant (|| >> 1), and nearly horizontal if mass exchange is dominant (|| << 1). It is immediately obvious that trajectories must be locally horizontal (dp / dV = 0) where they cross the equilibrium curve ( = 0), provided that _ev 0 at the point of crossing. Points at which = 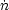_ev = 0 represent stationary states. The temperature evolves as

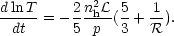
(31)

Trajectories with = - 3/5 are isothermal. Isobaric trajectories are constrained to be horizontal in the p - V plane. The direction (and rate) of motion is given by equation (29), which may be written in the form

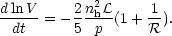
(32)

Since T pV V in the isobaric case, this equation also describes the temperature evolution of the system. The point = - 1 represents a steady state for the hot phase, although mass continues to be lost (if < 0) or gained (if > 0) by clouds in this state (unlike the "true" steady state = _ev = 0 in the isochoric case). For a system dominated by radiative heating or cooling (|| >> 1), evolution is leftward above the thermal equilibrium curve and rightward below the curve. In a system dominated by mass exchange (|| << 1), evolution is leftward for evaporation and rightward for condensation. A more detailed discussion of p - V plane trajectories may be found in Begelman and McKee (1990), who considered the specific case of a gas heated by Compton scattering and cooled by bremsstrahlung and the inverse Compton effect. They also discuss the stability properties of evolving systems.