1.2. Lagrangian and Hamiltonian formulations

The equations of Newtonian cosmology may be derived from Lagrangian and Hamiltonian formulations. The latter is particularly useful for treatments of phase space.

In the Lagrangian approach, one considers the trajectories x() and the action S[x()]. From elementary mechanics (with proper coordinates and no cosmology, yet), S = L dt with Lagrangian L = T - W = 1/2 mv² - m for a particle moving in a potential (T is the kinetic energy and W is the gravitational energy). We now write a similar expression in comoving coordinates, bearing in mind that the action must be a proper quantity:

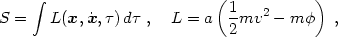(1.8)

where 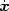= v is the peculiar velocity. We will show that eq. (1.8) is the correct Lagrangian by showing that it leads to the correct equations of motion.

Equations of motion for the trajectories follow from Hamilton's principle: the action must be stationary under small variations of the trajectories with fixed endpoints. Thus, we write x() x() + x(), dx / d dx / d + (d / d)x(). The change in the action is

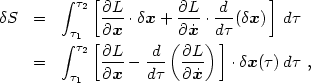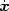where we have integrated by parts assuming (L / ) ^. x = 0 at = ₁ and ₂. Applying Hamilton's principle, S = 0, we obtain the Euler-Lagrange equation (it works in cosmology, too!):

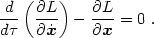(1.9)

The reader may verify that substituting L from eq. (1.8) yields the correct equation of motion (1.7).

It is straightforward to extend this derivation to a system of self-gravitating particles filling the universe. The Lagrangian is

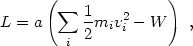(1.10)

where the total gravitational energy excludes the part arising from the mean density:

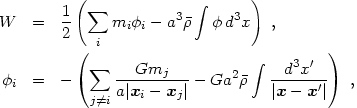(1.11)

where the factor 1/2 is introduced to avoid double-counting pairs of particles. For a continuous mass distribution we obtain

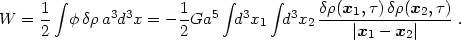(1.12)

In the Hamiltonian approach one considers the trajectories in the single-particle (6-dimensional) phase space, {x(), p()}. The aim is to obtain coupled first-order equations of motion for x() and p(), known as Hamilton's equations, instead of a single second-order equation for x().

The derivation of Hamilton's equations has several steps. First we need the canonical momentum conjugate to x:

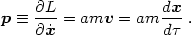(1.13)

Note that p is not the proper momentum measured by a comoving observer: mv is. In Hamiltonian mechanics, one must use the conjugate momentum and not the proper momentum.

The next step is to eliminate dx / d from the Lagrangian in favor of p. We then transform from the Lagrangian to a new quantity called the Hamiltonian, using a Legendre transformation:

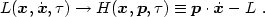(1.14)

Notice that we transform L to H and to p (the latter through eq. 1.13). Why do we perform these transformations? The answer is that now Hamilton's principle gives the desired equations of motion for the phase-space trajectory {x(), p()}. In phase space, Hamilton's principle says that the action S = L d = (p 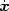^. - H) d must be stationary under independent variations of all phase space coordinates: x() x() + x() and p() p() + p(). As an exercise, the reader can show, using a method similar to the derivation of the Euler-Lagrange equation above,

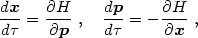(1.15)

provided that p ^. x = 0 at the endpoints of .

In our case, H = p² / (2am) + am (getting the a's right requires using the Legendre transformation), yielding

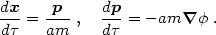(1.16)

These equations could be combined to yield eq. (1.7), but in the Hamiltonian approach we prefer to think of two coupled evolution equations. This is particularly useful when studying the evolution of a system in phase space, as we shall do in section 3 with hot dark matter.