The previous lecture studied the evolution of an ideal collisional gas
including gravity and pressure. A gas of neutrinos, or of collisionless
dark matter particles, behaves differently. In this lecture we investigate
the evolution of a nonrelativistic collisionless gas whose particles
have significant thermal speeds. (Relativistic kinetic theory is
discussed by
Stewart 1971,
Bond & Szalay 1983,
and Ma & Bertschinger
1994b.)
An example is the gas of relic thermal neutrinos that decoupled
at a temperature
kBT ~ 1 MeV in the early universe. The
present number density of these neutrinos (about 113
cm-3 for each
of the three flavors) is such that a single massive type contributes
m
c2 / (93 h2 eV) to
, where
h = H0 / (100 km s-1
Mpc-1). Massive neutrinos are
called hot dark matter because their thermal speeds significantly affect
the gravitational growth of perturbations.
Before working out the detailed equations of motion for hot dark matter, it is useful to consider in general terms the effect of a thermal distribution. Suppose we have a cold gas with no thermal motions. In this case it doesn't matter whether the gas is collisional or collisionless: gravitational instability amplifies the growing mode of irrotational density perturbations. What happens when we add thermal motions? We know the answer for a collisional gas: pressure stabilizes collapse for wavelengths less than the Jeans length, the distance sound waves travel in one gravitational dynamical time. For collisionless particles we also expect suppression. However, a collisionless gas cannot support sound waves, because no restoring force is provided by particle collisions.
A perfect collisional gas is fully described by its mass (or energy) density, fluid velocity, and temperature as functions of position. All other properties follow from the fact that the phase space density distribution is (locally) the thermal equilibrium distribution, e.g. Maxwell-Boltzmann. This is not true for a collisionless gas, whose complete description requires specifying the full phase space density.
For a collisionless gas, the velocity distribution function may be far from Maxwellian, so that the spatial stress tensor is not the simple diagonal form appropriate for an ideal gas. Instead there may be significant off-diagonal terms contributing shear stress that acts like viscosity in a weakly collisional fluid: it damps relative motions. We expect perturbations in a collisionless gas to be damped for wavelengths shorter than the distance traveled by particles with the characteristic thermal speed during one gravitational collapse time, the collisionless analogue of the Jeans length. Stated simply, overdense or underdense perturbations decay because the particles fly away from them at thermal speeds. This collisionless damping process is called free-streaming damping.
The characteristic thermal speed of massive neutrinos after they become nonrelativistic is
 |
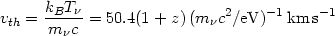(3.1) |
where we have used the standard big bang prediction
T =
(4/11)1/3
T
(e.g.,
Kolb & Turner 1990)
with T
2.735 K
today. Multiplying vth by the gravitational time
(4
G
a2)-1/2 gives the comoving free-streaming
distance,
 |
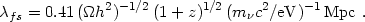(3.2) |
At any time, fluctuations with wavelength less than about
fs
are damped; much longer wavelength fluctuations grow with negligible
suppression.
The free-streaming distance does not really grow without bound as
z 
because the neutrino thermal speed cannot exceed c. Applying this
limit gives a maximum comoving free-streaming distance of
 |
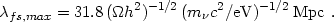(3.3) |
Thus, unless they are regenerated by perturbations in other components (as happens, for example, in a model with hot and cold dark matter), primeval density fluctuations in massive neutrinos with wavelength smaller than this rather large scale will be erased by free-streaming damping. A more quantitative treatment is presented below using the actual evolution equations for the neutrino phase space density distribution.