2.2. Linear instability 1: isentropic fluctuations and Jeans criterion

We begin with some nomenclature from thermodynamics. Isentropic means S = 0: the same entropy everywhere. Adiabatic means dS/d = 0: the entropy of a given fluid element does not change. The two concepts are distinct. It is common in cosmology to say "adiabatic" when one means "isentropic." This usage is confusing and I shall adopt instead the standard terminology from thermodynamics.

Isentropic fluctuations are the natural outcome of quantum fluctuations during inflation followed by reheating: rapid particle interactions in thermal equilibrium eliminate entropy gradients. If S = 0, the linearized fluid and gravitational field equations are

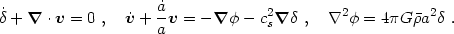(2.11)

Combining these gives a damped, driven acoustic wave equation for :

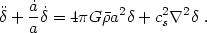(2.12)

Aside from the Hubble damping and gravitational source terms, this equation is identical to what one would get for linear acoustic waves in a static medium.

To eliminate the spatial Laplacian we Fourier transform the wave equation. For one plane wave, (x, ) (k, )exp(ik ^. x). The wave equation becomes

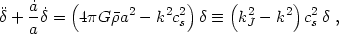(2.13)

where we have defined the comoving Jeans wavenumber,

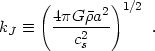(2.14)

Neglecting Hubble damping (by setting a = 1), the time dependence of the solution to eq. (2.13) would be exp(- i ), yielding a dispersion relation very similar to that for high-frequency waves in a plasma, but with an important sign difference because gravity is attractive:

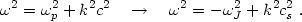(2.15)

The plasma frequency is _p = (4 n_e e² / m_e)^1/2 while the Jeans frequency is _J = k_J c_s = (4 G )^1/2. Whereas electromagnetic waves with ² < _p² do not propagate (k² < 0 implies they are evanescent, e.g., they reflect off the Earth's ionosphere), gravitational modes with k < k_J are unstable (² < 0), as was first noted by Jeans (1902). In physical terms, pressure forces cannot prevent gravitational collapse when the sound-crossing time / c_s is longer than the gravitational dynamical time (G)^-1/2 for a perturbation of proper wavelength = 2a/k.

Including the Hubble damping term slows the growth of the Jeans instability from exponential to a power of time for k << k_J. In general there is one growing and one decaying solution for (k, ); these are denoted _±(k, ). For c_s² = 0 and an Einstein-de Sitter (flat, matter-dominated) background with a() ₂, _{+ 2} and _- ^-3. For k >> k_J, we obtain acoustic oscillations. In a static universe the acoustic amplitude for an adiabatic plane wave remains constant; in the expanding case it damps in general. An important exception is oscillations in the photon-baryon fluid in the radiation-dominated era; the amplitude of these oscillations is constant. (Showing this requires generalizing the fluid equations to a relativistic gas, a good exercise for the student.) In any case, acoustic oscillations suppress the growth relative to the long-wavelength limit.

It is interesting to write the linear wave equation in terms of rather than using ² = 4 Ga² a^-1 for nonrelativistic matter (with c_s² << c²):

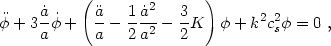(2.16)

where we used the Friedmann equation (1.6); recall that K = ( - 1)(aH)² is the spatial curvature constant. In a matter-dominated universe, differentiating the Friedmann equation gives /a - (1/2)² / a² = - (1/2)K, yielding

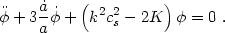(2.17)

When written in terms of the gravitational potential rather than the density, the wave equation loses its gravitational source term.

The solutions to eq. (2.17) depend on the time-dependence of the sound speed as well as on the background cosmology. To get a rough idea of the behavior, consider the evolution of the potential in an Einstein-de Sitter universe filled with an ideal gas. For a constant sound speed, the solutions are

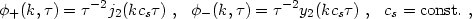(2.18)

where j₂ and y₂ are the spherical Bessel functions of the first and second kinds of order 2. Although simple, this is not a realistic solution even before recombination (in that case, the photons and baryons behave as a single tightly-coupled relativistic gas, and relativistic corrections to the fluid equations must be added), except insofar as it illustrates the generic behavior of the two solutions: (damped) oscillations for kc_s >> 1 and power-law behavior for kc_s << 1.

An alternative approximation, valid after recombination, is to assume that the baryon temperature roughly equals the photon temperature (this is a reasonable approximation because the small residual ionization thermally couples the two fluids for a long time even though there is negligible momentum transfer), c_s² = c_0s² a^-1 where c_0s is a constant. In this case the solutions are powers of :

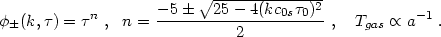(2.19)

The solutions oscillate for kc_s0 > 5/2 and they damp for kc_s0 > 0.

In both of our solutions, and indeed for any reasonable equation of state in an Einstein-de Sitter universe, long-wavelength (kc_s << 1) growing density modes have corresponding potential ₊ = constant, while the decaying density modes have _ a^-3 d. The density perturbation and potential differ by a factor of a² a^-1 from the Poisson equation. If K < 0 or k²c_s² > 0, then ₊ decays with time, although ₊ still grows. Note that the important physical length scale where the transfer function ₊(k, ) / (k, 0) falls significantly below unity is the acoustic comoving horizon distance c_s, not the causal horizon distance c or the Hubble distance c/H. Setting c_s to the acoustic speed of the coupled photon-baryon fluid at matter-radiation equality gives the physical scale at which the bend occurs, c_{s eq}, in the power spectrum of the standard cold dark matter and other models.