2.4. Vorticity - or potential flow?

With the growing and decaying isentropic perturbations, and the isocurvature mode, we have accounted for three of the expected five linear modes. The remaining two degrees of freedom were lost when we took the divergence of the Euler equation, thereby annihilating any transverse (rotational) contribution to v. We consider them now.

Theorem: Any differentiable vector field v(x) may be written as a sum of longitudinal (curl-free) and transverse (divergence-free) parts, v_|| and v, respectively:

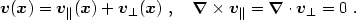(2.22)

The proof follows by construction, by solving ^. v_|| = and × v = where ^. v and × v. In a flat Euclidean space, solutions are given by

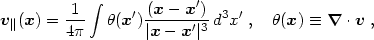(2.23)

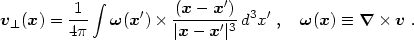(2.24)

Note that this decomposition is not unique; we may always add to v_|| a curl-free solution of ^. v_|| = 0 and to v a divergence-free solution of × v = 0 (e.g., constant vectors). With suitable boundary conditions (e.g., v_|| d³x = 0 when integrated over all space) this freedom can be eliminated. The variables and are called the (comoving) expansion scalar and vorticity vector, respectively.

In our preceding discussion of perturbation evolution we have implicitly considered only v_||. The remaining two degrees of freedom correspond to the components of v (the transversality condition ^. v = 0 removes one degree of freedom from this 3-vector field). Fortunately, we can get a simple nonlinear equation for v - actually, for its curl, - by taking the curl of the Euler equation:

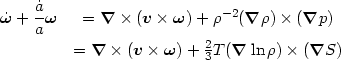(2.25)

where we have assumed an ideal monatomic gas in writing the second form. The term arising from entropy gradients is called the baroclinic term. It is very important for the dynamics of the Earth's atmosphere and oceans (Pedolsky 1987).

An important general result follows from eq. (2.25), the Kelvin Circulation Theorem: If = 0 everywhere initially, then remains zero (even in the nonlinear regime) if the baroclinic term vanishes. (We are assuming that other torques such as magnetic ones vanish too.) The reason for the importance of this result in cosmology is that many models assume irrotational, isentropic initial conditions. With adiabatic evolution, it follows that = 0. Such a flow is also called potential flow because the velocity field may then be obtained from a velocity potential: v = v_|| = - _v.

Nonadiabatic processes (heating and cooling) and oblique shock waves can generate vorticity. In a collisionless fluid, if the fluid velocity is defined as the mass-weighted average of all the mass elements at a point, this averaging behaves like entropy production in regions where trajectories intersect, and so vorticity can be generated in the mean (fluid) velocity field. Vorticity also arises from isocurvature initial conditions. Equation (2.21) implies _S ²S for long wavelengths in the linear regime, giving a baroclinic torque proportional to _S × S (²S) × S, which is nonzero in general (though it appears only in second-order perturbation theory).

For most structure formation models, vorticity generation is quite small until shocks form (or trajectories intersect, for collisionless dark matter). In this case, one may obtain the velocity potential from the line integral of the velocity field:

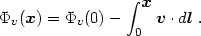(2.26)

Taking the path to be radial with the observer in the middle allows one to reconstruct the velocity potential, and therefore the transverse velocity components, from the radial component. This idea underlies the potential flow reconstruction method, POTENT (Bertschinger & Dekel 1989). If the (smoothed) density fluctuations are sufficiently small for linear theory to be valid, we can estimate the density fluctuation field from an additional divergence. If pressure is unimportant, so k << k_J and ₊(), the linearized continuity equation gives

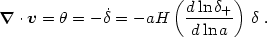(2.27)

For a wide range of cosmological models, d ln₊ / d ln a f () ^0.6 depends primarily on the mass density parameter and weakly on other cosmological parameters (Peebles 1980, Lahav et al. 1991). Thus, combining measurements of v (radial components from galaxy redshifts and distances) and independent measurements of (from the galaxy density field plus an assumption about how dark matter is distributed relative to galaxies) allows estimation of (Dekel et al. 1993). A review of the POTENT techniques and results is given by Dekel (1994).