3.4. Nonrelativistic evolution including self-gravity

Now that we have developed the basic techniques for solving the linearized nonrelativistic Vlasov equation, adding self-gravity of the collisionless particles is easy. We simply add a contribution to arising from . In eq. (3.17), if we have a mixture of hot and cold dark matter, (_c + ); additional contributions may be added as appropriate. Equation (3.22) becomes

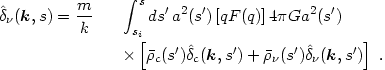(3.33)

This equation was first derived (in a slightly different form) by Gilbert (1966) and is known as the Gilbert equation. Note that in the self-gravitating case appears both inside and outside an integral. Equation (3.33) is a Volterra integral equation of the second kind. Bertschinger & Watts (1988) present a numerical quadrature solution method.

Using the same trick as in the previous subsection, we can convert the Gilbert equation to a differential equation for , if the unperturbed phase space density distribution is approximated by the form f(p) of eq. (3.26). The result is

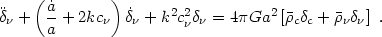(3.34)

With a suitable choice for the parameter , the solution of eq. (3.34) provides a good match (to within a few percent, in general) to the solution of the Gilbert equation using the correct Fermi-Dirac distribution for massive neutrinos (Setayeshgar 1990). Therefore, it may be used for obtaining quick estimates of the density perturbations of nonrelativistic hot dark matter.