3.3. Nonrelativistic evolution in an external gravitational field

In this section we consider hot dark matter made of nonrelativistic massive neutrinos with << so that their self-gravity is unimportant. The gravitational potential (x, ) (using comoving coordinates) is assumed to be given from other sources such as cold dark matter in a mixed hot and cold dark matter model.

We can solve the Vlasov equation (3.9) approximately by replacing f / p with the unperturbed term f₀ / p. This approximation is valid for |f - f₀| << f₀, and should suffice to demonstrate the collisionless damping of small-amplitude fluctuations.

A quadrature solution of the Vlasov equation can be obtained provided that we change the time variable from to s = d / a = dt / a² and then Fourier transform the spatial variable:

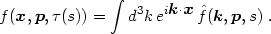(3.16)

The gravitational potential is transformed similarly. Integrating eq. (3.9) over s, we obtain the solution

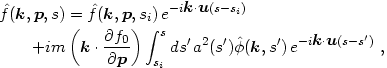(3.17)

where u = p / m and s_i is an initial time. If the initial phase space distribution is unperturbed, then (k, p, s_i) = f₀(p) (k). Note that the complex exponentials in eq. (3.17) correspond to the propagation of the phase space density along the characteristics dx / ds = u. This motion is called free-streaming.

To understand the behavior of the free-streaming solution, let us examine the integral term of eq. (3.17), which is proportional to

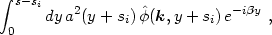(3.18)

where k ^. p / m and y = s' - s_i. For sufficiently slowly moving neutrinos, is small enough so that y << 1. This condition corresponds to a free-streaming distance along k that is much less than k^-1. These neutrinos do not move far from the crests and troughs of the plane wave perturbation. Neglecting the exponential, the time dependence of the solution is the same as for cold dark matter.

If, however, y >> 1, corresponding to neutrinos traveling across many wavelengths of a perturbation, the rapid oscillations of the exponential lead to cancellation in the integrand of eq. (3.18) and suppression of the neutrino phase space density perturbation. This effect, known as free-streaming damping, occurs because neutrinos that are initially at the crests or troughs of density waves move so far that they distribute themselves almost uniformly. The small gravitational acceleration induced by the external potential is inadequate to collect the fast-moving neutrinos in dense regions.

Thus, perturbations can grow only for the neutrinos that move less than about one wavelength per Hubble time. Our analysis confirms the rough picture we sketched in the beginning of this lecture.

We can obtain the net density perturbation (in Fourier space) by integrating eq. (3.17) over momenta:

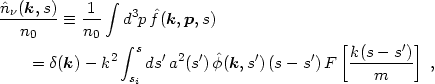(3.19)

where n₀ = d³p f₀(p) is the mean comoving number density and F is the Fourier transform - with respect to the momentum! - of the unperturbed distribution function:

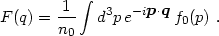(3.20)

For the relativistic Fermi-Dirac distribution appropriate to hot dark matter, F has the series representation (Bertschinger & Watts 1988)

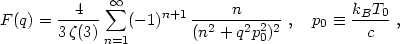(3.21)

where (3) = 1.202... is the Riemann zeta function and F(0) = 1.

Equation (3.19) does not give much insight into free-streaming damping. To get a better feel for the physics, as well as a simpler approximation for treating hot dark matter, we now show how to convert eq. (3.19) into a differential equation for the evolution of the hot dark matter density perturbation similar to eq. (2.12) for a perfect collisional fluid. This may seem impossible a priori - how can the dispersive behavior of a collisionless gas be represented by fluid-like differential equations? - but we shall see that it is possible if we approximate f₀(p) by a form differing slightly from the Fermi-Dirac distribution. The results, although not exact, will give us additional insight into the behavior of collisionless damping.

The first step is to rewrite eq. (3.19) for the Fourier transform of the density fluctuation :

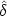
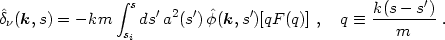(3.22)

Next, we differentiate twice with respect to the time coordinate s:

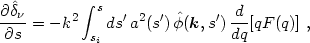(3.23)

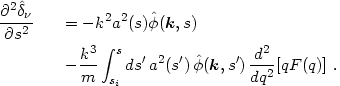(3.24)

Note the appearance of a non-integrated source term in the second derivative, arising because d (qF) / dq does not vanish at s = s' (q = 0) while qF does.

Next, we note that if d²(qF) / dq² were to equal a linear combination of d (qF) / dq and (qf ), then we could write the integral in equation (3.24) as a linear combination of / s and . Unfortunately, this is not the case for F(q) given by eq. (3.21). However, it is true for the family of distribution functions whose Fourier transforms are

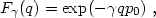(3.25)

for any dimensionless constant . This defines the family of phase space density distributions

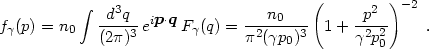(3.26)

For this form of unperturbed distribution we have

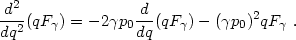(3.27)

Combining eqs. (3.22)-(3.24) and (3.27), we get

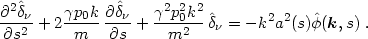(3.28)

To put this result into a form similar to the acoustic wave equation we derived for a collisional fluid, we define the characteristic proper thermal speed

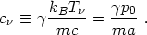(3.29)

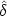
Next, we change the time variable from s back to with d / ds = a. Finally, we assume that the source term gravitational potential is given by the Poisson equation for a perturbation _c in a component with mean mass density _c (e.g., cold dark matter - recall that we are neglecting the self-gravity of the neutrinos). Dropping the hat on , the result is

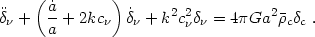(3.30)

This equation was first derived by Setayeshgar (1990). It is approximate (not exact) for the linear evolution of massive neutrinos because we replaced the Fermi-Dirac distribution by eq. (3.26). It is not difficult to show that eq. (3.26) is the only form of the distribution function for which eq. (3.17) can be reduced to a differential equation for (k, ). (Even the Maxwell-Boltzmann distribution fails - a collisionless gas with this distribution initially does not evolve the same way as a collisional gas with the Maxwell-Boltzmann distribution function for all times.) One should also bear in mind that does not contain all the information needed to characterize perturbations in a collisionless gas (Ma & Bertschinger 1994a). Complete information resides in (k, p, s).

Even if eq. (3.30) is not exact for massive neutrinos and does not fully specify the perturbations, it provides an extremely helpful pedagogic guide to the physics of collisionless damping. We see at once that a gravitational source can induce density perturbations in a collisionless component, but the source competes agains acoustic (k² c²) and damping ( / a + 2kc) terms. Roughly speaking, hot dark matter behaves like a collisional gas with an extra free-streaming damping term.

Does the k² c² term imply that a collisionless gas can support acoustic oscillations? To check this we consider the limit kc >> 1 so that the Hubble damping and gravitational source terms are negligible. We then have

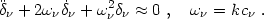(3.31)

Because changes very slowly with time compared with the oscillation timescale ^-1, eq. (3.31) is a linear differential equation with constant coefficients and is easily solved to give the two modes

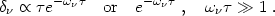(3.32)

Neither solution oscillates! The first one begins to grow but is rapidly damped on a timescale , after the typical neutrino has had time to cross one wavelength.

Because the damping time (kc)^-1 is proportional to the wavelength, short-wavelength perturbations are damped most strongly. At any given time , perturbations of comoving wavelength less than about c are attenuated. This is precisely the free-streaming distance we introduced in the beginning of this lecture, equation (3.2).

Our results enable us to understand why the hot dark matter transfer function is similar to that of cold dark matter for long wavelengths but cuts off sharply for short wavelengths (Bond & Szalay 1983). During the radiation-dominated era, a() . While the massive neutrinos were relativistic, c c was constant. The comoving free-streaming distance increased, c a, with hot dark matter perturbations being erased on scales up to the Hubble distance. After the neutrinos became nonrelativistic, however, c is given by eq. (3.29), c a^-1. Thus, the free-streaming distance saturates at the Hubble distance when the neutrinos become nonrelativistic. During the matter-dominated era, a() ₂ (while 1) so that the free-streaming distance decreases: c a^-1/2. However, free-streaming has already erased the hot dark matter perturbations on scales up to the maximum free-streaming distance, eq. (3.3). Only if the perturbations are re-seeded, e.g. by cold dark matter or topological defects, will small-scale power be restored to the hot dark matter.