4.1.2. Summary of essential relativity

We adopt the following conventions and notations, similar to those of Misner, Thorne & Wheeler (1973). Units are chosen so that c = 1. The metric signature is (- , + , + , +). The unperturbed background spacetime is Robertson-Walker with scale factor a() expressed in terms of conformal time. A dot (or ) indicates a conformal time derivative. The comoving expansion rate is written () / a = aH. The scale factor obeys the Friedmann equation,

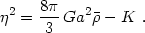(4.1)

The Robertson-Walker line element is written in the general form using conformal time and comoving coordinates xⁱ:

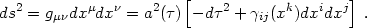(4.2)

Latin indices (i, j, k, etc.) indicate spatial components while Greek indices (µ, , , etc.) indicate all four spacetime components; we assume a coordinate basis for tensors. Summation is implied by repeated upper and lower indices. The inverse 4-metric g^µ (such that g^µ g = ^µ) is used to raise spacetime indices while the inverse 3-metric ^ij (^ij _jk = _kⁱ) is used to raise indices of 3-vectors and tensors. Three-tensors are defined in the spatial hypersurfaces of constant with metric _ij and they shall be clearly distinguished from the spatial components of 4-tensors. We shall see as we go along how this "3+1 splitting" of spacetime works when there are metric perturbations.

Many different spatial coordinate systems may be used to cover a uniform-curvature 3-space. For example, there exist quasi-Cartesian coordinates (x, y, z) in terms of which the 3-metric components are

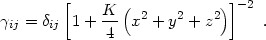(4.3)

We shall use 3-tensor notation to avoid restricting ourselves to any particular spatial coordinate system. Three-scalars, vectors, and tensors are invariant under transformations of the spatial coordinate system in the background spacetime (e.g., rotations). A 3-vector may be written A = Aⁱe_i where e_i is a basis 3-vector obeying the dot product rule e_i ^. e_j = _ij. A second-rank 3-tensor may be written (using dyadic notation and the tensor product) h = h^ije_i e_j. We write the spatial gradient 3-vector operator = eⁱ _i (_i / xⁱ) where e^{i .} e_j = _jⁱ. The experts will recognize eⁱ as a basis one-form but we can treat it as a 3-vector eⁱ = ^ij e_j because of the isomorphism between vectors and one-forms. Because the basis 3-vectors in general have nonvanishing gradients, we define the covariant derivative (3-gradient) operator _i with _{i jk} = 0. If the space is flat (K = 0) and we use Cartesian coordinates, then _ij = _ij, _i = _i, and the 3-tensor index notation reduces to elementary Cartesian notation. If K 0, the 3-tensor equations will continue to look like those in flat space (that is why we use a 3+1 splitting of spacetime!) except that occasionally terms proportional to K will appear in our equations.

Our application is not restricted to a flat Robertson-Walker background but allows for nonzero spatial curvature. This complicates matters for two reasons. First, we cannot assume Cartesian coordinates. As a result, for example, the Laplacian of a scalar and the divergence and curl of a 3-vector involve the determinant of the spatial metric, det{_ij}:

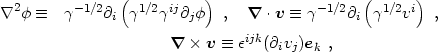(4.4)

where ^ijk = ^-1/2 [ijk] is the three-dimensional Levi-Civita tensor, with [ijk] = + 1 if {ijk} is an even permutation of {123}, [ijk] = - 1 for an odd permutation, and 0 if any two indices are equal. The factor ^-1/2 ensures that ^ijk transforms like a tensor; as an exercise one can show that _ijk = ^1/2 [ijk].

The second complication for K 0 is that gradients do not commute when applied to 3-vectors and 3-tensors (though they do commute for 3-scalars). The basic results are

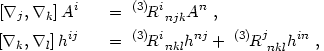(4.5)

where [_j, _k] (_{j k} - _{k j}). The commutator involves the spatial Riemann tensor, which for a uniform-curvature space with 3-metric _ij is simply

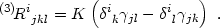(4.6)

Finally, we shall need the evolution equations for the full spacetime metric g_µ. These are given by the Einstein equations,

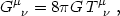(4.7)

where T^µ is the stress-energy tensor and G^µ is the Einstein tensor, related to the spacetime Ricci tensor R_µ by

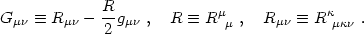(4.8)

The spacetime Riemann tensor is defined according to the convention

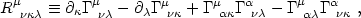(4.9)

where the affine connection coefficients are

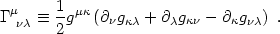(4.10)

We see that the Einstein tensor involves second derivatives of the metric tensor components, so that eq. (4.7) provides second-order partial differential equations for g_µ.

The reader who is not completely comfortable with the material summarized above may wish to consult an introductory general relativity textbook, e.g. Schutz (1985).