4.2. Classification of metric perturbations

Now we consider small perturbations of the spacetime metric away from the Robertson-Walker form:

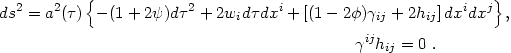(4.11)

We have introduced two 3-scalar fields (x, ) and (x, ), one 3-vector field w(x, ) = w_i eⁱ, and one symmetric, traceless second-rank 3-tensor field h(x, ) = h_ij eⁱ e^j. No generality is lost by making h_ij traceless since any trace part can be put into . The factors of 2 and signs have been chosen to simplify later expressions.

Equation (4.11) is completely general: g_µ has 10 independent components and we have introduced 10 independent fields (1 + 1 + 3 + 5 for + + w + h). In fact, only 6 of these fields can represent physical degrees of freedom because we are free to transform our 4 coordinates (, xⁱ) without changing any physical quantities. Infinitesimal coordinate transformations, called gauge transformations, result in changes of the fields (, , w, h) because the spacetime scalar ds² = g_µ dx^µ dx must be invariant under general coordinate transformations. We shall explore the consequences of this invariance later. Coordinate invariance complicates general relativity compared with other gauge theories (e.g., electromagnetism) in which the spacetime coordinates are fixed while other variables change under the appropriate gauge transformations.

Unless stated explicitly to the contrary, in the following we shall treat the perturbation variables (, , w_i, h_ij) exclusively as 3-tensors (of rank 0, 1, or 2 according to the number of indices) with components raised and lowered using ^ij and _ij. In doing this we choose to use _ij as the 3-metric in the perturbed hypersurface of constant despite the fact that the spatial part of the 4-metric (divided by a²) is given by (1 - 2)_ij + 2h_ij. This treatment is satisfactory because we will assume that the metric perturbations are small and we will neglect all terms quadratic in them. However, we will use g^µ to raise 4-vector components: G^µ = g^µ G. Do take care to distinguish Latin from Greek!

We have introduced 3-scalar, 3-vector, and 3-tensor perturbations. (From now on we will drop the prefix 3- since it should be clear from the context whether 3- or 4- is implied.) Are these the famous scalar, vector, and tensor metric perturbations? Not quite! Recall the decomposition of a vector into longitudinal and transverse parts:

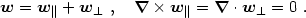(4.12)

Since w_|| = -w for some scalar w, how can it be called a vector perturbation? By definition, only the transverse component w represents a vector perturbation.

There is a similar decomposition theorem for tensor fields: Any differentiable traceless symmetric 3-tensor field h_ij(x) may be decomposed into a sum of parts, called longitudinal, solenoidal, and transverse:

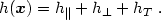(4.13)

The various parts are defined in terms of a scalar field h(x) and transverse (or solenoidal) vector field h(x) such that

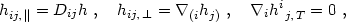(4.14)

where we have denoted symmetrization with parentheses and have employed the traceless symmetric double gradient operator:

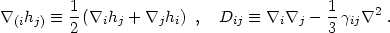(4.15)

Note that the divergences of h_|| and h are longitudinal and transverse vectors, respectively (it doesn't matter which index is contracted on the divergence since h is symmetric):

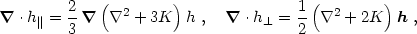(4.16)

where ² h (² hⁱ) e_i. (We do not call h the transverse part, as we would by extension from w, because "transverse" is conventionally used to refer to the tensor part.) The longitudinal tensor h_|| is also called the scalar part of h, the solenoidal part h is also called the vector part, and the transverse-traceless part h_T is also called the tensor part. This classification of the spatial metric perturbations h_ij was first performed by Lifshitz (1946).

The purpose of this decomposition is to separate h_ij into parts that can be obtained from scalars, vectors, and tensors. Is the decomposition unique? Not quite. It is clear, first of all, that h and h_i are defined only up to a constant. But there may be additional freedom (Stewart 1990).

First, the vector h is defined only up to solutions of Killing's equation _i h_j + _j h_i = 0, called Killing vectors (Misner et al. 1973). The reader can easily verify that one such solution (using the quasi-Cartesian coordinates of eq. 4.3) is (h_x, h_y, h_z) = (y, - x, 0). In an open space (K 0) this solution would be excluded because it is unbounded -- our perturbations should not diverge! - but in a closed space (K > 0) the coordinates have a bounded range. This Killing vector, and its obvious cousins, correspond to global rotations of the spatial coordinates and not to physical perturbations.

Next, there may also be non-uniqueness associated with the tensor (and scalar) component:

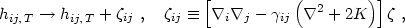(4.17)

where is some scalar field. From eqs. (4.5) and (4.6) one can show ²(_i ) = _i(² + 2K) so that _{i j}ⁱ = 0 as required for the tensor component. However, we also require h_{ij, T} to be traceless, implying (² + 3K) = 0. Thus, the tensor mode is defined only up to eq. (4.17) with bounded solutions of (² + 3K) = 0. In fact, this condition also implies _ij = D_ij , so we may equally well attribute _ij to the scalar mode h_{ij, ||} . Thus, we are free to add any multiple of to h (the scalar mode) provided we subtract D_ij from the tensor mode. In an open space (K 0) there are no nontrivial bounded solutions to (² + 3K) = 0 but in a closed space (K > 0) there are four linearly independent solutions (Stewart 1990). Once again, these solutions correspond to redefinitions of the coordinates with no physical significance. Kodama & Sasaki (1984, Appendix B) gave a proof of the tensor decomposition theorem, but they missed the additional vector and scalar/tensor mode solutions present in a closed space. In practice, it is easy to exclude these modes, and so we shall ignore them hereafter.

Thus, we conclude that the most general perturbations of the Robertson-Walker metric may be decomposed at each point in space into four scalar parts each having 1 degree of freedom (, , w_||, h_||), two vector parts each having 2 degrees of freedom (w, h), and one tensor part having 2 degrees of freedom (h_T, which lost 3 degrees of freedom to the transversality condition). The total number of degrees of freedom is 10.

Why do we bother with this mathematical classification? First and foremost, the different metric components represent distinct physical phenomena. (By way of comparison, in previous lectures we have already seen that v_|| and v play very different roles in fluid motion.) Ordinary Newtonian gravity obviously is a scalar phenomenon (the Newtonian potential is a 3-scalar), while gravitomagnetism and gravitational radiation - both of which are absent from Newton's laws, and will be discussed below - are vector and tensor phenomena, respectively. Moreover, this spatial decomposition can also be applied to the Einstein and stress-energy tensors, allowing us to see clearly (at least in some coordinate systems) the physical sources for each type of gravity. Finally, the classification will help us to eliminate unphysical gauge degrees of freedom. There are at least four of them, corresponding to two of the scalar fields and one transverse vector field.

We will not write the weak-field Einstein equations for the general metric of eq. (4.11). Instead, we will consider only two particular gauge choices, each of which allows for all physical degrees of freedom (and more, in the case of synchronous gauge). First, however, we must examine the stress-energy tensor.