4.4. Synchronous gauge

Synchronous gauge, introduced by Lifshitz (1946) in his pioneering calculations of cosmological perturbation theory, is defined by the conditions = w_i = 0, which eliminate two scalar fields ( and the longitudinal part of w) and one transverse vector field (w). It is not difficult to show that synchronous coordinates can be found for any weakly-perturbed spacetime. However, the synchronous gauge conditions do not eliminate all gauge freedom. This has in the past led to considerable confusion (for discussion see Press & Vishniac 1980 and Bardeen 1980).

Synchronous gauge has the property that there exists a set of comoving observers who fall freely without changing their spatial coordinates. (This is nontrivial when one notes that in order to remain at a fixed terrestrial latitude, longitude, and altitude above the surface of the earth it is necessary to accelerate everywhere except in geosynchronous orbits.) These observers are called "fundamental" comoving observers. The existence of fundamental observers follows from the geodesic equation

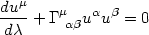(4.26)

for the trajectory x^µ(), where d = (- ds²)^1/2 for a timelike geodesic and u^µ = dx^µ / d. With = w_i = 0, eq. (4.10) gives ₀₀ⁱ = 0, implying that uⁱ = 0 is a geodesic.

Each fundamental observer carries a clock reading conformal time = dt / a(t) and a fixed spatial coordinate label xⁱ. The clocks and labels of the fundamental observers are taken to define the coordinate values at all spacetime points (assuming that these hypothetical observers densely fill space). The residual gauge freedom in synchronous gauge arises from the freedom to adjust the initial settings of the clocks and the initial coordinate labels of the fundamental observers.

Because the spatial coordinates xⁱ of each fundamental observer are held fixed with time, the xⁱ in synchronous gauge are Lagrangian coordinates. This implies that the coordinate lines become highly deformed when the density perturbations become large. When the trajectories of two fundamental observers intersect the coordinates become singular: two different sets of x^µ label the same spacetime event. This flaw of synchronous gauge is not apparent if | / | << 1 and the initial coordinate labels are nearly unperturbed, so this gauge may be used successfully (with some care required to avoid contamination of physical variables by the residual gauge freedom) in linear perturbation theory.

To be consistent with the conventional notation used for synchronous gauge (Lifshitz 1946; Lifshitz & Khalatnikov 1963; Weinberg 1972; Peebles 1993), in this section only we shall absorb into h_ij and double h_ij:

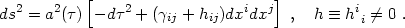(4.27)

Using this line element and the definitions of the Ricci and Einstein tensors, it is straightforward (if rather tedious) to derive the components of the perturbed Einstein tensor:

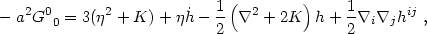(4.28)

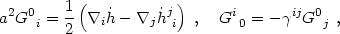(4.29)

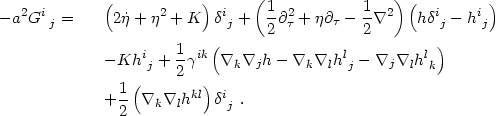(4.30)

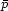
One can easily verify that the unperturbed parts of the Einstein equations G⁰₀ = 8 GT⁰₀ = -8 G and Gⁱ_j = 8 GTⁱ_j = 8G _jⁱ give the Friedmann and energy-conservation equations for the background Robertson-Walker spacetime.

Our next goal is to separate the perturbed Einstein equations into scalar, vector, and tensor parts. First we must decompose the metric perturbation field h_ij as in eqs. (4.13)-(4.15), with a term added (and the notation changed slightly) to account for the trace of h_ij:

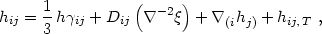(4.31)

where D_ij was defined in eq. (4.15). We require _i hⁱ = _i hⁱ_T = 0 to ensure that the last two parts of h_ij are purely solenoidal (vector mode) and transverse-traceless (tensor mode) contributions. The scalar mode variables are h and ^-2 , whose Laplacian is . We shall not worry about how to invert the Laplacian on a curved space but simply assume that it can be done if necessary.

The perturbed Einstein equations now separate into 7 different parts according to the spatial symmetry:

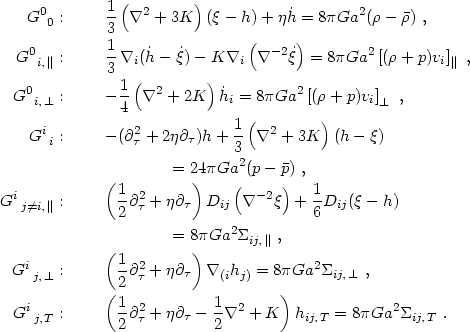(4.32) (4.33) (4.34) (4.35) (4.36) (4.37) (4.38)

The derivation of these equations is straightforward but tedious. They have decomposed naturally into separate equations for the scalar, vector, and tensor parts of the metric perturbation, with the sources for each given by the appropriate part of the energy-momentum tensor. However, there are more equations than unknowns! There are four scalar equations for and h, two vector equations for h_i, and one tensor equation for h_ij,T. How can this be?

Before answering this question, let us note another interesting feature of the equations above, which will provide a clue. The equations arising from G⁰_µ involve only a single time derivative of the scalar and vector mode variables, while those arising from Gⁱ_µ have two time derivatives, as we might have expected for equations of motion for the gravitational fields. This means that we could discard eqs. (4.32)-(4.34) and be left with exactly as many second-order in time equations as unknown fields. Alternatively, we could discard eqs. (4.35)-(4.37) and be left with exactly enough first-order in time equations for the scalar and vector modes. Only the tensor mode evolution is uniquely specified by a second-order wave equation.

The reason for this redundancy is that the twice-contracted Bianchi identities of differential geometry, _µ G^µ = 0, force the Einstein eqs. (4.7) to imply _µ T^µ = 0. The Einstein equations themselves contain redundancy, as we can check explicitly here. By combining the time derivative of eq. (4.32) and the divergence of eqs. (4.33) and (4.34) one obtains the perturbed part of eq. (4.24) (note, however, that - h/6). Similarly, eq. (4.25) follows from the time derivative of eqs. (4.33) and (4.34) combined with the gradient of eqs. (4.35)-(4.37). Because we require the equations of motion for the matter and radiation to locally conserve the net energy-momentum, three of the perturbed Einstein eqs. (4.32)-(4.38) are redundant.

In the literature, G⁰₀ = 8 GT⁰₀ is often called the "ADM energy constraint" and G⁰_i = 8 GT⁰_i is called the "ADM momentum constraint" equation. The 3+1 space-time decomposition of the Einstein equations into constraint and evolution equations was developed in detail by Arnowitt, Deser & Misner (1962, ADM) and applied to cosmology by Durrer & Straumann (1988) and Bardeen (1989). The ADM constraint equations may be regarded as providing initial-value constraints on (h, , , 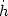, 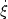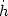_i) and the matter variables. If these constraints are satisfied initially (this is required for a consistent metric), and if eqs. (4.35)-(4.37) are used to evolve (h, , , 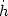, 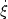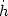_i) while the matter variables are evolved so as to locally conserve the net energy-momentum, then the ADM constraints will be fulfilled at all later times. (This follows from the results stated in the preceding paragraph.) In effect, the Einstein equations have built into themselves the requirement of energy-momentum conservation for the matter. If one were to integrate eqs. (4.35)-(4.37) correctly but to violate energy-momentum conservation, then eqs. (4.32)-(4.34) would be violated.

In practice, we may find it preferable to regard the ADM constraints alone - and not eqs. (4.35)-(4.37) - as giving the actual field equations for the scalar and vector metric perturbations. They have fewer time derivatives and hence are easier to integrate. Equations (4.35)-(4.37) are not necessary at all (although they may be useful for numerical checks) because they can always be obtained by differentiating eqs. (4.32)-(4.34) and using energy-momentum conservation.

This situation becomes clearer if we compare it with Newtonian gravity. The field equation ² = 4 Ga² is analogous to eq. (4.32). (We shall see this equivalence much more clearly in the Poisson gauge below.) Let us take the time derivative: ² = 4 G(a² ). If we now replace ( ) using the continuity equation, we obtain a time evolution equation for ² analogous to the divergence of eq. (4.33). The solutions to this evolution equation obey the Poisson equation if and only if the initial obeys the Poisson equation. Why should one bother to integrate ² in time when the solution can always be obtained instantaneously from the Poisson equation? Viewed in this way, we would say that the extra time derivatives in the Gⁱ_µ equations have nothing to do with gravity per se. The real field equations for the scalar and vector modes come from the ADM constraint equations.

If the scalar and vector metric perturbations evolve according to first-order in time equations, their solutions are not manifestly causal (e.g., retarded solutions of the wave equation). We shall discuss this point in detail in section 4.7. However, for now we may note that the tensor mode obeys the wave eq. (4.38). The solutions are the well-known gravity waves which, as we shall see, play a key role in enforcing causality. The source for these waves is given by the transverse-traceless stress (generated, for example, by two masses orbiting around each other). The term arises because we use comoving coordinates and the K term arises as a correction to the Laplacian in a curved space; otherwise the vacuum solutions are clearly waves propagating at the speed of light. Abbott & Harari (1986) show that eq. (4.38) is the Klein-Gordon equation for a massless spin-two particle.