4.8. Hamiltonian dynamics of particles

In this section we extend to general relativity the Hamiltonian formulation of particle dynamics that is familiar in Newtonian mechanics. In the process we shall obtain further insight into the physical meaning of the gravitational fields discussed in the previous section. A preliminary version of this material appears in (Bertschinger 1993). A related presentation in the context of gravitational fields near black holes is given by Thorne et al. (1986).

As in the nonrelativistic case, we choose a Hamiltonian that is related to the energy of a particle. Consequently, our approach is not manifestly covariant; the energy depends on how spacetime is sliced into hypersurfaces of constant conformal time because the energy is the time component of a 4-vector. Nevertheless, our approach is fully compatible with general relativity; we must only select a specific gauge. For simplicity we shall adopt the Poisson gauge, eq. (4.11) with gauge conditions eq. (4.46). We assume that the metric perturbations are given by a solution of the field eqs. (4.49)-(4.55). Our Hamiltonian will include only the degrees of freedom associated with one particle; one can generalize this to include many particles (even treated as a continuum) and the metric variables (Arnowitt et al. 1962; Misner et al. 1973; Salopek & Stewart 1992) but this involves more machinery than necessary for our purposes.

The goal of the Hamiltonian approach is to obtain equations of motion for trajectories in the single-particle phase space consisting of the spatial coordinates xⁱ and their conjugate momenta. The first question is, what are the appropriate conjugate momenta? This question practically answers itself when we express the action scalar in terms of our coordinates:

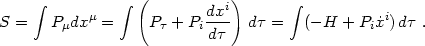(4.63)

Note that we have automatically expressed the action in terms of the covariant (lower-index) components of the 4-momentum (also known as the components of the momentum one-form). We can read off the Hamiltonian and conjugate momenta using the fact that S = Ld where L(xⁱ, 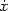_j, ) is the Lagrangian, which is related to the Hamiltonian H(xⁱ, P_j, ) by the Legendre transformation L = P_{i 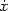i} - H. The Hamiltonian therefore is H = - P - despite appearances, we shall see that this is not in general the proper energy - and the conjugate momenta equal the covariant spatial components of the 4-momentum. Indeed, we may simply define the conjugate momenta and Hamiltonian in this way. (Care should be taken not to confuse the Hamiltonian H with the Hubble parameter H and the gravitomagnetic field H!)

With these definitions, H and P_i correspond to the usual quantities encountered in elementary nonrelativistic mechanics, but we need not rely on this fact. For any choice of spacetime geometry and coordinates we may determine the corresponding Hamiltonian and conjugate momenta from the 4-momentum components: for a particle of mass m, H = - mg_0µdx^µ / d, P_i = mg_iµ dx^µ / d where d measures proper time along the particle trajectory. As an exercise, one may show that with cylindrical coordinates (r, , z) for a nonrelativistic particle of mass m in Minkowski spacetime, P_r = m is the radial momentum, P = mr² 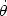is the angular momentum about e_z, P_z = m 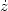is the linear momentum along e_z, and H = E m + (P_r² + P² / r² + P_z²) / 2m is the proper energy (including the rest mass energy). We shall determine the functional form H(xⁱ, P_j, ) for our perturbed Robertson-Walker spacetime below.

First, however, let us show that our approach leads to the usual canonical Hamilton's equations of motion, rigorously justifying our choices H = - P and P_i being the momentum conjugate to xⁱ. To do this we simply vary the phase space trajectory {xⁱ(), P_j()} to {xⁱ + xⁱ, P_j + P_j}, treating xⁱ() and P_j() as independent variations and computing the variation of the action of eq. (4.63):

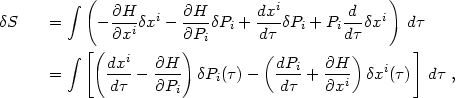(4.64)

where we have assumed P_i xⁱ = 0 at the endpoints of integration. Requiring the action to be stationary under all variations, S = 0, we obtain the standard form of Hamilton's equations:

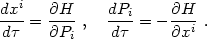(4.65)

Thus, Hamilton's equations give phase space trajectories in general relativity just as they do in nonrelativistic mechanics.

Our next step is to determine the Hamiltonian for the problem at hand. We shall assume that the particle falls freely in the perturbed Robertson-Walker spacetime described in the Poisson gauge. For comparison with the nonrelativistic results, it is useful to relate the 4-momentum components to the proper energy and 3-momentum measured by a comoving observer (i.e., one at fixed xⁱ), E and p_i:

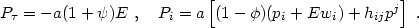(4.66)

The first equation follows from E = - u^µP_µ where u^µ is the 4-velocity of a comoving observer from eq. (4.21) with v = 0, while the second equation follows from projecting P_µ into the hypersurface normal to u^µ and normalizing to give the proper 3-momentum. The weak-field approximation has been made (i.e., terms quadratic in the metric perturbations are neglected), but the particle motion is allowed to be relativistic. The factors a(1 + ) and a(1 - ) are obviously needed from eq. (4.11) to convert proper quantities into coordinate momenta, the Ew_i term arises because our space and time coordinates are not orthogonal if there is a vector mode, and the h_ijp^j term arises because our spatial coordinates are not orthogonal if there is a tensor mode. The reader may verify that the 4-momentum satisfies the normalization condition g^µ P_µ P = - E² + p² = - m², and that this condition would be violated in general without the vector and tensor terms in P_i.

Using these results it is easy to show that, to first order in the metric perturbations, the Hamiltonian is

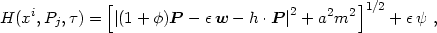(4.67)

where

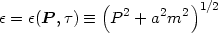(4.68)

and the squares and dot products of 3-vectors such as p_i, P_i, and h^ijP_j are computed using the 3-metric, e.g., P² = ^ij P_iP_j. Using the Hamiltonian of eq. (4.67), eqs. (4.65) may be shown to be fully equivalent to the geodesic equations for a freely falling particle moving in the metric of eq. (4.11), and they could also be obtained starting from a Lagrangian approach. The advantage of the Hamiltonian approach is that it treats positions and conjugate momenta equally as is needed for a phase space description.

Equation (4.67) appears strange at first glance. To understand it better, let us recall the standard form for the Hamiltonian of a particle with charge e in electromagnetic fields (with being the electrostatic potential):

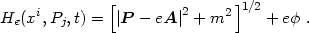(4.69)

Note that the proper momentum is p = P - eA where P is the conjugate momentum. Comparing eqs. (4.67) and (4.69), we see that they are very similar aside from the tensor term h ^. P present in the gravitational case. The few remaining differences are easily understood. To compensate for spatial curvature - effectively a local change of the units of length - in the gravitational case P is multiplied by (1 + ). The electric charge e is replaced by the gravitational charge (energy!); to zeroth order in the perturbations = H = aE. The use of comoving coordinates is responsible for the factors of a(). The gravitational (gravitomagnetic) vector potential is w - as we anticipated in eq. (4.61). Finally, the electrostatic potential energy e is replaced in the gravitational case by . The strong analogy between the vector mode and magnetism accounts for the adjective "gravitomagnetic."

A different interpretation of the gravitomagnetic contribution to the Hamiltonian will clarify the relation of gravitomagnetism and the dragging of inertial frames. In section 4.3 we noted that w is the velocity of the comoving frame relative to a locally inertial frame (the normal frame). For w² << 1, p' p + Ew is therefore the proper momentum in the normal frame. According to eq. (4.66), then, neglecting the scalar and tensor modes, P is the comoving momentum (i.e., multiplied by a) in the normal frame, P = ap', while P - w (the combination present in the Hamiltonian) is the comoving momentum in the comoving frame. It is logical that the Hamiltonian should depend on the latter quantity; after all, we are using non-orthogonal comoving spacetime coordinates. However, it is equally reasonable that the conjugate momentum should be measured in the frame normal to the hypersurface = constant. Thus, it is simply the offset between these two frames - if one likes, the dragging of inertial frames - that is responsible for the - w term in eq. (4.67). Gravitomagnetism - and similarly magnetism, if one interprets (e/m)A as a velocity - can be viewed as a kinematical effect!

The tensor mode, corresponding to gravitational radiation, gives an extra term in the Hamiltonian - really in the relation between the proper and conjugate momenta - that is not present in the case of electromagnetism. Geometrically, h corresponds simply to a local volume-preserving deformation of the spatial coordinate lines, and in this way it simply extends the effect of the spatial curvature term P in eq. (4.67) ( represents an orientation-preserving dilatation of the coordinate lines). However, what is more important is the dynamical effect of these terms, neither of which is familiar in either Newtonian gravity or electromagnetism.

To study the dynamics of particle motion we use Hamilton's eqs. (4.65) with the Hamiltonian of eq. (4.67). In terms of the proper momentum p measured by a comoving observer, Hamilton's equations in the Poisson gauge become

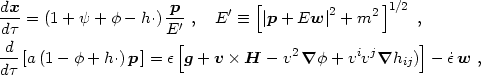(4.70)

where we have defined E' to be the proper energy in the normal frame, v is the peculiar velocity (in the weak-field limit it doesn't matter whether it is the coordinate or proper peculiar velocity nor whether it is measured in the comoving or normal frame) and g and H are the gravitoelectric and gravitomagnetic fields given by eqs. (4.61). The dot following h indicates the three-dimensional dot product, with h ^. p being a 3-vector.

Equations (4.70) appear rather complicated at first but each term can be understood without much difficulty. First, note that the factor (1 + + - h ^. ) in the first equation is present solely to convert from a proper velocity to a coordinate velocity dx / d according to the metric eq. (4.11). Using the transformation from the normal (primed) to comoving frame, p = p' - Ew p' - E'w, the equation for dx / d implies that the proper velocity in the comoving frame must equal p/E' = p' / E' - w. This is identically true because p' / E' is the proper velocity in the normal frame, whose velocity relative to the comoving frame is - w.

Similarly, the factor a(1 - + h ^.) in the momentum equation simply converts the proper momentum p to the comoving momentum in the comoving frame, P - w (cf. eq. 4.66). The first two terms on the right-hand side have exactly the same form as the Lorentz force law of electrodynamics, with the electric charge e replaced by the comoving energy and the electric and magnetic fields E and B replaced by their gravitational counterparts g and H. Thus, general relativity in the weak-field limit gives "forces" on freely-falling bodies (when expressed in the Poisson gauge) that are very similar to those of electromagnetism!

The remaining terms in the momentum equation have no counterpart in electrodynamics or Newtonian gravity. There are two gravitational force terms quadratic in the velocity arising from spatial curvature. The first one is present for a scalar mode and is responsible for the fact that photons are deflected twice as much as nonrelativistic particles in a gravitostatic field ( = in the Newtonian limit). The second term represents, in effect, scattering of moving particles by gravitational radiation. A gravity wave traveling in the z-direction will accelerate a particle in this direction if the particle has nonzero velocity in the x-y plane (the direction of polarization of the transverse gravity wave). If the particle is at rest in our coordinate system, it remains at rest when a gravity wave passes by. However, because the gravity wave corresponds to a deformation of the spatial coordinate lines, the proper distance between two particles at rest in the coordinate system does change (Misner et al. 1973).

Finally, the last term in the momentum equation, - w, represents a sort of cosmic drag that causes velocities of massive particles to tend toward zero in the normal (inertial) frame (by driving p toward - Ew). The timescale for this term (the time over which changes appreciably) is the Hubble time, so it should not be regarded as the frame dragging normally spoken of when loosely describing the vector mode. In fact, in the normal frame this term is absent, but then the gravitomagnetic term changes from v × H to (w ^. v). The relative velocity of the comoving and normal (inertial) frames w is responsible for the frame-dragging and other effects; let us consider a particularly interesting one.

In general, w varies with position so that at different places the inertial frames rotate relative to the comoving frame with angular velocity - 1/2 × w = - 1/2H; this is easily shown from a first-order Taylor series expansion of w with the constraint ^. w = 0. As a result, a spin S will precess relative to the comoving frame at a rate dS / d = - 1/2H × S (the Lense-Thirring effect). Using the magnetic analogy, one would predict a gravitomagnetic precession rate S × H in the comoving frame, where is the gyrogravitomagnetic ratio. (The analogous magnetic precession rate is µ × B, where µ = S.) Note that this result leads to the conclusion that there is a universal gyrogravitomagnetic ratio = 1/2!

Thus, one may interpret the vector mode perturbation variable w either as a source for (rather mysterious) frame-dragging effects, or as a vector potential for the gravitomagnetic field H. In the former case one can eliminate w altogether by choosing orthogonal space and time coordinates such as given by the synchronous gauge. However, I prefer the latter interpretation because of the close analogy it brings to electrodynamics, allowing us to transfer our flat spacetime intuition to general relativity. The price to pay is that one must be careful to distinguish the comoving and normal frames.

We have discussed the gravitomagnetic and gravitational wave contributions to the equations of motion in order to illustrate the similarities and differences between gravity and electrodynamics. (They are clearest in the Poisson gauge; the interested reader may wish to rederive the results of this section in synchronous or some other gauge.) Why aren't we familiar with these forces in the Newtonian limit? The answer is because the sources of H and h are smaller than the source of the "gravitostatic" field - by O(v/c) and O(v/c)², respectively (cf. eqs. 4.62 and 4.55). From eqs. (4.70), the forces they induce are smaller by additional factors of O(v / c) and O(v / c)². Thus, for nonrelativistic sources and particles, the dynamical effects of gravitomagnetism and gravitational radiation are negligible. While ordinary magnetic effects are suppressed by the same powers of v/c, the existence of opposite electric charges leads in most cases to a nearly complete cancellation of the electric charge density but not the current density. No such cancellation occurs with gravity because energy density is always positive.

Since typical gravitational fields in the universe have ~ 10^-5 and h_ij is much smaller than this, the curvature factors (1 + + - h) and (1 - + h) may be replaced by unity to high precision in eqs. (4.70) (and they are absent anyway in locally flat comoving coordinates). In the weak-field and slow-motion limit, then, eqs. (4.70) reduce to the standard Newtonian equations of motion in comoving coordinates.