4.9. Lagrangian field equations

General relativity makes no fundamental distinction between time and space, although we do. To obtain field equations that are similar to those of Newtonian gravity and electrodynamics, we have until now employed a "3+1 split" of the Einstein and energy conservation equations. Ellis (1971, 1973), following earlier work of Ehlers (1961, 1971), Kundt & Trümper (1961), and Hawking (1966), has developed an alternative approach based on a "1+3 split" of the Bianchi and Ricci identities. The cosmological applications have been developed extensively by Ellis and others in recent years (Ellis & Bruni 1989; Hwang & Vishniac 1990; Lyth & Stewart 1990; Bruni, Dunsby & Ellis 1992; and references therein). Ellis' approach has some important advantages, as we shall see.

The 3+1 split corresponds to the "slicing" of spacetime into a series of spatial hypersurfaces, each labeled by a coordinate time . (The different splitting procedures are most easily visualized with one spatial dimension suppressed using a 2+1 spacetime diagram, with time corresponding to the vertical axis. The spatial hypersurfaces are then horizontal slices through spacetime.) Spacetime is described by Eulerian observers sitting in these hypersurfaces with constant spatial coordinates.

The 1+3 split, called "threading," is complementary to slicing (Jantzen et al. 1992). In this case the fundamental geometrical objects used for charting spacetime are a series of timelike worldlines x^µ(;q), where is an affine parameter measuring proper time along the worldline and q gives a unique label (e.g., a spatial Lagrangian position vector) to each different worldline (or "thread"). In this case spacetime is described by Lagrangian observers moving along these worldlines.

The threading description is more general than the slicing one. If we take the threads to correspond to the worldlines of comoving observers in the slicing framework (lines of fixed x), then the two descriptions are the same. In the 1+3 description, however, different threads may cross with no harmful consequences while in the 3+1 description a spatial hypersurface must not be allowed to cross itself or other slices. Thus, the threading description may be used to follow the evolution of cold dust beyond the time when matter trajectories intersect, when the perfect-fluid Euler equations break down. The advantage of a Lagrangian description is well known for collisionless matter - the Lagrangian approach exclusively is used for nonlinear gravitational simulations -- and the same advantages accrue even when describing the spacetime geometry itself.

In the 1+3 approach each worldline threading spacetime has a timelike unit tangent vector (4-velocity) u^µ = dx^µ / d = u^µ(; q) such that u^µu_µ = - 1. Spacetime tensors are then decomposed into parts parallel and normal to the worldline passing through a given point. This decomposition is accomplished in a covariant form using the tangent vector u^µ and the orthogonal projection tensor

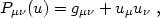(4.71)

such that P_µ u = 0 and P^µ P = P^µ. P_µ is effectively the spatial metric for observers moving with 4-velocity u^µ (Ellis 1973). We may use it and u^µ to split any 4-vector A^µ into timelike and spacelike parts, labeled by the tangent vector of the appropriate thread:

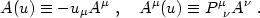(4.72)

Even though A^µ(u) looks like (and is, in fact) a 4-vector, we can regard it as a 3-vector in the rest frame of an observer moving along the worldline x^µ(; q) because u_µA^µ(u) = 0. [Note that A^µ denotes the original 4-vector while A^µ(u) denotes its projection normal to u^µ. We shall include the argument (u) for the projection whenever needed to remove ambiguity.] We require that at each point in spacetime there is at least one thread with corresponding tangent u^µ(; q). If there are several threads then there are several different decompositions of A(u) and A^µ(u) at x^µ, each labeled by q (implicitly, if not explicitly) through u^µ(; q). This causes no problems as long as we refer to a single distinct thread, which we do by retaining u in the argument list.

The decomposition of a second-rank tensor T^µ is similar:

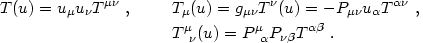(4.73)

As an exercise one may apply this decomposition to the stress-energy tensor of eq. (4.19) using the comoving observers to define the threading. For v² << 1, one obtains nonzero elements T = , T_i = a( + p)v_i (with no w_i), and Tⁱ_j = p_jⁱ + _jⁱ. Be careful to distinguish the 4-velocity of the threads (with vⁱ = 0) from those of the matter (eq. 4.22).

Now that we have described the 1+3 spacetime splitting procedure, we are ready to apply it to gravity following Hawking (1966) and Ellis (1971, 1973). What equations should we use? One might think to split the Einstein equations using 1+3 threading, but this does not add anything fundamentally new to what we have already done. The correct approach suggests itself when we think in Lagrangian terms following a freely-falling observer, whose worldline defines one of the threads. Such an observer feels no gravitational force at all but does notice that adjacent freely-falling observers do not necessarily move in straight lines with constant speed. In Newtonian terms this is explained by "tidal forces" while in general relativity it is called geodesic deviation. We shall not present a derivation of geodesic deviation here (one may find it in any general relativity textbook) but simply note that it follows from the non-commutativity of covariant spacetime derivatives of the 4-velocity. The relevant equation is the 4-dimensional version of the first of eqs. (4.5), called the Ricci identity:

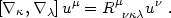(4.74)

This identity holds for any differentiable vector field u^µ. In the Lagrangian field approach we seek evolution equations for the Riemann tensor itself rather than the metric tensor components.

One advantage of working with the Riemann tensor is the fact that part of it - the Ricci tensor - is given algebraically by the local stress-energy through eqs. (4.7) and (4.8). However, one cannot (in 4 dimensions) reconstruct the entire Riemann tensor from the Ricci tensor alone. One could obtain it by differentiating the metric found by solving the Einstein equations (cf. eqs. 4.9, 4.10). As we shall see, there is another method that does not require integrating the Einstein equations.

This alternative method is based on an evolution equation for that part of the Riemann tensor that cannot be obtained from the Ricci tensor, the Weyl tensor C_µ:

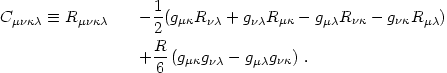(4.75)

This tensor obeys all the symmetries of the Riemann tensor - C_µ = C_{[µ] []} = C_µ and C_µ[] = 0 (where square brackets denote antisymmetrization) - and in addition is traceless: C_µ = 0. Thus, the trace part of the Riemann tensor is given by the Ricci tensor R_µ (through the Ricci terms on the right-hand side of eq. 4.75) while the traceless part is given by the Weyl tensor. Physically, the Ricci tensor gives the contribution to the spacetime curvature from local sources (through the Einstein eqs. 4.7 combined with 4.8) while the Weyl tensor gives the contribution due to nonlocal sources. It is clear that Newtonian tidal forces will be represented in the Weyl tensor. It may be shown that in 4 dimensions the Ricci and Weyl tensors each have 10 independent components.

How do we get an evolution equation for the Weyl tensor? The Einstein equations will not do because the Weyl tensor makes no appearance at all in the Einstein tensor. The correct method, due to Kundt & Trümper (1961), makes use of the Bianchi identities,

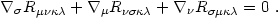(4.76)

These identities follow directly from the definition of the Riemann tensor (see any general relativity or differential geometry textbook). For our purposes the key point is that they provide differential equations for the Riemann tensor. Contracting eq. (4.76) on and and using eqs. (4.75) and (4.8), we get

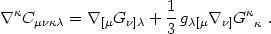(4.77)

Note that if we contract now on and µ, using the symmetry of G_µ and g_µ we get _µ G^µ = 0, as noted before. However, here we regard eq. (4.77) as an equation of motion for the Weyl tensor. Using the Einstein eqs. (4.7), we see that the source is given in terms of the energy-momentum tensor, so

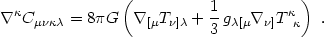(4.78)

The next step is to split the Weyl tensor into two second-rank tensors using a 1+3 threading of spacetime (Hawking 1966, Ellis 1971),

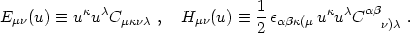(4.79)

We have used the fully antisymmetric tensor _µ = (- g)^1/2 [µ], where g is the determinant of g_µ and [µ] is the completely antisymmetric Levi-Civita symbol defined by three conditions: (1) [0123] = + 1, (2) [µ] changes sign if any two indices are exchanged, and (3) [µ] = 0 if any two indices are equal. (Note that Ellis uses the tensor _µ = - _µ. We have compensated for the sign change in defining H_µ. Beware that ^µ = - (- g)^-1/2[µ].) The two new tensors E_µ and H_µ are both symmetric (H_µ must be explicitly symmetrized), traceless, and flow-orthogonal, i.e., E_µ u = H_µ u = 0 and P E_µ = E_µ, P H_µ = H_µ. Therefore E_µ and H_µ each has 5 independent components, half as many as the Weyl tensor. Indeed, the Weyl tensor is fully determined by them for non-null threads:

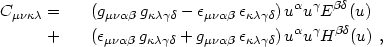(4.80)

where g_µ g_µ g - g_µ g = - 1/2_µ = g_[µ][] = g_µ, with g_µ[] = 0. Eq. (4.80) is the inverse of eqs. (4.79) provided g_µ u^µ u = ±1. Ellis (1971) has a sign error in the first term of his version of eq. (4.80) at the end of his section 4.2.3.

The tensors E_µ(u) and H_µ(u) are called the electric and magnetic parts of the Weyl tensor, respectively. Together with the Ricci tensor they fully determine the spacetime curvature for a given threading (i.e., a system of threads with tangent vectors) u^µ(; q). It is worth noting that, if there are several threads at a given spacetime point, E_µ(u) and H_µ(u) have different values for each thread, and so they may be considered Lagrangian functions: E_µ(; q) and H_µ(;q). The Weyl tensor components are, however, unique, with the same value for all threads passing through the same spacetime point. This condition is satisfied automatically if the same 4-velocity u^µ is used in both eqs. (4.79) and (4.80).

Our goal is to rewrite eq. (4.78) in terms of E_µ and H_µ. Because the results involve the covariant derivative of the 4-velocity field _µ u, we first decompose this quantity into acceleration, expansion, shear, and vorticity:

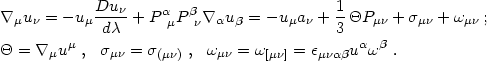(4.81)

We have introduced the covariant derivative in the direction u, D / d u. Since this is just the proper time derivative along the worldline, a = Du / d is the 4-acceleration. The flow-orthogonal part of the velocity gradient, P_µ P u, has been decomposed into the expansion scalar , the traceless shear tensor _µ, and the vorticity tensor _µ or its flow-orthogonal dual, ^µ. Note that the expansion scalar includes a contribution due to cosmic expansion in addition to the peculiar velocity: neglecting metric perturbations, = a^-1( + ^. v). Note also that in the fluid rest frame, ⁱ e_i = 1/2 × v is half the usual three-dimensional vorticity. (Ellis defines _µ and ^µ with the opposite sign to us.)

We shall apply this gradient expansion to the tangent field of the 1+3 spacetime threading. This requires that u^µ be differentiable, which will be true (almost everywhere) if it corresponds to the 4-velocity field of a flow. In a frame comoving with the fluid, , _ij and _ij are then the usual fluid expansion, shear, and vorticity, respectively.

By projecting C_µ with various combinations of u and P(u) (these are dependent on the spacetime threading), one can derive the following identities:

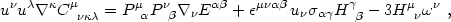(4.82)

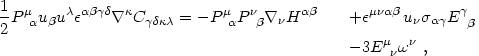(4.83)

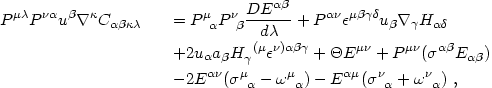(4.84)

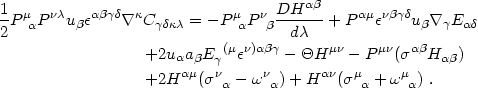(4.85)

These identities follow from eqs. (4.80) and (4.81) All quantities on the right-hand sides are to be evaluated for a given thread u^µ(; q).

Finally we are ready to obtain equations of motion for the electric and magnetic parts of the Weyl tensor from eq. (4.78). In fact, infinitely many sets of equations are possible because are free to use any spacetime threading! For example, we may choose Eulerian threading with q = x, in which case in the Poisson gauge we have u⁰ = a^-1(1 - ) and uⁱ = 0, so that D/d = a^-1(1 - ) is the Eulerian proper time derivative. In this case the 1+3 split coincides with our previous 3+1 split. The Eulerian description is not covariant, for it depends on our choice of gauge. Because the Weyl tensor formalism is more complicated than our previous treatment based on the Einstein equations, there is no clear advantage to its use with Eulerian threading.

If, however, we use the fluid velocity itself - the u^µ appearing in eq. (4.19), which is well-defined even for an imperfect or collisionless fluid - to define the threading, then the Weyl tensor approach becomes more attractive. This choice corresponds to Lagrangian threading: the threads are the worldlines of fluid elements, so that D / d now is the proper time derivative measured in the fluid rest frame. There are two important advantages to this choice. First, it is covariant: the fluid worldlines define a unique spacetime threading with no gauge ambiguities (Ellis & Bruni 1989), while any coordinates may be used to express the tensor components E_µ and H_µ. Second, the right-hand side of eq. (4.78) - the source for the Weyl tensor - is expressed in terms of the same 4-velocity used in the threading, greatly simplifying the projections appearing in eqs. (4.82)-(4.85).

Ellis (1971) and Hwang & Vishniac (1990) give the Lagrangian gravitational field equations for a general stress-energy tensor. For a perfect fluid (with ^µ = 0 in eq. 4.19) the results are

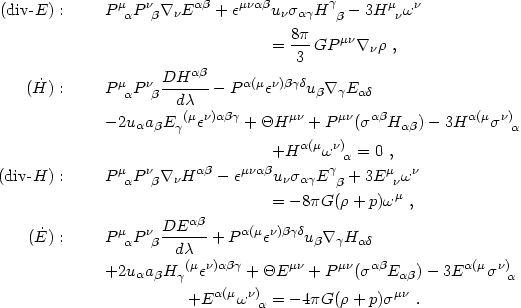(4.86) (4.87) (4.88) (4.89)

These have been obtained by substituting eqs. (4.19) and (4.82)-(4.85) into eq. (4.78), and using T^µ = 0 to simplify the right-hand sides of the div-E and 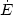equations. The results agree with eqs. (4.21) of Ellis (1971). For an imperfect fluid it is necessary to add terms to the right-hand sides involving the shear stress ^µ. For a pressureless fluid (e.g., cold dust before the intersection of trajectories) the 4-acceleration a vanishes.

In his beautifully lucid pedagogical articles presenting the Lagrangian fluid approach, Ellis (1971, 1973) has noted the similarity of eqs. (4.86)-(4.89) to the Maxwell equations, particularly if the covariant form of the latter are split using 1+3 threading. Compare them with eqs. (4.62) for the vector (not tensor) gravitational fields in the Poisson gauge. Although the latter equations are more reminiscent of the Maxwell equations in flat spacetime, they are only approximate (they are based on a linearized metric and neglect several generally small terms), they are tied to a particular coordinate system (Poisson gauge), and they do not incorporate gravitational radiation. By contrast, eqs. (4.86)-(4.89) are exact, they are valid in any coordinate system (all quantities appearing in them are spacetime tensors), and they include all gravitational effects. The exact equations involve second-rank tensors rather than vectors because, in the terminology of particle physics, gravity is a spin-2 rather than a spin-1 gauge theory.

The quasi-Maxwellian equations (4.86)-(4.89) show that the evolution of the Weyl tensor depends on the fluid velocity gradient. This quantity could be computed by evolving the equations of motion for the matter (e.g., eqs. 4.24 and 4.25) to get the velocity field u^µ(x) and then taking its derivatives. However, there is a more natural way in the context of the Lagrangian approach: integrate evolution equations for the velocity gradient itself. In fact, such equations follow simply from projecting the Ricci identity (4.74) for the fluid velocity u^µ with u P P_µ and separating the result as in eqs. (4.81). It is straightforward to derive the following equations (Ellis 1971, 1973):

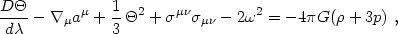(4.90)

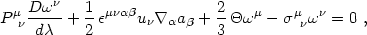(4.91)

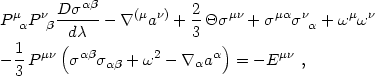(4.92)

where ^{2 µ} _µ. Equation (4.90) is known as the Raychaudhuri equation. It shows that the expansion is decelerated by the shear and by the local density and pressure (if + 3p > 0), but is accelerated by the vorticity. Vorticity, on the other hand, is unaffected by gravity; eq. (4.91) implies that vorticity can be described by field lines that (if a^µ vanishes or if the fluid has vanishing shear stress) are frozen into the fluid (Ellis 1973). Finally, shear, being the traceless symmetric part of the velocity gradient tensor, has as its source the electric part of the Weyl tensor. These equations are essentially identical to their Newtonian counterparts (Ellis 1971; Bertschinger & Jain 1994). Note that the magnetic part of the Weyl tensor does not directly influence the matter evolution.

Closing the Lagrangian field equations also requires specifying the evolution of density and pressure (and shear stress, if present). These follow from energy conservation, T^µ = 0, combined with an equation of state. For a perfect fluid, using eq. (4.19) with ^µ = 0 and projecting the divergence of the stress-energy tensor with u_µ gives

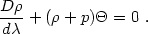(4.93)

Equations (4.86)-(4.93) now provide a set of Lagrangian equations of motion for the matter and spacetime curvature variables following a mass element. These Lagrangian equations of motion offer a powerful approach to general relativity - and to relativistic cosmology and perturbation theory - that is quite different from the usual methods based on integration of the Einstein equations in a particular gauge (or with gauge-invariant variables).

To relate the relativistic Lagrangian approach to dynamics to the standard Newtonian one, we now evaluate the electric and magnetic parts of the Weyl tensor in the weak-field, slow-motion limit. They involve second derivatives of the metric and not simply the first derivatives present in eqs. (4.61). In the Poisson gauge, to lowest order in the metric perturbations and the velocity, from eqs. (4.79) one obtains (Bertschinger & Hamilton 1994)

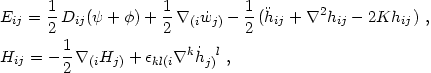(4.94)

where H_j is the gravitomagnetic field defined in eq. (4.61). The time-time and space-time components of E_µ and H_µ vanish in the fluid frame because these tensors are flow-orthogonal.

Do these results imply that in the Newtonian limit H_ij = 0 and E_ij = D_ij is simply the gravitational tidal field? If we say that the Newtonian limit implies = and w_i = h_ij = 0 (no relativistic shear stress, no gravitomagnetism, and no gravitational radiation), then the answer would appear to be yes. This possibility, considered by Matarrese, Pantano, & Saez (1993) and Bertschinger & Jain (1994), has an important implication: for cold dust, the Lagrangian evolution of the tidal tensor obtained from eq. (4.89) would then be purely local (Barnes & Rowlingson 1989). That is, the evolution of the tide (the electric part of the Weyl tensor) along the thread u^µ(; q) would depend only on the density, velocity gradient, and tide defined at each point along the trajectory with no further spatial gradients (since they arise only from the magnetic terms in eq. 4.89). The evolution of the density and of the velocity gradient tensor are clearly local (eqs. 4.90-4.93, with a^µ = 0) aside from the tidal tensor, but we have just seen that its evolution depends only on other local quantities. In other words, if H_ij = 0, the matter and spacetime curvature variables would evolve independently along different fluid worldlines. Bruni, Matarrese, and Pantano (1994) call this a "silent universe."

Local evolution does occur if the metric perturbations are one-dimensional (e.g., the Bondi-Tolman solution in spherical symmetry, or the Zel'dovich solution in plane symmetry; see Matarrese et al. 1993 and Croudace et al. 1994), but it would be surprising were this to happen for arbitrary matter distributions in the Newtonian limit.

Bertschinger & Hamilton (1994) and Kofman & Pogosyan (1995) have shown that, in fact, the general evolution of the tidal tensor in the Newtonian limit is nonlocal. The reason is that, while one may neglect the metric perturbation w_i in the Newtonian limit, its gradient should not be neglected. Doing so violates the transverse momentum constraint equation (4.51), unless the transverse momentum density (the source term for w in the Poisson gauge) vanishes. This condition does not hold for general motion in the Newtonian limit.

A convincing proof of nonlocality is given by the derivation of eq. (4.89) in locally flat coordinates in the fluid frame by Bertschinger & Hamilton (1994) using only the Newtonian continuity and Poisson equations plus the second pair of eqs. (4.62) and a modified form of eq. (4.94):

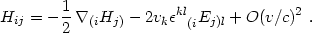(4.95)

This is taken as the definition of H_ij in the Newtonian limit (where we also have E_ij = D_ij ). Note that in the Newtonian limit we neglect gravitational radiation, but we must include terms that are first-order in the velocity. Even though we define the magnetic part of the Weyl tensor using the fluid 4-velocity, we are evaluating its components in a particular gauge - Poisson gauge - in which the 3-velocity does not necessarily vanish. The extra term in eq. (4.95) arises from evaluating eqs. (4.79) to first order in v/c (Bertschinger & Hamilton 1994) and it is analogous to the Lorentz transformation of electric fields into magnetic fields in a moving frame. Both terms in eq. (4.95) are of order G v. They can not be neglected in the Newtonian limit.

The implication of this result is that Lagrangian evolution of matter and gravity is not purely local except under severe restrictions such as spherical or plane symmetry. There exist, of course, local approximations to evolution such as the Zel'dovich (1970) approximation. Finding improved local approximations is one of the active areas of research in large-scale structure theory. Formulating the problem in terms of the Lagrangian fluid and field equations not only may suggest new approaches, it is also likely to clarify the relation between general relativity and Newtonian dynamics.