3. COMPACT RADIO COMPONENTS

3.1. Angular size constraints

As with the extended sources, the primary radio emission is usually attributed to synchrotron radiation by relativistic electrons in a partially ordered field, although alternatives have been investigated. The evidence for this is perhaps not so good as in the extended sources, as the observed degrees of polarisation are much lower; however the majority of the sources can be satisfactorily interpreted using this hypothesis [26].

The source energetics are critically dependent on the angular size , which can be estimated in several different ways. As described by Dr Kellerman, VLBI can provide angular information on milliarcsecond structure, which can (with the aid of a cosmological model) be converted into a linear size and shape; and an expansion speed that apparently often exceeds c. Searches for interstellar scintillation, as yet undetected, provide lower limits on in the range ~ 1 - 10 microarcsecond.

Secondly, and especially for sources that are too weak for VLBI, an upper limit on the angular size can be set from the variability timescale _var (ignoring kinematic effects discussed below).

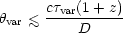
(4)

where D is the luminosity distance to the source (D = H₀^-1 q₀^-2[z q₀ + (1 - q₀)(1 - sqrt{1 + 2 q₀ z})] in a Friedmann cosmology).

Thirdly, in some sources a low-frequency turnover, interpretable as synchrotron self-absorption, yields an estimate of the brightness temperature and hence of the angular size. (If a turn-over is not observed, the synchrotron hypothesis leads to a lower limit on the angular size.) Essentially the limit arises because when the source becomes self-absorbed the radiation brightness temperature S ^-2 is comparable with the kinetic temperature of the electrons ( (v_n / B)^1/2) emitting at the frequency v_n where the flux turns over. Numerically,

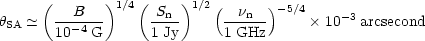
(5)

where S_n = S(_n). More detailed expressions correcting for cosmological and spectral effects are given by Jones, O'Dell and Stein [27]. More serious modifications are required with alternative radiation processes. For example with proton synchrotron radiation the brightness temperature in a source of fixed size and field strength is increased by ~ (m_p / m_e)^1/2 but only at the expense of imposing severe constraints on the relativistic electron density [28]. With inverse Compton scattering, the brightness temperature is decreased. Coherent mechanisms of course permit still higher temperatures.

A fourth limit on the angular size comes from considering the consequences of inverse Compton scattering of the radio photons by the same electrons that produced them. If the radiation energy density U_rad exceeds the magnetic field energy density B² / 8, then a relativistic electron will lose more energy producing Compton photons, typically in the infrared or optical range, than radio. These Compton photons can themselves be scattered, and so on until their unscattered frequency satisfies h m_e c² with the Lorentz factor of the electron that produced the original radio photon. At these frequencies, electron recoil is important and the cross-section is diminished, thus suppressing further scattering. Large Compton fluxes are undesirable for two reasons: they greatly increase the energy requirements of the source and they may come into conflict with existing observational upper limits, particularly at X-ray energies. This therefore implies that U_rad B² / 8.

If we assume that the radiation is produced in a homogeneous spherical source of angular diameter , and that S() is maximised at some frequency _u with flux S(_u), typically in the mm range, then this condition becomes

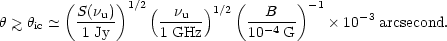
(6)

Strictly, we have no guarantee that the flux S_u arises from the same location and at the same time as S_n and so we can obtain a definite lower bound on the angular size by equating _n with _u

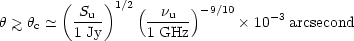
(7)

or equivalently in terms of the observed brightness temperature, T_n 10¹² K [29]. (It is a curious coincidence that this is about the maximum brightness temperature that can be detected from a ~ 1 Jy source using VLBI with an intercontinental baseline.)

As discussed in detail by Burbidge, Jones and O'Dell [26], and by O'Dell [30], the angles _VLB, _var and _c are in general comparable, although the upper limit _var tends to be smaller than _VLBI and the lower limit _c tends to be larger. This encourages confidence in the electron synchrotron hypothesis. A second conclusion is that generally B_eq > B_c, and so the particle pressure exceeds the magnetic stresses. It is in general impossible to derive precise estimates of magnetic field strengths, energy contents, etc because all such quantities depend on very high powers of .

The estimated energy content of compact components is sometimes as large as ~ 10⁵⁶ erg, assuming isotropic emission. These estimates (which are larger than could be obtained from a single supernova-style explosion) could be reduced by adopting some special geometry. But they are in any case much smaller than the energies involved in extended sources, which is consistent with the view that the latter are built up by nuclear activity over periods 10⁶ yr.