3.2. Radiative transfer

So far we have assumed implicitly that the observed radiation is unchanged in spectrum and polarisation from what was emitted. In fact there are a variety of propagation effects which can substantially modify the emergent radiation and indeed in some sources we can obtain important physical constraints on the conditions within and around the radio components simply from our failure to detect these changes.

Free-free absorption will effectively suppress the emission below a frequency

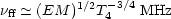
(8)

where EM = (n_e / 1 cm^-3)²(dl / 1 pc) is the emission measure of the thermal plasma, of temperature 10⁴T₄ K, along the line of sight. In those sources, e.g., associated with quasars displaying prominent emission line spectra, typical values are EM ~ 10¹², T₄ 1 and so the emitting filaments cannot completely occult the radio source.

A second (fairly unimportant) limit on the thermal electron density can be set from the manifest absence of Razin suppression of the synchrotron emission. This gives

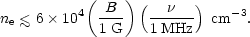
(9)

Of more interest are the limits derived from polarisation observations. Most sources display 1-10 per cent linear polarisation and 0.1 per cent circular polarisation. The fact that this much linear polarisation emerges and that its plane of polarisation does not rotate during the evolution of a source places an upper bound on the internal Faraday rotation of the source. Both thermal and relativistic electrons can contribute to the rotation and the expected depolarisation. The equation of radiative transfer has been solved in a variety of source models.

For a homogeneous source the Faraday rotation due to thermal plasma is n_eBR / v², where n_e is the thermal electron density; and the brightness temperature where the source is just optically thin is T n_relBl / v² where n_rel is the density of relativistic electrons emitting at this frequency. We can therefore obtain a limit on n_e / n_rel (3 × 10⁹ / T) independent of B, as most sources have T 10¹² K and 1 (otherwise they would be strongly depolarized). This limit is typically ~ 10^-3 - 10^-4 and is so small that the Faraday rotation due to relativistic electrons must be investigated. The rotation due to the relativistic plasma is n_relBR / v² <ln / ²>; and for the brightest sources, not showing changes in , the electron distribution function must cut off below energies ~ 10-100 MeV [31, 32].

As radio components have a typical degree of polarisation 10 per cent of the theoretical maximum for a synchrotron source (~ 70 per cent) they must exhibit some structural de-polarisation, which will increase the limits on n_e and n_rel, as the field will reverse several times along the line of sight, reducing the rotation measure. It is in principle possible to reduce to a negligible value without destroying the polarisation simply by shearing a source with small scale magnetic turbulence, but in practice this is probably difficult to maintain for any length of time since the timescale for isotropising the field is only that taken by an Alfven wave to traverse the scale of an irregularity. A second type of inhomogeneity occurs if a lot of the mass is contained in filaments that do not completely occult the source. In this case the radio-emitting plasma is probably dynamically decoupled from the filaments. The natural inference is then that the radio emitting regions contain predominantly relativistic plasma.

A circular polarisation can also be produced as a consequence of propagation through a relativistic plasma [33, 34]. This arises because the normal modes of propagation through a plasma are not purely circularly polarised; and so, by a straightforward modification of the mechanism responsible for Faraday rotation, a linearly polarised wave emitted by the synchrotron process will be partially converted into a circularly polarised wave. If the relativistic electron distribution function is a power-law with s 2 and extends down to some energy _min mc², then the expected degree of circular polarisation _c produced by radiative transfer near turnover is approximately related to the Faraday rotation by

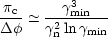
(10)

where _n mc² is the energy of electrons radiating at the turnover frequency. The sign of the circular polarisation generally reverses near turnover.

Circular polarisation is also produced intrinsically in the synchrotron process [35 - 37] and it too reverses near turnover. The expected magnitude is

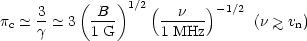
(11)

In an inhomogeneous source these estimates must be reduced like . _c can in principle be reduced to a negligible value without seriously diminishing the linear polarisation.

Reported values of _c are in the range 0.1-1 per cent. If reliable upper limits < 0.1 per cent turn out to be very common, then they are probably too small to be understood in terms of a relativistic electron synchrotron source, and one intriguing possibility is that the source comprise equal numbers of electrons and positrons. If observations could be pushed to the point where this seemed the most attractive solution, then it would have important consequences for isolating the particle acceleration mechanism. The sources where one might expect detectable circular polarisation are those such as the low-power compact component of 3C 84 where the field may be 0.1 G.

Another propagation effect that can profoundly influence the character of the emergent radiation is induced Compton scattering. If we consider scattering off free electrons, then induced scatterings [38, 39] are more important than spontaneous scatterings if the brightness temperature T exceeds m_ec² / k 10¹⁰ K. (The rate of induced scattering out of a photon state exceeds the spontaneous rate by a factor of order the photon occupation number ~ kT / h. However there are also induced scatterings into this state and so the net induced scattering rate is reduced by the relative Compton shift, / (h / m_ec²)). Typical brightness temperatures are T 10¹² K and so if the optical depth to spontaneous Thomson scattering, _T traversed by the emergent radiation lies in the range 10^-2 _T 1, then induced effects can influence the spectrum without increasing the source size by spontaneous scattering. (It is necessary that the thermal plasma be close to the source as the induced scattering rate ⁴ where is the angle subtended by the source [40, 41]. This is because induced scatterings only occur between states that contain a high number of photons already. As the photons are "hotter" than the thermal plasma they will fall in frequency whilst conserving their total number, and if (kT / m_ec²) _T² 1 the spectrum will be severely distorted. Linear polarisation can also be created and destroyed by this mechanism [41]. However, comparison with eq. (8) shows that free-free absorption at ~ 1 GHz in a source of size ~ 1 pc is likely to occur before induced scattering unless the electron temperature is 10⁵ K. (If free-free absorption became important it would in any case raise the temperature [42].) A second constraint on the physical conditions in such a scattering region is that the magnetic field strength be much less than in the source in order that the Faraday rotation not be greater than observed.