


2.4.2. Correlation functions
An alternative to the morphological approach described above is to use statistics. Statistical analyses of galaxy catalogues have been considered by various authors (Rubin, 1954; Limber, 1954; Neyman, Scott and Shane, 1954; Totsuji and Kihara, 1969) though much of the recent interest has been due to the results of Peebles and coworkers. Peebles et al. have applied the low-order correlation functions as a measure of galaxy clustering to the Zwicky, Lick and Jagellonian galaxy catalogues. This work has been reviewed extensively by Fall (1979a) and Peebles (1980a), to which we refer the interested reader for details; here we shall briefly discuss the main results.
The two-point correlation function
 (r) is
defined so that the joint
probability of finding galaxies in the volume elements
(r) is
defined so that the joint
probability of finding galaxies in the volume elements
 V1,
V1,
 V2
separated by a distance r is
V2
separated by a distance r is
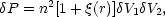 |
(2.25) |
where n is the mean space density of galaxies. Hence
 (r) measures
deviations of the pattern of galaxy clustering from a Poisson
distribution. The data available to Peebles et al. has consisted of
galaxy coordinates in projection. Hence in order to estimate the form
of
(r) measures
deviations of the pattern of galaxy clustering from a Poisson
distribution. The data available to Peebles et al. has consisted of
galaxy coordinates in projection. Hence in order to estimate the form
of  (r)
they have measured the angular two-point function
w(
(r)
they have measured the angular two-point function
w( ).
w(
).
w( )
is defined in an exactly analogous way to
)
is defined in an exactly analogous way to
 (r) and is
related to
(r) and is
related to  via
an integral equation first derived by
Limber (1954).
Higher order
correlation functions may also be defined, e.g. the three-point
function
via
an integral equation first derived by
Limber (1954).
Higher order
correlation functions may also be defined, e.g. the three-point
function  :
:
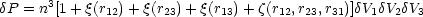 |
(2.26) |
where  P is the
joint probability of finding galaxies in each of the
three volume elements
P is the
joint probability of finding galaxies in each of the
three volume elements
 V1,
V1,
 V2,
V2,
 V3 with
separations r12, r23,
r13.
Similarly, the four-point and higher order correlations may be
defined, though so far useful results have not been obtained for
correlation functions of higher order than the four-point function.
V3 with
separations r12, r23,
r13.
Similarly, the four-point and higher order correlations may be
defined, though so far useful results have not been obtained for
correlation functions of higher order than the four-point function.
The main result (Peebles, 1974a) is that the spatial two-point correlation function has an approximately power law from over a wide range of scales,
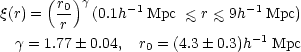 |
(2.27) |
The normalization factor, r0, quoted here comes from Peebles' analysis of the Kirshner et al. (1978) redshift sample (Peebles, 1979) and the formal error may be an underestimate because of sampling problems. In a revised analysis of the Lick catalogue, Groth and Peebles (1977) report the existence of a sharp break from the power law (2.27) at a value of approximately
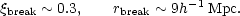 |
Thus there appears to be negligible clustering on scales
> rbreak. This
result is rather tentative as the analysis may be subject to
systematic errors, though a similar feature has been found from deeper
galaxy samples
(Shanks et al., 1980).
Gott and Turner (1979)
have extended the correlation function analysis for the Zwicky catalogue
down to small separations using the accurate positions of binary pairs
in Turner's (1976)
catalogue. They find the new data to be consistent
with the extrapolation of Eq. (2.27) to very small scales,
r  5h-1 kpc.
5h-1 kpc.
In addition to these results, Peebles and Groth (1975) have discovered that the three-point correlation function has the following simple analytic form,
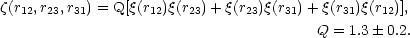 |
(2.28) |
Equation (2.28) is found to be a good representation of the data over
the range of scales 0.1h-1 Mpc
 r
r
 2h-1 Mpc.
Fry and Peebles (1978)
have estimated the four-point function
2h-1 Mpc.
Fry and Peebles (1978)
have estimated the four-point function
 which is
consistent with the
generalization of (2.28) to a sum of triple products of
which is
consistent with the
generalization of (2.28) to a sum of triple products of
 . Several
other results have been obtained by Peebles and coworkers, such as
cross-correlations between galaxies and other extragalactic objects
but these will not be discussed here. One result worth mentioning,
however, concerns the two-point correlation function of rich clusters
of galaxies
. Several
other results have been obtained by Peebles and coworkers, such as
cross-correlations between galaxies and other extragalactic objects
but these will not be discussed here. One result worth mentioning,
however, concerns the two-point correlation function of rich clusters
of galaxies
 cc.
Hauser and Peebles (1973)
find that rich clusters are
more strongly correlated than galaxies, with
cc.
Hauser and Peebles (1973)
find that rich clusters are
more strongly correlated than galaxies, with
 cc
cc
 10
10
 (r).
(5) Thus rich
clusters and galaxies cannot both be good tracers of the mass
distribution.
(r).
(5) Thus rich
clusters and galaxies cannot both be good tracers of the mass
distribution.
The relations between the two-point and higher order correlation
functions suggest that galaxies are grouped in a nested clustering
hierarchy. If we look at the clustering pattern with a resolution r,
typical clumps of galaxies will have an overdensity with respect to
the background 
 /
/
 ~
~
 (r).
The mean number of neighbours per unit
volume at a distance r from a randomly chosen galaxy will scale as
n(r)
(r).
The mean number of neighbours per unit
volume at a distance r from a randomly chosen galaxy will scale as
n(r) 

 , thus the model
predicts that the three-point correlation
function should scale according to Eq. (2.28) with
, thus the model
predicts that the three-point correlation
function should scale according to Eq. (2.28) with


 2
(Peebles and Groth, 1975).
2
(Peebles and Groth, 1975).
Clumps with a high overdensity should be bound and stable in which
case one can apply the virial theorem. The mass of a typical clump is
M ~ 
 r3, hence the internal velocities should scale
with clump size as
r3, hence the internal velocities should scale
with clump size as
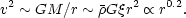 |
(2.29) |
A more rigorous version of this argument has been given by Peebles (1976a, b). The one-dimensional mean square relative peculiar velocity <v212> between pairs of separation r12 is related to the sum of the accelerations over triplets of galaxies,
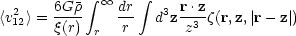 |
(2.30) |
if the velocity distribution is isotropic and the clustering is bound and stable. Using Eqs. (2.28) and (2.27), Eq. (2.30) may be written
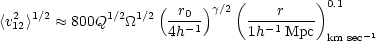 |
(2.32) |
This relation is sometimes called the "cosmic" virial theorem and
agrees with the simple application of the virial theorem which led to
Eq. (2.29). Thus a measure of the relative peculiar velocities
between galaxy pairs provides an estimate of the cosmological density
parameter provided that the galaxy correlation functions accurately
measure the mass distribution. The scaling of
<v212> with pair
separation provides a check of this point, for Eq. (2.32) predicts
that <v212> should be very nearly
independent of scale.
Fall (1975)
has derived a relation between the mean-square peculiar velocities of
single galaxies and the two-point correlation function which, in
principle, can be used to estimate
 . Unfortunately,
Fall's method is sensitive to the shape of
. Unfortunately,
Fall's method is sensitive to the shape of
 (r) at
large separations.
(r) at
large separations.
Several applications of the cosmic virial theorem may be found in the literature (Peebles, 1976b; Davis, Geller and Huchra, 1978; Peebles, 1979, 1980b). The most extensive results come from the Center for Astrophysics redshift survey (Davis and Peebles, 1983) and the deep redshift survey of Bean et al. 1983. These surveys suggest
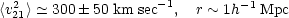 |
(2.33) |
with a weak dependence on pair separation consistent with Eq. (2.32). Applying the cosmic virial theorem using Q = 1.3 (Eq. 2.28) gives,
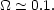 |
(2.34) |
Thus, the relative peculiar velocities suggest a low mean matter
density. Comparing with Eq. (2.24) we find a mean mass-to-light ratio
of ~ 50h(M/L) which is similar to the
results obtained from
application of the virial theorem to groups but somewhat less than the
results from the cores of rich clusters (e.g.
Rood et al. 1972).
which is similar to the
results obtained from
application of the virial theorem to groups but somewhat less than the
results from the cores of rich clusters (e.g.
Rood et al. 1972).
The results do not necessarily exclude a high density universe for it is possible that most of the dark material is in a broadly distributed component that is not highly clustered on small scales. The present redshift samples are too small to check this point.
5 See the recent extensive discussion of this point by Bond and Szalay (1983). Back.