3.1. Linear perturbations

For simplicity, in the following discussion we will restrict attention to the case of an Einstein-de Sitter (k = 0) model composed of radiation, considered as a perfect fluid with an equation of state p = 1/3 c², together with a pressureless baryon fluid. These conditions are easily relaxed but represent an adequate approximation to the standard hot big bang models during the radiation era and whilst perturbations on scales corresponding to galaxies and galaxy clusters are larger than the particle horizon.

The unperturbed metric may be written as ⁽⁶⁾

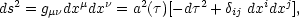(3.1)

and the unperturbed energy momentum tensor

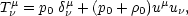(3.2)

where p₀ is the unperturbed pressure and ₀ is the unperturbed energy density and the four velocity u^µ has components

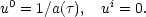(3.3)

The scale factor a() is related to p₀ and ₀ by the usual Friedmann equations (Weinberg, 1972, Section 15),

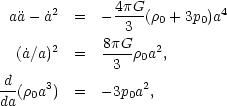(3.4a) (3.4b) (3.4c)

where a dot denotes a derivative with respect to . In addition, let

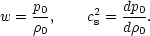(3.5)

Now, consider the perturbed metric,

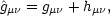(3.6)

where the perturbations are assumed to be small | h_µ| << a²(). Since the h_µ are not physically measurable quantities one may make an infinitesimal coordinate transformation,

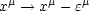(3.7)

to find an equally valid solution

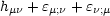(3.8)

(Weinberg, 1972, Section 15.10). The ability to add terms to h_µ which correspond merely to infinitesimal (gauge) transformations has led to some problems in the interpretation of the results of the perturbation calculations. In particular since the quantity of most interest, the fractional change in energy density = / ₀, is not a gauge invariant quantity, various results for the growth rates of may be found in the literature (Lifshitz, 1946; Harrison, 1967; Silk, 1968; Sakai, 1969; Peebles, 1980a). This need not be a problem, however, since with sufficient care fictitious "gauge mode" solutions may be eliminated (Press and Vishniac, 1980a). An independent and interesting approach to the problem has recently been presented by Bardeen (1980). Following earlier work of Hawking (1966) and Olson (1976), Bardeen discusses a formalism in which the time development of gauge-invariant measures of small perturbations to the homogeneous background may be followed.

We shall discuss the case of a scalar (i.e. density) plane-wave perturbation (Lifshitz and Khalatnikov, 1963), in which

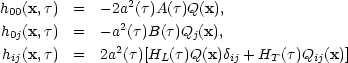(3.9a) (3.9b) (3.9c)

where

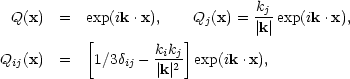(3.10)

and k is the comoving wave vector. The four-velocity may be written,

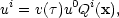(3.11a)

with

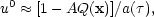(3.11b)

where (3.11b) results from the normalization condition u_µu^µ = - 1. The perturbed energy-momentum tensor may be written,

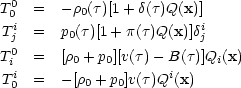(3.12a) (3.12b) (3.12c) (3.12d)

We can now investigate the way in which the perturbation amplitudes in Eqs. (3.8)-(3.11) change under a coordinate transformation. Since the perturbation analysis is only to first order, only the first order effects of the transformation need be considered. The most general coordinate transformation may be written [Eq. (3.7)],

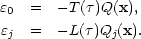(3.13a) (3.13b)

Hence the perturbation amplitudes transform as (Weinberg, 1972, Section 10.9; Bardeen, 1980),

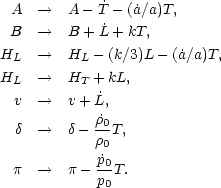(3.14a) (3.14b) (3.14c (3.14d) (3.14e) (3.14f) (3.14g)

The amplitudes in Eqs. (3.14) may be combined to produce gauge invariant amplitudes. For example, one of the quantities considered by Bardeen,

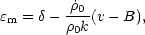(3.15)

is clearly gauge invariant by Eqs. (3.14b, e, f). The quantity _m is equal to in a gauge in which v = B, i.e. if the matter worldlines are orthogonal to the hypersurface of constant time . Even in a gauge-invariant formalism there remains some ambiguity since one can define various gauge-invariant quantities like _m which may be interpreted as by some appropriate choice of hypersurface of simultaneity. In practice, for a sensible choice of hypersurface, the ambiguity disappears once the perturbation is well within the horizon, hence _m for k >> 1. The motivation behind Bardeen's discussion of _m is that the equations governing its time evolution are particularly simple.

If the entropy per baryon is constant (adiabatic fluctuations), then [Eqs. (3.5)]

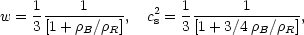(3.16)

and w = c_s² . It is also interesting to include "entropy" perturbations, i.e. _R / _R 4/3 _B / _B. This may be done by considering the amplitude.

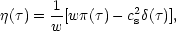(3.17)

which is gauge invariant by Eqs. (3.14f, g). Bardeen derives the equation governing the time evolution of _m which, in the radiation era when w c_s² 1/3 takes the simple form,

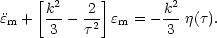(3.18)

Ignoring the source term (), it can be seen that the solutions to Eq. (3.18) will show oscillatory behavior on scales smaller than the horizon (k >> 1) _m exp(ik / 3^1/2) and power law behaviour, _m = f_g ² + f_d ^-1 on scales greater than the horizon. These results agree with those obtained by Sakai (1969) using the comoving gauge (uⁱ = h_0i = 0) but differ from the growth rates obtained using the synchronous gauge (h₀₀ = h_0i = 0, Weinberg, 1972; Peebles, 1980a; Press and Vishniac, 1980a). These authors find solutions, = fg₁ ² + fg₂ + f_d ^-2 for perturbations with k << 1. The decaying mode f_d ^-2 has no physical significance since it may be eliminated by adjusting the initial hyper-surface of constant time (see Press and Vishniac). On scales smaller than the horizon, the synchronous gauge gives exp[ik / 3^1/2] which agrees with the behaviour of _m for k >> 1.

Now consider the term (), this acts as a source term in Eq. (3.18) and one might speculate that a non-zero () might generate fluctuations in _m. Consider for example, the case in which some of the matter is suddenly converted into a pressureless form, perhaps black holes. This will generate a pressure inhomogeneity (Meszaros, 1975: Carr, 1977),

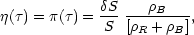(3.19)

but we can see from Eq. (3.18) that the induced _m will be of order ~ k^{2 2} () and is due to pressure gradients transmitted at the sound speed. Thus if the perturbation comes within the horizon during the radiation era, _m (). This result is discussed in more detail by Press and Vishniac (1980a) who show that it is also true for perturbations which enter the horizon during the matter-dominated era, and by Bardeen (1980) who also considers the possible role of anisotropic stress perturbations. Their results lead to an important conclusion concerning the possibility of spontaneously forming density perturbations at early times which we discuss below.

⁶ Here, Greek indices run from 0 to 3 whilst Latin indices run from 1 to 3 and covariant derivatives will be denoted by a semi-colon. Units are chosen so that c = 1. Back.