1.2. Phase transitions and finite temperature field theory

Phase transitions are known to occur in the early universe. Examples we mentioned are the quark to hadron (confinement) transition, which QCD predicts at an energy around 1 GeV, and the electroweak phase transition at about 250 GeV. Within grand unified theories (GUT), aiming to describe the physics beyond the standard model, other phase transitions are predicted to occur at energies of order 10¹⁵ GeV; during these, the Higgs field tends to fall towards the minima of its potential while the overall temperature of the universe decreases as a consequence of the expansion.

A familiar theory to make a bit more quantitative the above considerations is the ||⁴ theory,

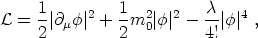
(1)

with m²₀ > 0. The second and third terms on the right hand side yield the usual `Mexican hat' potential for the complex scalar field. For energies much larger than the critical temperature, T<sub>c</sub>, the fields are in the so-called `false' vacuum: a highly symmetric state characterized by a vacuum expectation value <| | > = 0. But when energies decrease the symmetry is spontaneously broken: a new `true' vacuum develops and the scalar field rolls down the potential and sits onto one of the degenerate new minima. In this situation the vacuum expectation value becomes <| | >² = 6 m₀² / .

Research done in the 1970's in finite-temperature field theory [Weinberg, 1974; Dolan & Jackiw, 1974; Kirzhnits & Linde, 1974] has led to the result that the temperature-dependent effective potential can be written down as

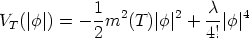
(2)

with T_c² = 24 m₀² / , m²(T) = m₀² (1 - T² / T_c²), and <| | >² = 6 m²(T) / . We easily see that when T approaches T_c from below the symmetry is restored, and again we have <| | > = 0. In condensed-matter jargon, the transition described above is second-order [Mermin, 1979]. ⁽³⁾

³ In a first-order phase transition the order parameter (e.g., < | | > in our case) is not continuous. It may proceed by bubble nucleation [Callan & Coleman, 1977; Linde, 1983b] or by spinoidal decomposition [Langer, 1992]. Phase transitions can also be continuous second-order processes. The `order' depends sensitively on the ratio of the coupling constants appearing in the Lagrangian. Back.